
题目列表(包括答案和解析)
11. (山东卷)已知x和y是正整数,且满足约束条件
(山东卷)已知x和y是正整数,且满足约束条件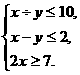 则x-2x
则x-2x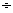 3y的最小值是
3y的最小值是
(A)24 (B)14 (C)13 (D)11.5
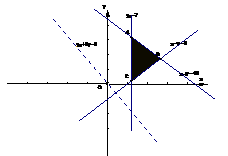
解:画出可域:如图所示易得
B点坐标为(6,4)且当直线z=2x+3y
过点B时z取最大值,此时z=24,点
C的坐标为(3.5,1.5),过点C时取得最小值,
但x,y都是整数,最接近的整数解为(4,2),
故所求的最小值为14,选B
10. (山东卷)某公司招收男职员x名,女职员y名,x和y须满足约束条件
(山东卷)某公司招收男职员x名,女职员y名,x和y须满足约束条件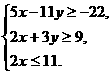 则z=10x+10y的最大值是
则z=10x+10y的最大值是
(A)80 (B) 85 (C) 90 (D)95
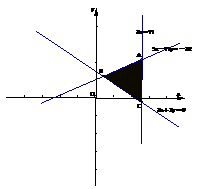
解:画出可行域:
易得A(5.5,4.5)且当直线z=10x+10y过A点时,
z取得最大值,此时z=90,选C
9.(全国卷I)从圆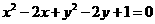 外一点
外一点 向这个圆作两条切线,则两切线夹角的余弦值为
向这个圆作两条切线,则两切线夹角的余弦值为
A.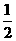 B.
B.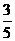 C.
C.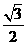 D.
D.
解析:圆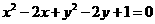 的圆心为M(1,1),半径为1,从外一点
的圆心为M(1,1),半径为1,从外一点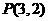 向这个圆作两条切线,则点P到圆心M的距离等于
向这个圆作两条切线,则点P到圆心M的距离等于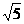 ,每条切线与PM的夹角的正切值等于
,每条切线与PM的夹角的正切值等于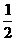 ,所以两切线夹角的正切值为
,所以两切线夹角的正切值为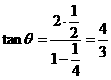 ,该角的余弦值等于
,该角的余弦值等于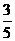 ,选B.
,选B.
8.(江苏卷)圆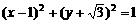 的切线方程中有一个是
的切线方程中有一个是
(A)x-y=0 (B)x+y=0 (C)x=0 (D)y=0
[正确解答]直线ax+by=0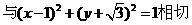 ,则
,则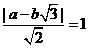 ,由排除法,
,由排除法,
选C,本题也可数形结合,画出他们的图象自然会选C,用图象法解最省事。
[解后反思]直线与圆相切可以有两种方式转化(1)几何条件:圆心到直线的距离等于半径(2)代数条件:直线与圆的方程组成方程组有唯一解,从而转化成判别式等于零来解.
7.(湖南卷)圆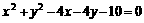 上的点到直线
上的点到直线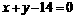 的最大距离与最小距离的差是
的最大距离与最小距离的差是
A.36
B. 18 C.  D.
D. 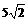
解析:圆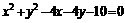 的圆心为(2,2),半径为3
的圆心为(2,2),半径为3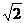 ,圆心到直线
,圆心到直线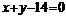 的距离为
的距离为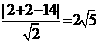 >3
>3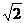 ,圆上的点到直线的最大距离与最小距离的差是2R =6
,圆上的点到直线的最大距离与最小距离的差是2R =6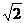 ,选C.
,选C.
6.(湖南卷)若圆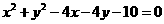 上至少有三个不同点到直线
上至少有三个不同点到直线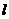 :
: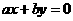 的距离为
的距离为 ,则直线
,则直线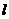 的倾斜角的取值范围是 ( )
的倾斜角的取值范围是 ( )
A.[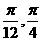 ]
B.[
]
B.[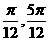 ]
C.[
]
C.[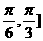 D.
D.
解析:圆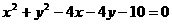 整理为
整理为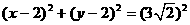 ,∴圆心坐标为(2,2),半径为3
,∴圆心坐标为(2,2),半径为3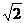 ,要求圆上至少有三个不同的点到直线
,要求圆上至少有三个不同的点到直线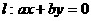 的距离为
的距离为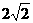 ,则圆心到直线的距离应小于等于
,则圆心到直线的距离应小于等于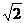 , ∴
, ∴ 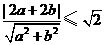 ,∴
,∴ 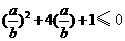 ,∴
,∴ 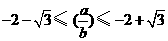 ,
,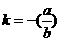 ,∴
,∴ 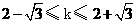 ,直线
,直线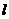 的倾斜角的取值范围是
的倾斜角的取值范围是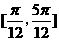 ,选B.
,选B.
5.(湖北卷)已知平面区域D由以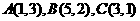 为顶点的三角形内部&边界组成。若在区域D上有无穷多个点
为顶点的三角形内部&边界组成。若在区域D上有无穷多个点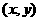 可使目标函数z=x+my取得最小值,则
可使目标函数z=x+my取得最小值,则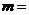
A.-2 B.-1 C.1 D.4
解:依题意,令z=0,可得直线x+my=0的斜率为- ,结合可行域可知当直线x+my=0与直线AC平行时,线段AC上的任意一点都可使目标函数z=x+my取得最小值,而直线AC的斜率为-1,所以m=1,选C
,结合可行域可知当直线x+my=0与直线AC平行时,线段AC上的任意一点都可使目标函数z=x+my取得最小值,而直线AC的斜率为-1,所以m=1,选C
4.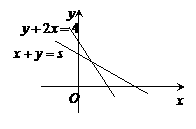 (广东卷)在约束条件
(广东卷)在约束条件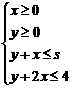 下,当
下,当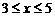 时,目标函数
时,目标函数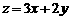 的最大值的变化范围是
的最大值的变化范围是
A.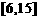 B.
B. 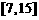 C.
C. 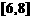 D.
D. 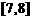
解析:由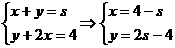 交点为
交点为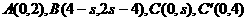 ,
,
(1)当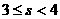 时可行域是四边形OABC,此时,
时可行域是四边形OABC,此时,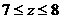 (2)当
(2)当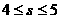 时可行域是△OA
时可行域是△OA 此时,
此时,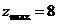 ,故选D.
,故选D.
3.(福建卷)已知两条直线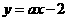 和
和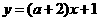 互相垂直,则
互相垂直,则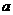 等于
等于
(A)2 (B)1 (C)0 (D)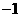
解析:两条直线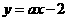 和
和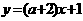 互相垂直,则
互相垂直,则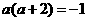 ,∴ a=-1,选D.
,∴ a=-1,选D.
2.(安徽卷)直线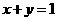 与圆
与圆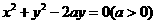 没有公共点,则
没有公共点,则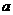 的取值范围是
的取值范围是
A.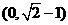 B.
B.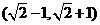 C.
C.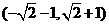 D.
D.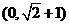
解:由圆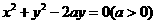 的圆心
的圆心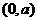 到直线
到直线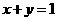 大于
大于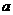 ,且
,且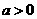 ,选A。
,选A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com