
题目列表(包括答案和解析)
42.(上海卷)求函数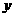 =2
=2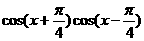 +
+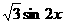 的值域和最小正周期.
的值域和最小正周期.
[解] 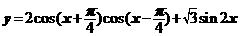
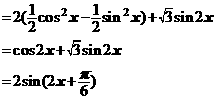
∴ 函数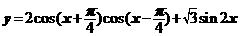 的值域是
的值域是 ,最小正周期是
,最小正周期是 ;
;
40.(山东卷)已知函数f(x)=A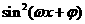 (A>0,
(A>0, >0,0<
>0,0<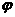 <
<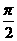 函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求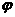 ;
;
(2)计算f(1)+f(2)+… +f(2 008).
解:(I)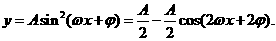
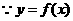 的最大值为2,
的最大值为2,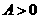 .
.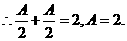
又 其图象相邻两对称轴间的距离为2,
其图象相邻两对称轴间的距离为2, ,
,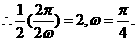
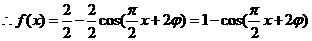 .
.
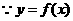 过
过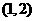 点,
点,
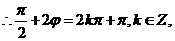
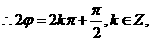
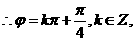
又
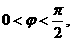
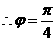 .
.
(II)解法一: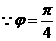 ,
,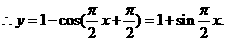
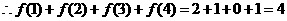 .
.
又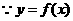 的周期为4,
的周期为4,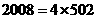 ,
,
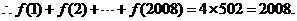
解法二: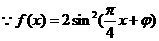
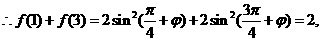
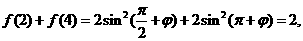
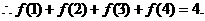
又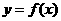 的周期为4,
的周期为4,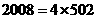 ,
,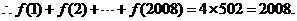
41(陕西卷)已知函数f(x)=sin(2x-)+2sin2(x-) (x∈R)
(Ⅰ)求函数f(x)的最小正周期 ; (2)求使函数f(x)取得最大值的x的集合.
解:(Ⅰ) f(x)=sin(2x-)+1-cos2(x-)
= 2[sin2(x-)- cos2(x-)]+1
=2sin[2(x-)-]+1
= 2sin(2x-) +1
∴ T==π
(Ⅱ)当f(x)取最大值时, sin(2x-)=1,有 2x- =2kπ+
即x=kπ+ (k∈Z) ∴所求x的集合为{x∈R|x= kπ+ , (k∈Z)}.
39.(辽宁卷)已知函数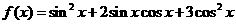 ,
,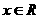 .求:
.求:
(I) 函数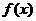 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量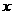 的集合;
的集合;
(II) 函数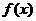 的单调增区间.
的单调增区间.
[解析](I) 解法一:

 当
当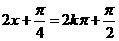 ,即
,即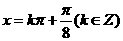 时,
时, 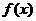 取得最大值
取得最大值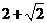 .
.
函数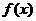 的取得最大值的自变量
的取得最大值的自变量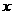 的集合为
的集合为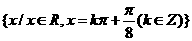 .
.
解法二:
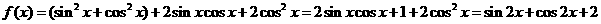
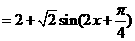
 当
当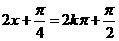 ,即
,即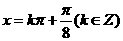 时,
时, 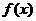 取得最大值
取得最大值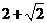 .
.
函数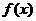 的取得最大值的自变量
的取得最大值的自变量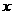 的集合为
的集合为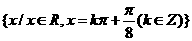 .
.
(II)解: 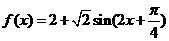 由题意得:
由题意得: 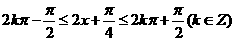
即: 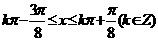 因此函数
因此函数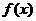 的单调增区间为
的单调增区间为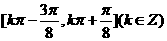 .
.
[点评]本小题考查三角公式,三角函数的性质及已知三角函数值求角等基础知识,考查综合运用三角有关知识的能力.
38.(湖南卷)已知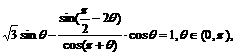 求θ的值.
求θ的值.
解析: 由已知条件得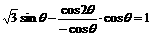 .
.
即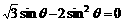 .
.
解得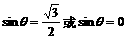 .
.
由0<θ<π知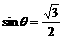 ,从而
,从而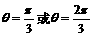 .
.
37.(广东卷)已知函数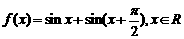 .
.
(I)求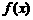 的最小正周期;
的最小正周期;
(II)求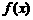 的的最大值和最小值;
的的最大值和最小值;
(III)若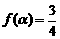 ,求
,求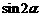 的值.
的值.
解: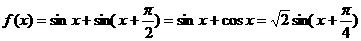
(Ⅰ)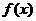 的最小正周期为
的最小正周期为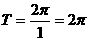 ;
;
(Ⅱ)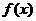 的最大值为
的最大值为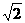 和最小值
和最小值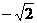 ;
;
(Ⅲ)因为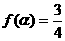 ,即
,即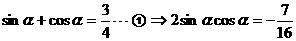 ,即
,即 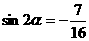
36.(福建卷)已知函数f(x)=sin2x+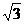 xcosx+2cos2x,x
xcosx+2cos2x,x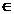 R.
R.
(I)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
本小题主要考查三角函数的基本公式、三角恒等变换、三角函数的图象和性质等基本知识,以及推理和运算能力。满分12分。
解:(I)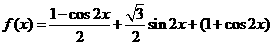
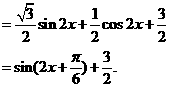
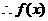 的最小正周期
的最小正周期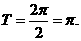
由题意得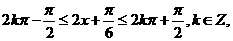 即
即 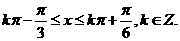
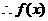 的单调增区间为
的单调增区间为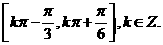
(II)方法一: 先把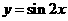 图象上所有点向左平移
图象上所有点向左平移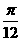 个单位长度,得到
个单位长度,得到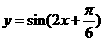 的图象,再把所得图象上所有的点向上平移
的图象,再把所得图象上所有的点向上平移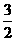 个单位长度,就得到
个单位长度,就得到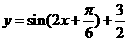 的图象。
的图象。
方法二:把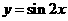 图象上所有的点按向量
图象上所有的点按向量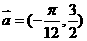 平移,就得到
平移,就得到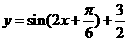 的图象。
的图象。
35.(北京卷)已知函数f(x)=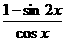 (Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan
(Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tan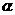 =
=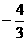 ,求f(
,求f(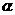 )的值.
)的值.
解:(Ⅰ)由cosx≠0得x≠kπ+ (k∈Z),
故f(x)的定义域为{|x|x≠kπ+
(k∈Z),
故f(x)的定义域为{|x|x≠kπ+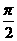 ,k∈Z}.
(Ⅱ)因为tanα=
,k∈Z}.
(Ⅱ)因为tanα=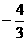 ,且α是第四象限的角, 所以sinα=
,且α是第四象限的角, 所以sinα=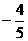 ,cosα=
,cosα=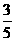 ,
,
故f(α)=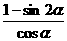 =
=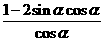 =
=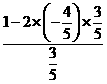 =
=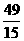 .
.
34.(北京卷)已知函数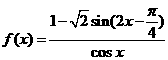 ,
,
(Ⅰ)求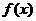 的定义域;
的定义域;
(Ⅱ)设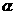 是第四象限的角,且
是第四象限的角,且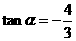 ,求
,求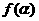 的值.
的值.
解:(1)依题意,有cosx¹0,解得x¹kp+ ,
,
即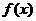 的定义域为{x|xÎR,且x¹kp+
的定义域为{x|xÎR,且x¹kp+ ,kÎZ}
,kÎZ}
(2)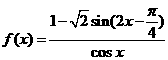 =-2sinx+2cosx\
=-2sinx+2cosx\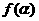 =-2sina+2cosa
=-2sina+2cosa
由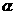 是第四象限的角,且
是第四象限的角,且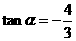 可得sina=-
可得sina=-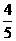 ,cosa=
,cosa=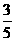
\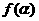 =-2sina+2cosa=
=-2sina+2cosa=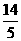
33.(安徽卷)已知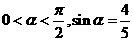
(Ⅰ)求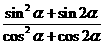 的值;
的值;
(Ⅱ)求 的值。
的值。
解:(Ⅰ)由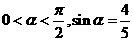 ,得
,得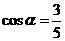 ,所以
,所以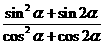 =
=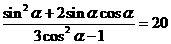 。
。
(Ⅱ)∵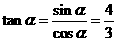 ,∴
,∴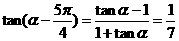 。
。
32.(安徽卷)已知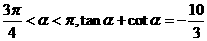
(Ⅰ)求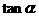 的值;
的值;
(Ⅱ)求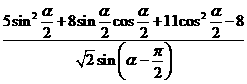 的值。
的值。
解:(Ⅰ)由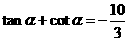 得
得 ,即
,即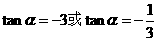 ,又
,又 ,所以
,所以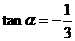 为所求。
为所求。
(Ⅱ)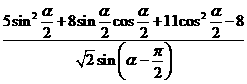 =
=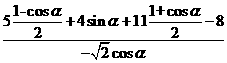
=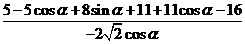 =
=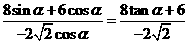 =
=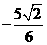 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com