
题目列表(包括答案和解析)
21.(本小题满分12分)
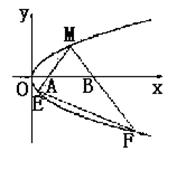 如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程.
[思路点拨]本题涉及抛物线与直线相交的有关知识.
[正确解答](1)设M(y ,y0),直线ME的斜率为k(l>0)
,y0),直线ME的斜率为k(l>0)
则直线MF的斜率为-k,

 消
消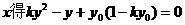
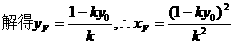
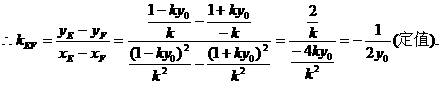
所以直线EF的斜率为定值
(2)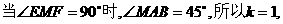

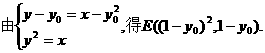
同理可得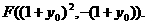
设重心G(x, y),则有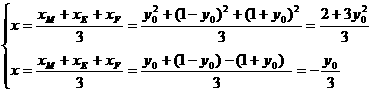
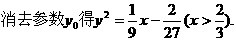
[解后反思]这是一道重要的数学问题,它属于解析几何范畴,几乎是高考数学每年的必考内容之一,此类问题一定要”大胆假设,细心求解”,根据题目要求先将题目所涉及的未知量都可以设出来,然后根据题目把所有的条件都变成等式,一定可以求出来,当然求的过程中,采取适当的小技巧,例如化简或适当分类讨论,可以大为简化过程,而且会尽量多多得分,同时这一类题目也需要很强的计算能力.
20.(本小题满分12分)
如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
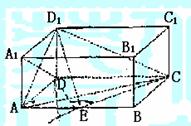 (1)证明:D1E⊥A1D;
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为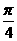 .
.
见理科卷20.
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.
[思路点拨]本题涉及随机事件的有关概率.
[正确解答]设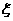 表示游戏终止时掷硬币的次数,
表示游戏终止时掷硬币的次数,
设正面出现的次数为m,反面出现的次数为n,则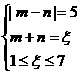 ,可得:
,可得:
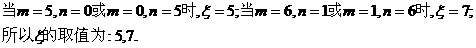
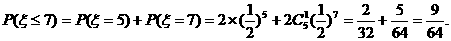
[解后反思]这是一道比较复杂的概率题目,首先我们应理解随机变量及其概率分布的概念,掌握分布函数F(x)= P{X≤x}的概念及性质;才能会计算与随机变量相关的事件的概率.同时我们在解决的过程中,也适当对此类解题的流程也要有一个清晰的了解,这样才能保证此类题目得高分和全分.
18.(本小题满分12分)
已知向量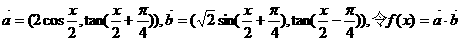 .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
[思路点拨]本题主要考查向量与三角函数的综合题,正确求出f(x)是解该题的关键.
[正确解答]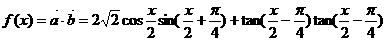
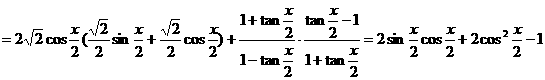
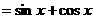 =
=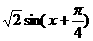 .
.
所以 ,最小正周期为
,最小正周期为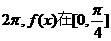 上单调增加,
上单调增加,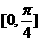 上单调减少.
上单调减少.
[解后反思]这是一道向量与三角函数的综合题,向量虽然是近年高中数学出现的新知识,但向量知识却很重要.因为向量是近代数学中重要和基本的数学概念之一,它是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景.在学习过程中,同学将会了解向量丰富的实际背景,逐渐理解平面向量及其运算的意义,一定能要用向量语言和方法表述和解决数学和物理中的一些问题,发展数学运算能力和解决数学实际问题的能力.
17.(本小题满分12分)
已知函数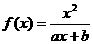 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;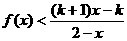 .
.
见理科卷17.
16.以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,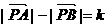 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若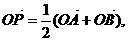 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程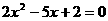 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
见理科卷16.
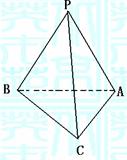
15.如图,在三棱锥P-ABC中,PA=PB=PC=BC,
且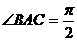 ,则PA与底面ABC所成角为
,则PA与底面ABC所成角为
.
[思路点拨]本题主要考查直线与平面所成的角的求法,关键是
确定点P在底面的射影O的位置.
[正确解答]过P作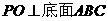 ,交底面于O,连结AO并延长交BC于D,连结PD,则PD、AD均垂直于BC,所以AB=AC,PA与底面ABC所成角为
,交底面于O,连结AO并延长交BC于D,连结PD,则PD、AD均垂直于BC,所以AB=AC,PA与底面ABC所成角为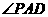 ,
,
设AC=1,则PA=PB=PC=BC=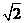 ,
, ,
,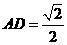 ,
,
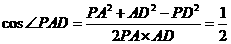 ,所以
,所以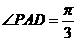 .
.
[解后反思]熟练掌握三角形的“四心”是快速解该题的关键.外心:三角形三条中垂线的交点,性质外心到三角顶点距离相等,内心:内角平分线的交点,性质是内心到三边距离相等,垂心:三条高线的交点,重心:三条中线的交点,另外记住一些结论也是大有裨益的,比如在三棱锥P-ABC中(1)若P到三个顶点的距离相等,则P在底面的射影是 ABC的外心,(2)若P到三边的距离相等,则P在底面的射影是
ABC的外心,(2)若P到三边的距离相等,则P在底面的射影是 的内心,(3)若
的内心,(3)若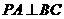
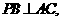 则
则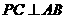 且P在底面的射影是
且P在底面的射影是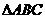 的垂心.
的垂心.
14.设实数x, y满足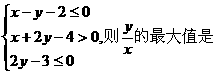 .
.
见理科卷14
13.若函数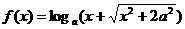 是奇函数,则a=
.
是奇函数,则a=
.
 见理科卷13
见理科卷13
11.在△OAB中,O为坐标原点,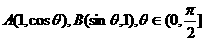 ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,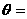 ( )
( )
A.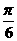 B.
B.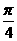 C.
C.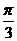 D.
D.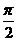
见理科卷11
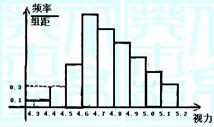 12.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
12.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
A.0,27,78 B.0,27,83 C.2.7,78 D.2.7,83
[思路点拨]本题涉及数理统计的若干知识.
[正确解答]由图象可知,前4组的公比为3,最大频率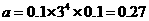 ,设后六组公差为
,设后六组公差为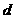 ,则
,则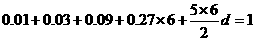 ,解得:
,解得: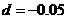 ,
,
后四组公差为-0.05, 所以,视力在4.6到5.0之间的学生数为(0.27+0.22+0.17+0.12)×100=78(人).选A.
[解后反思]本题是一道数理统计图象题,关于统计一般可分为三步,第一步抽样,第二步根据抽样所得结果,画成图形,第三步根据图形,分析结论.本题是统计的第二步,在此类问题中,可画成两种图形,一个是频率分布直方图,另一个是频率分布条形图,两者有很大的不同,前者是以面积表示频数,频率分布条形图是以高度表示频数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com