
题目列表(包括答案和解析)
12.将1,2,…,9这9个数平均分成三组,则每组的三个数都成等差数列的概率为( )
A.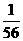 B.
B.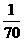 C.
C.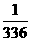 D.
D.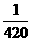
[思路点拨]本题主要考查平均分组问题及概率问题.
[正确解答]将1,22-------9平均分成三组的数目为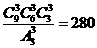 ,又每组的三个数成等差数列,种数为了4,所以答案为B
,又每组的三个数成等差数列,种数为了4,所以答案为B
[解后反思]这是一道概率题,属于等可能事件,在求的过程中,先求出不加条件限制的所有可能性a,然后再根据条件,求出满足题目要求的可能种数b,最后要求的概率就是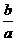 .
.
11.在△OAB中,O为坐标原点,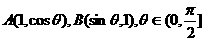 ,则△OAB的面积达到最大值时,
,则△OAB的面积达到最大值时,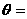 ( )
( )
A.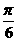 B.
B.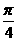 C.
C.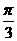 D.
D.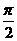
[思路点拨]运用图形,根据图形表示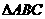 的面积,将实际问题转化成数学问题.
的面积,将实际问题转化成数学问题.
[正确解答]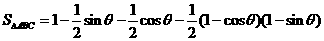
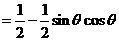
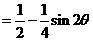
当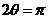 即
即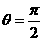 时,面积最大.
时,面积最大.
[解后反思]运用三角函数解决相应的实际问题,首先应根据题目的要求将面积的表达式写出来,然后在表达式中,根据自变量的取值范围,最终求出答案,所要注意的是,解决此类问题时不能仅凭函数的表达式,应考虑实际情况,例如,在函数的自变量中,可以取负数,而如果在实际题目中,自变量表示的是天数,那么这相自变量必须为正数,且为整数等等.
10.已知实数a,
b满足等式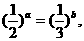 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
[思路点拨]本题涉及指数函数的若干知识.
[正确解答]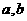 均大于零时,要满足等式,必有
均大于零时,要满足等式,必有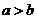 ;
;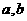 均小于零时,要满足等式,必有
均小于零时,要满足等式,必有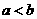 ;
;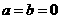 时,显然等式成立.因此不可能成立的关系式为③④,选B
时,显然等式成立.因此不可能成立的关系式为③④,选B
[解后反思]根据函数图形来解客观题,快速而且准确,这就要求对函数的图形要相当了解.
9.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为 ( )
A.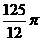 B.
B.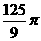 C.
C.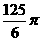 D.
D.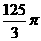
[思路点拨]本题主要考查图形的翻折问题,利用球心到球面的距离均相等,找出球心是解本题的关健.
[正确解答]连接矩形ABCD的对角线AC、BD交于O,则AO=BO=CO=DO,则O为四面体ABCD的外接球的圆心,因此四面体ABCD的外接球的半径为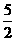 ,体积为
,体积为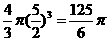 .选C.
.选C.
[解后反思]对于图形的翻折问题,关健是利用翻折前后的不变量,另外,球和正方体,长方体,三棱锥的组合问题,应引起高度重视,而且有些问题也可以通过补形法转化成球内接正方体或内接长方体问题.
8.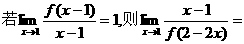 ( )
( )
A.-1 B.1 C.-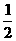 D.
D.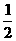
[思路点拨]本题主要是考查函数极限法则的运用,涉及函数在某一点的极限的有关知识.
[正确解答]令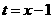 ,则
,则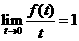 ,令
,令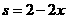 ,则
,则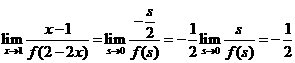 .选C.
.选C.
[解后反思]本题首先利用整体代换的方法,简化极限运算中式子,然后使用配凑法,将最值式子进行简化,再将简化后的条件代入因式,得出解.在做这一类题目时,先适当的将条件化简是解决的关健.
7.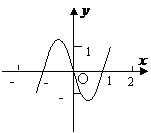 已知函数
已知函数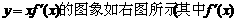
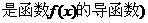 ,下面四个图象中
,下面四个图象中
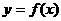 的图象大致是 ( )
的图象大致是 ( )
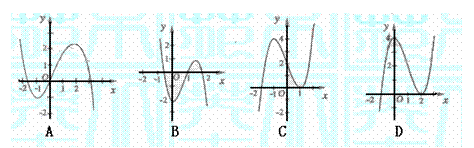
[思路点拨]本题考查导函数的图象及其性质,由图象得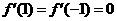 ,从而导出
,从而导出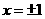 是函数f(x)极值点是解本题的关健.
是函数f(x)极值点是解本题的关健.
[正确解答]由图象知,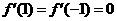 ,所以
,所以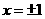 是函数
是函数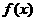 的极值点,又因为在
的极值点,又因为在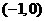 上,
上,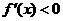 ,在
,在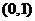 上,
上,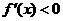 ,因此在
,因此在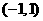 上,
上,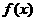 单调递减,故选C.
单调递减,故选C.
[解后反思]要注意,若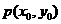 是函数y=f(x)的极值点,则有
是函数y=f(x)的极值点,则有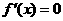 ,但是若
,但是若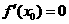 ,则是
,则是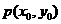 不一定是函数y=f(x)极值点,所以要判断一个点是否为极值点,还要检验点
不一定是函数y=f(x)极值点,所以要判断一个点是否为极值点,还要检验点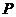 的两侧的单调性是否不同.
的两侧的单调性是否不同.
6.已知向量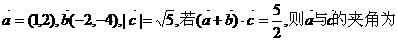 ( )
( )
A.30° B.60°
C.120° D.150°
[思路点拨]本题考查平面向量的运算及向量的夹角公式.
[正确解答]设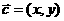 ,则
,则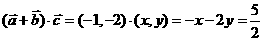 ,又
,又
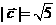 ,所以
,所以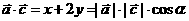 ,得
,得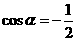 ,
,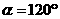 ,
,
选C.
[解后反思]设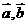 的夹角为
的夹角为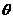 ,则
,则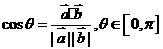 ,(1)当
,(1)当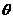 为锐角,有
为锐角,有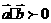 且
且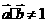 (2) 当
(2) 当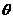 为钝角,有
为钝角,有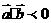 且
且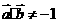 (3)当
(3)当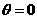 ,
,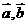 共线且方向相同.(4)当
共线且方向相同.(4)当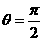 时,
时, 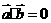 .
.
5.设函数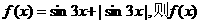 为 ( )
为 ( )
A.周期函数,最小正周期为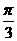 B.周期函数,最小正周期为
B.周期函数,最小正周期为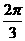
C.周期函数,数小正周期为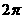 D.非周期函数
D.非周期函数
[思路点拨]本题考查三角函数的周期,首先应将f(x)化简,尽可能地化成形如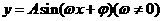 然后再判断.
然后再判断.
[正确解答]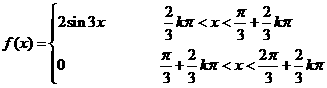
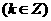 ,
,
因此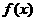 为周期函数,且最小正周期为
为周期函数,且最小正周期为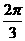 .选B.
.选B.
[解后反思]本题也可根据三角函数周期定义进行检验,将A、
B 、C 、D中的周期都代入,验证后,可得答案B,另外记住一些常用结论是必要的,例如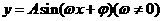 的最小正周期
的最小正周期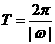 ,
,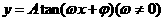 最小正周期
最小正周期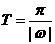 .
.
4.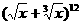 的展开式中,含x的正整数次幂的项共有 ( )
的展开式中,含x的正整数次幂的项共有 ( )
A.4项 B.3项 C.2项 D.1项
[思路点拨]本题主要考查二项式展开通项公式的有关知识.
[正确解答]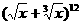 的展开式为
的展开式为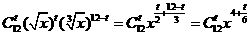 ,因此含x的正整数次幂的项共有3项.选B
,因此含x的正整数次幂的项共有3项.选B
[解后反思]在二项式展开式中,要注意二项式定理的变形,要掌握二项展开式中的系数与二项式系数的区别.
3.
“a=b”是“直线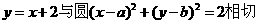 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
[思路点拨]本题主要考查直线和圆相切的条件以及充要条件,直线与圆相切的充要条件是
圆心到直线的距离等于半径.
[正确解答]直线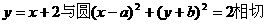 ,则
,则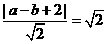 ,得
,得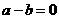 或
或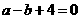 ,
,
因此“a=b”是“直线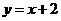 与圆
与圆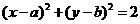 ”相切的充分不必要条件.
”相切的充分不必要条件.
选A
[解后反思]直线与圆相切可以有两种方式转化(1)几何条件:圆心到直线的距离等于半径(2)代数条件:直线与圆的方程组成方程组有唯一解,从而转化成判别式等于零来解,
A 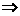 B,那么称A是B的充分条件,B是A的必要条件,但是实际问题中,我们往往是说B成立的的充分条件是A,千万不要搞错顺序.
B,那么称A是B的充分条件,B是A的必要条件,但是实际问题中,我们往往是说B成立的的充分条件是A,千万不要搞错顺序.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com