
题目列表(包括答案和解析)
2、已知复数z满足(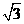 +3i)z=3i,则z=( )
+3i)z=3i,则z=( )
A.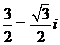 B.
B. 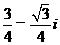 C.
C. 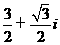 D.
D.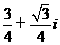
1、已知集合M={x|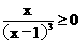 },N={y|y=3x2+1,xÎR},则MÇN=( )
},N={y|y=3x2+1,xÎR},则MÇN=( )
A.Æ B. {x|x³1} C.{x|x>1} D. {x| x³1或x<0}
20.本小题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题、解决问题的能力。
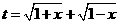
要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴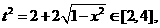 t≥0
①
t≥0
①
t的取值范围是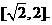 由①得
由①得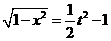
∴m(t)=a(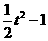 )+t=
)+t=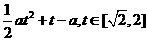
(2)由题意知g(a)即为函数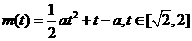 的最大值。
的最大值。
注意到直线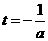 是抛物线
是抛物线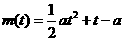 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
当a>0时,函数y=m(t), 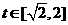 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由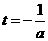 <0知m(t)在
<0知m(t)在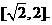 上单调递增,∴g(a)=m(2)=a+2
上单调递增,∴g(a)=m(2)=a+2
(2)当a=0时,m(t)=t, 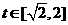 ,∴g(a)=2.
,∴g(a)=2.
(3)当a<0时,函数y=m(t), 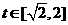 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若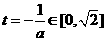 ,即
,即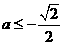 则
则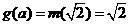
若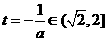 ,即
,即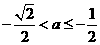 则
则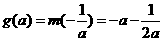
若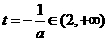 ,即
,即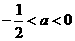 则
则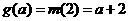
综上有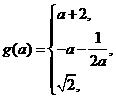
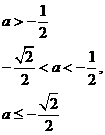
(3)解法一:
情形1:当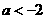 时
时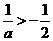 ,此时
,此时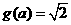 ,
,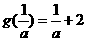
由 ,与a<-2矛盾。
,与a<-2矛盾。
情形2:当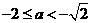
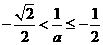 时,此时
时,此时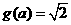 ,
,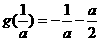
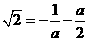 解得,
解得, 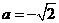 与
与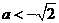 矛盾。
矛盾。
情形3:当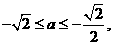
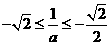 时,此时
时,此时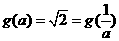
所以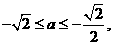
情形4:当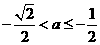 时,
时,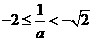 ,此时
,此时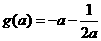 ,
,
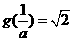
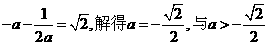 矛盾。
矛盾。
情形5:当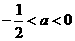 时,
时,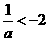 ,此时g(a)=a+2,
,此时g(a)=a+2,
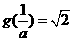
由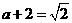 解得
解得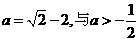 矛盾。
矛盾。
情形6:当a>0时,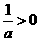 ,此时g(a)=a+2,
,此时g(a)=a+2, 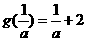
由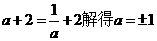 ,由a>0得a=1.
,由a>0得a=1.
综上知,满足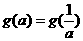 的所有实数a为
的所有实数a为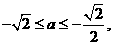 或a=1
或a=1
21本小题主要考查等差数列、充要条件等基础知识,考查综合运用数学知识分析问题、解决问题的能力。
证明:必要性,设是{an}公差为d1的等差数列,则
bn+1–bn=(an+1–an+3) – (an–an+2)= (an+1–an) – (an+3–an+2)= d1– d1=0
所以bn bn+1
( n=1,2,3,…)成立。
bn+1
( n=1,2,3,…)成立。
又cn+1–cn=(an+1–an)+2 (an+2–an+1)+3 (an+3–an+2)= d1+2 d1 +3d1 =6d1(常数) ( n=1,2,3,…)
所以数列{cn}为等差数列。
充分性:
设数列{cn}是公差为d2的等差数列,且bn bn+1
( n=1,2,3,…)
bn+1
( n=1,2,3,…)
∵cn=an+2an+1+3an+2 ①
∴cn+2=an+2+2an+3+3an+4 ②
①-②得cn–cn+2=(an–an+2)+2 (an+1–an+3)+3 (an+2–an+4)=bn+2bn+1+3bn+2
∵cn–cn+2=( cn–cn+1)+( cn+1–cn+2)= –2 d2
∴bn+2bn+1+3bn+2=–2 d2 ③
从而有bn+1+2bn+2+3bn+3=–2 d2 ④
④-③得(bn+1–bn)+2 (bn+2–bn+1)+3 (bn+3–bn+2)=0 ⑤
∵bn+1–bn≥0, bn+2–bn+1≥0 , bn+3–bn+2≥0,
∴由⑤得bn+1–bn=0 ( n=1,2,3,…),
由此不妨设bn=d3 ( n=1,2,3,…)则an–an+2= d3(常数).
由此cn=an+2an+1+3an+2= cn=4an+2an+1–3d3
从而cn+1=4an+1+2an+2–5d3 ,
两式相减得cn+1–cn=2( an+1–an) –2d3
因此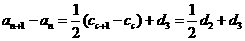 (常数) ( n=1,2,3,…)
(常数) ( n=1,2,3,…)
所以数列{an}公差等差数列。
[解后反思]理解公差d的涵义,能把文字叙述转化为符号关系式.利用递推关系是解决数列的重要方法,要求考生熟练掌握等差数列的定义、通项公式及其由来.
(17)(本小题满分12分,第一小问满分5分,第二小问满分7分)
已知三点P(5,2)、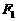 (-6,0)、
(-6,0)、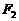 (6,0).
(6,0).
(Ⅰ)求以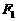 、
、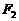 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
|
 (Ⅱ)设点P、
(Ⅱ)设点P、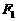 、
、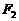 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为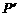 、
、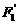 、
、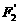 ,求以
,求以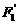 、
、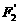 为焦点且过点
为焦点且过点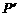 的双曲线的标准方程。
的双曲线的标准方程。
(18)(本小题满分14分)
|
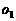 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
(19)(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
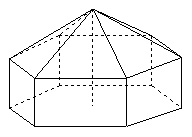
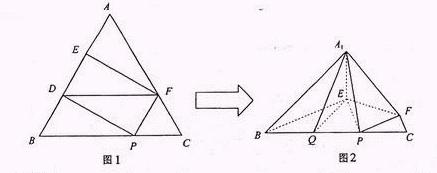
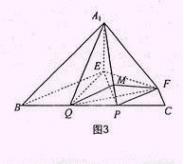
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到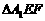 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)

(20)(本小题满分16分,第一小问4分,第二小问满分6分,第三小问满分6分)
设a为实数,设函数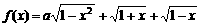 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=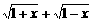 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足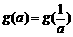 的所有实数a
的所有实数a
(21)(本小题满分14分)
设数列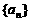 、
、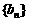 、
、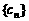 满足:
满足: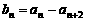 ,
,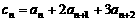 (n=1,2,3,…),
(n=1,2,3,…),
证明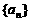 为等差数列的充分必要条件是
为等差数列的充分必要条件是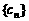 为等差数列且
为等差数列且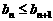 (n=1,2,3,…)
(n=1,2,3,…)

1[思路点拨]本题考查函数的奇偶性,三角函数sinx的奇偶性的判断,本题是一道送分的概念题
[正确解答]解法1由题意可知,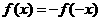 得a=0
得a=0
解法2:函数的定义域为R,又f(x)为奇函数,故其图象必过原点即f(0)=0,所以得a=0,
解法3由f(x)是奇函数图象法函数画出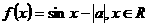 的图象选A
的图象选A
[解后反思]对数学概念及定理公式的深刻理解是解数学问题的关健,讨论函数的奇偶性,其前提条件是函数的定义域必须关于原点对称.
若函数f(x)为奇函数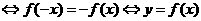 的图象关于原点对称.
的图象关于原点对称.
若函数f(x)为偶函数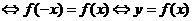 的图象关于y轴对称.
的图象关于y轴对称.
2[思路点拨]本题主要考查圆的切线的求法,直线与圆相切的充要条件是圆心到直线的距离等于半径.
[正确解答]直线ax+by=0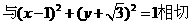 ,则
,则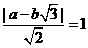 ,由排除法,
,由排除法,
选C,本题也可数形结合,画出他们的图象自然会选C,用图象法解最省事。
[解后反思]直线与圆相切可以有两种方式转化(1)几何条件:圆心到直线的距离等于半径(2)代数条件:直线与圆的方程组成方程组有唯一解,从而转化成判别式等于零来解.
3[思路点拨]本题考查统计的基本知识,样本平均数与样本方差的概念以及求解方程组的方法
[正确解答]由题意可得:x+y=20,(x-10)2+(y-10)2=8,解这个方程组需要用一些技巧,因为不要直接求出x、y,只要求出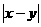 ,设x=10+t, y=10-t,
,设x=10+t, y=10-t, 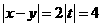 ,选D
,选D
[解后反思]
4[思路点拨]本题主要考三角函数的图象变换,这是一道平时训练的比较多的一种类型。
[正确解答]先将 的图象向左平移
的图象向左平移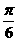 个单位长度,
个单位长度,
得到函数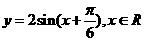 的图象,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数
的图象,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数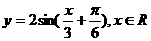 的图像
的图像
[解后反思]由函数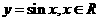 的图象经过变换得到函数
的图象经过变换得到函数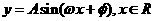
(1).y=Asinx,xÎR(A>0且A¹1)的图象可以看作把正弦曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的
(2)函数y=sinωx, xÎR (ω>0且ω¹1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的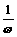 倍(纵坐标不变)
倍(纵坐标不变)
(3)函数y=sin(x+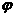 ),x∈R(其中
),x∈R(其中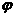 ≠0)的图象,可以看作把正弦曲线上所有点向左(当
≠0)的图象,可以看作把正弦曲线上所有点向左(当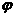 >0时)或向右(当
>0时)或向右(当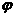 <0时=平行移动|
<0时=平行移动|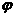 |个单位长度而得到
|个单位长度而得到 (用平移法注意讲清方向:“加左”“减右”)
(用平移法注意讲清方向:“加左”“减右”)
可以先平移变换后伸缩变换,也可以先伸缩变换后平移变换,但注意:先伸缩时,平移的单位把x前面的系数提取出来。
5[思路点拨]本题主要考查二项式展开通项公式的有关知识.
[正确解答]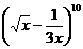 的展开式通项为
的展开式通项为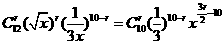 ,因此含x的正整数次幂的项共有2项.选B
,因此含x的正整数次幂的项共有2项.选B
[解后反思]多项式乘法的进位规则.在求系数过程中,尽量先化简,降底数的运算级别,尽量化成加减运算,在运算过程可以适当注意令值法的运用,例如求常数项,可令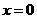 .在二项式的展开式中,要注意项的系数和二项式系数的区别.
.在二项式的展开式中,要注意项的系数和二项式系数的区别.
6[思路点拨]本题主要考查平面向量的数量积运算,抛物线的定义.
[正确解答]设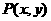 ,
,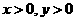 ,
,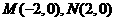 ,
,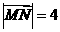
则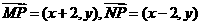
由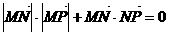 ,则
,则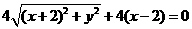 ,
,
化简整理得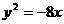 所以选B
所以选B
[解后反思]向量的坐标表示和数量积的性质在平面向量中的应用是学习的重点和难点.也是高考常常考查的重要内容之一.在平时请多多注意用坐标如何来表示向量平行和向量垂直,既要注意它们联系,也要注意它们的区别.
7[思路点拨]本题主要考查.集合的并集与交集运算,集合之间关系的理解。
[正确解答]因为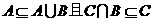
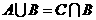 由题意得
由题意得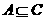 所以选A
所以选A
[解后反思]对集合的子、交、并、补运算,以及集合之间的关系要牢固掌握。本题考查三个抽象集合之间的关系,可以考虑借助与文氏图。
8[思路点拨]本题主要考查.不等式恒成立的条件,由于给出的是不完全提干,必须结合选择支,才能得出正确的结论。
[正确解答]运用排除法,C选项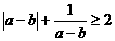 ,当a-b<0时不成立。
,当a-b<0时不成立。
[解后反思]运用公式一定要注意公式成立的条件
如果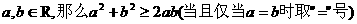
如果a,b是正数,那么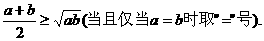
9[思路点拨]本题主要考查空间想象能力,以及正四棱锥的体积
[正确解答]由于两个正四棱锥相同,所以所求几何体的中心在正四棱锥底面正方形ABCD中心,有对称性知正四棱锥的高为正方体棱长的一半,影响几何体体积的只能是正四棱锥底面正方形ABCD的面积,问题转化为边长为1的正方形的内接正方形有多少种,所以选D.
[解后反思]正方体是大家熟悉的几何体,它的一些内接或外接图形需要一定的空间想象能力,要学会将空间问题向平面问题转化。
10[思路点拨]本题主要考查平均分组问题及概率问题.
[正确解答]将六个接线点随机地平均分成三组,共有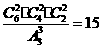 种结果,五个接收器能同时接收到信号必须全部在同一个串联线路中,有
种结果,五个接收器能同时接收到信号必须全部在同一个串联线路中,有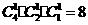 种结果,这五个接收器能同时接收到信号的概率是
种结果,这五个接收器能同时接收到信号的概率是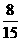 ,选D
,选D
[解后反思]概率问题的难点在于分析某事件所有可能出现的结果及其表示方法,而运用概率部分的性质、公式求某事件概率只是解决问题的工具而已
11[思路点拨]本题主要考查解三角形的基本知识
[正确解答]由正弦定理得,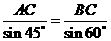 解得
解得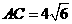
[解后反思]解三角形:已知两角及任一边运用正弦定理,已知两边及其夹角运用余弦定理
12[思路点拨]本题主要考查线性规划问题,由线性约束条件画出可行域,然后求出目标函数的最大值.
[正确解答]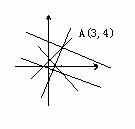 画出可行域,得在直线2x-y=2与直线x-y=-1的交点
画出可行域,得在直线2x-y=2与直线x-y=-1的交点
A(3,4)处,目标函数z最大值为18
[解后反思]本题只是直接考查线性规划问题,是一道较为简单的送分题。近年来高考线性规划问题高考数学考试的热点,数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法。 随着要求数学知识从书本到实际生活的呼声不断升高,线性规划这一类新型数学应用问题要引起重视。
13[思路点拨]本题考查排列组合的基本知识.
[正确解答]由题意可知,因同色球不加以区分,实际上是一个组合问题,共有
[解后反思]分步计数原理与分类计数原理是排列组合中解决问题的重要手段,也是基础方法,在高中数学中,只有这两个原理,尤其是分类计数原理与分类讨论有很多相通之处,当遇到比较复杂的问题时,用分类的方法可以有效的将之化简,达到求解的目的.
14[思路点拨]本题考查三角公式的记忆及熟练运用三角公式计算求值
[正确解答]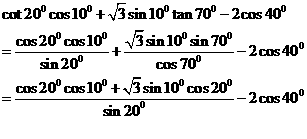
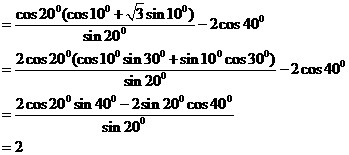
[解后反思]方法不拘泥,要注意灵活运用,在求三角的问题中,要注意这样的口决“三看”即(1)看角,把角尽量向特殊角或可计算角转化,(2)看名称,把一道等式尽量化成同一名称或相近的名称,例如把所有的切都转化为相应的弦,或把所有的弦转化为相应的切,(3)看式子,看式子是否满足三角函数的公式.如果满足直接使用,如果不满足转化一下角或转换一下名称,就可以使用.
15[思路点拨]本题考查应用导数求曲线切线的斜率,数列通项公式以及等比数列的前n项和的公式
[正确解答]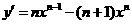 ,曲线y=xn(1-x)在x=2处的切线的斜率为k=n2n-1-(n+1)2n
,曲线y=xn(1-x)在x=2处的切线的斜率为k=n2n-1-(n+1)2n
切点为(2,-2n),所以切线方程为y+2n=k(x-2),令x=0得 an=(n+1)2n,令bn=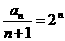 .数列
.数列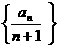 的前n项和为2+22+23+…+2n=2n+1-2
的前n项和为2+22+23+…+2n=2n+1-2
[解后反思]应用导数求曲线切线的斜率时,要首先判定所经过的点为切点。否则容易出错。
16[思路点拨]本题考查对数函数单调性和不等式的解法
[正确解答]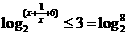 ,0〈
,0〈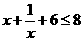 ,
,
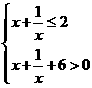 .
.
解得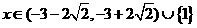
[解后反思]在数的比较大小过程中,要遵循这样的规律,异中求同即先将这些数的部分因式化成相同的部分,再去比较它们剩余部分,就会很轻易啦.一般在数的比较大小中有如下几种方法:(1)作差比较法和作商比较法,前者和零比较,后者和1比较大小;(2)找中间量,往往是1,在这些数中,有的比1大,有的比1小;,(3)计算所有数的值;(4)选用数形结合的方法,画出相应的图形;(5)利用函数的单调性等等.
17本小题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础知识和基本运算能力。
解:(1)由题意可设所求椭圆的标准方程为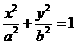 (a>b>0),其半焦距c=6
(a>b>0),其半焦距c=6
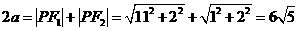 ∴
∴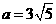 ,b2=a2-c2=9.
,b2=a2-c2=9.
所以所求椭圆的标准方程为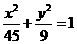
(2)点P(5,2)、F1(-6,0)、F2(6,0)关于直线y=x的对称点分别为点P,(2,5)、F1,(0,-6)、F2,(0,6).
设所求双曲线的标准方程为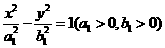 由题意知,半焦距c1=6
由题意知,半焦距c1=6
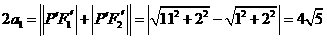
 ,b12=c12-a12=36-20=16. 所以所求双曲线的标准方程为
,b12=c12-a12=36-20=16. 所以所求双曲线的标准方程为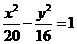
18.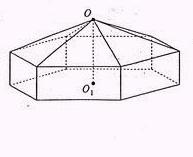 本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力。
本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力。
解:设OO1为x m,
则由题设可得正六棱锥底面边长为(单位:m)
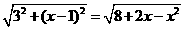
于是底面正六边形的面积为(单位:m2)
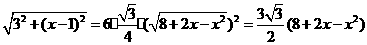
帐篷的体积为(单位:m3)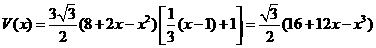
求导数,得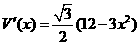
令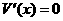 解得x=-2(不合题意,舍去),x=2.
解得x=-2(不合题意,舍去),x=2.
当1<x<2时,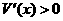 ,V(x)为增函数;
,V(x)为增函数;
当2<x<4时,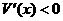 ,V(x)为减函数。
,V(x)为减函数。
所以当x=2时,V(x)最大。
答当OO1为2m时,帐篷的体积最大。
19本小题主要考查线面垂直、直线和平面所成的角、二面角等基础知识,以及空间线面位置关系的证明、角和距离的计算等,考查空间想象能力、逻辑推理能力和运算能力。
解法一:不妨设正三角形ABC的边长为3
(1)
在图1中,取BE中点D,连结DF. AE:EB=CF:FA=1:2∴AF=AD=2而∠A=600 , ∴△ADF是正三角形,又AE=DE=1, ∴EF⊥AD在图2中,A1E⊥EF, BE⊥EF, ∴∠A1EB为二面角A1-EF-B的平面角。由题设条件知此二面角为直二面角,A1E⊥BE,又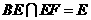 ∴A1E⊥平面BEF,即
A1E⊥平面BEP
∴A1E⊥平面BEF,即
A1E⊥平面BEP
(2) 在图2中,A1E不垂直A1B, ∴A1E是平面A1BP的垂线,又A1E⊥平面BEP,
 ∴A1E⊥BE.从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理)设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,则∠E1AQ就是A1E与平面A1BP所成的角,且BP⊥A1Q.在△EBP中, BE=EP=2而∠EBP=600 , ∴△EBP是等边三角形.又 A1E⊥平面BEP , ∴A1B=A1P, ∴Q为BP的中点,且
∴A1E⊥BE.从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理)设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,则∠E1AQ就是A1E与平面A1BP所成的角,且BP⊥A1Q.在△EBP中, BE=EP=2而∠EBP=600 , ∴△EBP是等边三角形.又 A1E⊥平面BEP , ∴A1B=A1P, ∴Q为BP的中点,且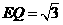 ,又 A1E=1,在Rt△A1EQ中,
,又 A1E=1,在Rt△A1EQ中,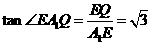 ,∴∠EA1Q=60o, ∴直线A1E与平面A1BP所成的角为600
,∴∠EA1Q=60o, ∴直线A1E与平面A1BP所成的角为600
在图3中,过F作FM⊥ A1P与M,连结QM,QF,∵CP=CF=1, ∠C=600,
∴△FCP是正三角形,∴PF=1.有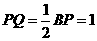 ∴PF=PQ①,
∴PF=PQ①,
∵A1E⊥平面BEP, 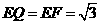 ∴A1E=A1Q,
∴A1E=A1Q,
∴△A1FP≌△A1QP从而∠A1PF=∠A1PQ②,
由①②及MP为公共边知△FMP≌△QMP,
∴∠QMP=∠FMP=90o,且MF=MQ,
从而∠FMQ为二面角B-A1P-F的平面角.
在Rt△A1QP中,A1Q=A1F=2,PQ=1,又∴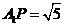 . ∵ MQ⊥A1P∴
. ∵ MQ⊥A1P∴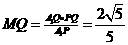 ∴
∴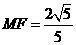 在△FCQ中,FC=1,QC=2,
∠C=600,由余弦定理得
在△FCQ中,FC=1,QC=2,
∠C=600,由余弦定理得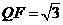
在△FMQ中,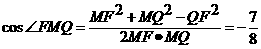
∴二面角B-A1P-F的大小为
[解后反思]在立体几何学习中,我们要多培养空间想象能力, 对于图形的翻折问题,关健是利用翻折前后的不变量,二面角的平面角的适当选取是立体几何的核心考点之一.是高考数学必考的知识点之一.作,证,解,是我们求二面角的三步骤.作:作出所要求的二面角,证:证明这是我们所求二面角,并将这个二面角进行平面化,置于一个三角形中,最好是直角三角形,利用我们解三角形的知识求二面角的平面角.向量的运用也为我们拓宽了解决立体几何问题的角度,不过在向量运用过程中,要首先要建系,建系要建得合理,最好依托题目的图形,坐标才会容易求得.
(11)在△ABC中,已知BC=12,A=60°,B=45°,则AC= ▲
(12)设变量x、y满足约束条件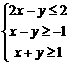 ,则
,则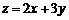 的最大值为 ▲
的最大值为 ▲
(13)今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有 ▲ 种不同的方法(用数字作答)。
(14)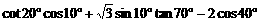 = ▲
= ▲
(15)对正整数n,设曲线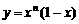 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为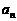 ,则数列
,则数列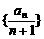 的前n项和的公式是 ▲
的前n项和的公式是 ▲
(16)不等式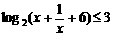 的解集为 ▲
的解集为 ▲
(1)已知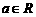 ,函数
,函数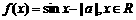 为奇函数,则a=
为奇函数,则a=
(A)0 (B)1 (C)-1 (D)±1
(2)圆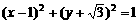 的切线方程中有一个是
的切线方程中有一个是
(A)x-y=0 (B)x+y=0 (C)x=0 (D)y=0
(3)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为
(A)1 (B)2 (C)3 (D)4
(4)为了得到函数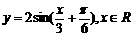 的图像,只需把函数
的图像,只需把函数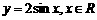 的图像上所有的点
的图像上所有的点
(A)向左平移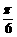 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的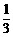 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移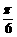 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的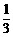 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移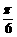 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移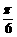 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(5)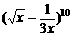 的展开式中含x的正整数指数幂的项数是
的展开式中含x的正整数指数幂的项数是
(A)0 (B)2 (C)4 (D)6
(6)已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足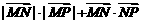 =0,则动点P(x,y)的轨迹方程为
=0,则动点P(x,y)的轨迹方程为
(A)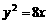 (B)
(B)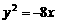 (C)
(C)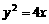 (D)
(D)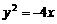
(7)若A、B、C为三个集合,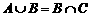 ,则一定有
,则一定有
(A)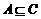 (B)
(B)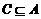 (C)
(C)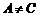 (D)
(D)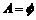
(8)设a、b、c是互不相等的正数,则下列等式中不恒成立的是
(A)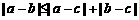 (B)
(B)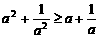
(C)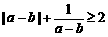 (D)
(D)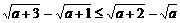
|
|
|
|
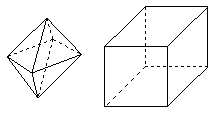 (9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
(9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
|
(C)3个 (D)无穷多个
 (10)右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是
(10)右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是
(A)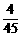 (B)
(B)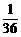
(C)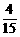 (D)
(D)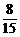
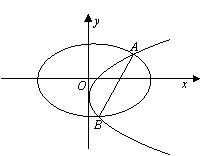
21. (本小题满分14分)已知椭圆C1: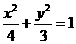 ,抛物线C2:
,抛物线C2: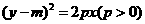 ,
,
且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅰ)当AB⊥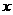 轴时,求
轴时,求 、
、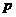 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在 、
、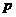 的值,使抛物线C2的焦点恰在直线AB上?若存在,
的值,使抛物线C2的焦点恰在直线AB上?若存在,
求出符合条件的 、
、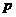 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为:
x =1,从而点A的坐标为(1,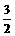 )或(1,-
)或(1,-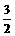 ). 因为点A在抛物线上.
). 因为点A在抛物线上.
所以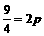 ,即
,即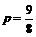 .此时C2的焦点坐标为(
.此时C2的焦点坐标为(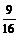 ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(II)解法一: 假设存在 、
、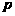 的值使
的值使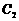 的焦点恰在直线AB上,由(I)知直线AB
的焦点恰在直线AB上,由(I)知直线AB
的斜率存在,故可设直线AB的方程为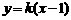 .
.
 由
由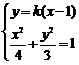 消去
消去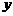 得
得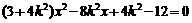 ………………①
………………①
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程①的两根,x1+x2=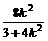 .
.
由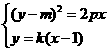
消去y得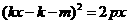 .
………………②
.
………………②
因为C2的焦点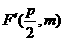 在直线
在直线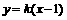 上,
上,
所以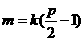 ,即
,即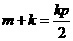 .代入②有
.代入②有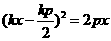 .
.
即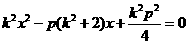 .
…………………③
.
…………………③
由于x1,x2也是方程③的两根,所以x1+x2=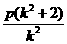 .
.
从而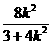 =
=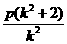 . 解得
. 解得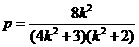 ……………………④
……………………④
又AB过C1、、\、、C2的焦点,所以
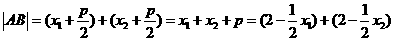 ,
,
则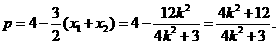 …………………………………⑤
…………………………………⑤
由④、⑤式得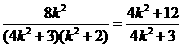 ,即
,即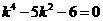 .
.
解得 于是
于是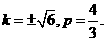
因为C2的焦点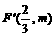 在直线
在直线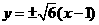 上,所以
上,所以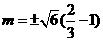 .
.

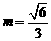 或
或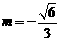 .
.
由上知,满足条件的 、
、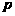 存在,且
存在,且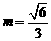 或
或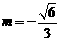 ,
,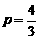 .
.
解法二: 设A、B的坐标分别为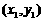 ,
,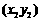 .
.
因为AB既过C1的右焦点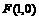 ,又过C2的焦点
,又过C2的焦点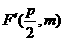 ,
,
所以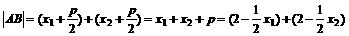 .
.
即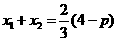 .
……①
.
……①
由(Ⅰ)知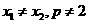 ,于是直线AB的斜率
,于是直线AB的斜率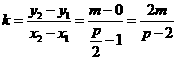 , ……②
, ……②
且直线AB的方程是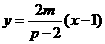 ,
,
所以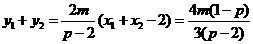 . ……③
. ……③
又因为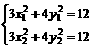 ,所以
,所以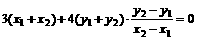 . ……④
. ……④
将①、②、③代入④得 . ……………⑤
. ……………⑤
因为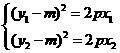 ,所以
,所以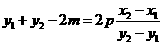 . …………⑥
. …………⑥
将②、③代入⑥得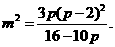 ……………⑦
……………⑦
由⑤、⑦得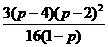
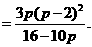 即
即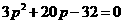
解得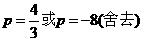 .将
.将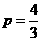 代入⑤得
代入⑤得

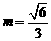 或
或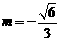 .
.
由上知,满足条件的 、
、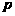 存在,且
存在,且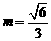 或
或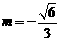 ,
,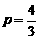
20. (本小题满分14分)对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为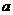 (1≤a≤3).设用
(1≤a≤3).设用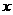 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是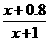 (
(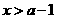 ),用
),用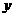 质量的水第二次清洗后的清洁度是
质量的水第二次清洗后的清洁度是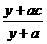 ,其中
,其中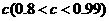 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(Ⅰ)分别求出方案甲以及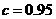 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当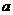 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论
为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论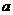 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
解:(Ⅰ)设方案甲与方案乙的用水量分别为x与z,由题设有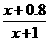 =0.99,解得x=19.
=0.99,解得x=19.
由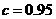 得方案乙初次用水量为3, 第二次用水量y满足方程:
得方案乙初次用水量为3, 第二次用水量y满足方程:
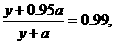 解得y=4
解得y=4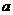 ,故z=4
,故z=4 +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4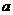 +3.
+3.
因为当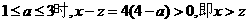 ,故方案乙的用水量较少.
,故方案乙的用水量较少.
(II)设初次与第二次清洗的用水量分别为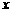 与
与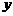 ,类似(I)得
,类似(I)得
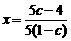 ,
,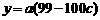 (*)
(*)
于是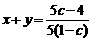 +
+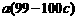
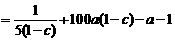
当 为定值时,
为定值时,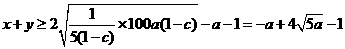 ,
,
当且仅当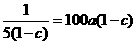 时等号成立.此时
时等号成立.此时

将 代入(*)式得
代入(*)式得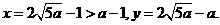
故 时总用水量最少, 此时第一次与第二次用水量分别为
时总用水量最少, 此时第一次与第二次用水量分别为
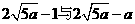 , 最少总用水量是
, 最少总用水量是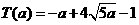 .
.
当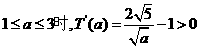 ,故T(
,故T(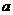 )是增函数(也可以用二次函数的单调性判断).这说明,随着
)是增函数(也可以用二次函数的单调性判断).这说明,随着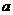 的值的最少总用水量, 最少总用水量最少总用水量.
的值的最少总用水量, 最少总用水量最少总用水量.
19. (本小题满分14分)已知函数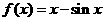 ,
,
数列{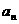 }满足:
}满足: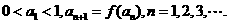
证明: (I).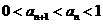 ;
;
(II).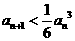 .
.
证明: (I).先用数学归纳法证明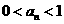 ,n=1,2,3,…
,n=1,2,3,…
(i).当n=1时,由已知显然结论成立.
(ii).假设当n=k时结论成立,即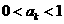 .因为0<x<1时
.因为0<x<1时
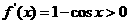 ,所以f(x)在(0,1)上是增函数. 又f(x)在[0,1]上连续,
,所以f(x)在(0,1)上是增函数. 又f(x)在[0,1]上连续,
从而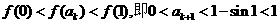 .故n=k+1时,结论成立.
.故n=k+1时,结论成立.
由(i)、(ii)可知,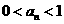 对一切正整数都成立.
对一切正整数都成立.
又因为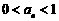 时,
时,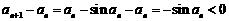 ,
,
所以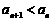 ,综上所述
,综上所述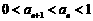 .
.
(II).设函数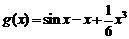 ,
,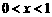 .由(I)知,当
.由(I)知,当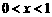 时,
时,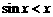 ,
,
从而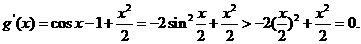
所以g (x)在(0,1)上是增函数. 又g (x)在[0,1]上连续,且g (0)=0,
所以当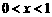 时,g (x)>0成立.于是
时,g (x)>0成立.于是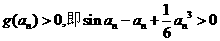 .
.
故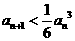 .
.
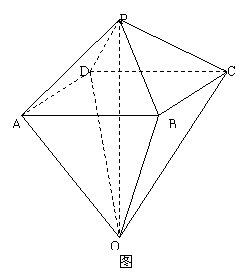
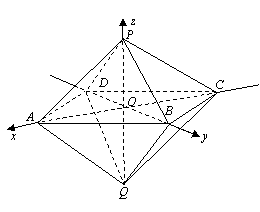
18. (本小题满分14分)如图4,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1
和2,AB=4. (Ⅰ)证明PQ⊥平面ABCD; (Ⅱ)求异面直线AQ与PB所成的角;
(Ⅲ)求点P到平面QAD的距离.
解法一: (Ⅰ).连结AC、BD,设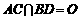 .由P-ABCD与Q-ABCD
.由P-ABCD与Q-ABCD
都是正四棱锥,所以PO⊥平面ABCD,QO⊥平面ABCD.
从而P、O、Q三点在一条直线上,所以PQ⊥平面ABCD.
(II)由题设知,ABCD是正方形,所以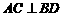 .由(I),
.由(I),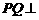 平面
平面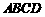 ,故可以分别以直线CA、DB、QP为
,故可以分别以直线CA、DB、QP为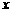 轴,
轴,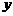 轴,
轴,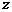 轴建立空间直角坐标系(如上图),由题设条件,相关各点的坐标分别是
轴建立空间直角坐标系(如上图),由题设条件,相关各点的坐标分别是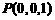 ,
,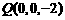 ,
,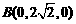
所以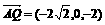 ,
,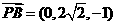 ,于是
,于是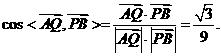
从而异面直线AQ与PB所成的角是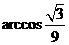 .
.
(Ⅲ).由(Ⅱ),点D的坐标是(0,-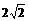 ,0),
,0),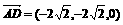 ,
,
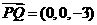 ,设
,设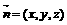 是平面QAD的一个法向量,
是平面QAD的一个法向量,
由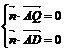 得
得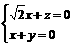 .
.
取x=1,得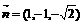 . 所以点P到平面QAD的距离
. 所以点P到平面QAD的距离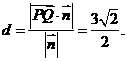 .
.
解法二: (Ⅰ).取AD的中点M,连结PM,QM.因为P-ABCD与Q-ABCD
都是正四棱锥,所以AD⊥PM,AD⊥QM. 从而AD⊥平面PQM.
又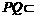 平面PQM,所以PQ⊥AD.同理PQ⊥AB,所以PQ⊥平面ABCD.
平面PQM,所以PQ⊥AD.同理PQ⊥AB,所以PQ⊥平面ABCD.
(Ⅱ).连结AC、BD设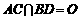 ,由PQ⊥平面ABCD及正四棱锥的性质可知O在
,由PQ⊥平面ABCD及正四棱锥的性质可知O在
PQ上,从而P、A、Q、C四点共面.
取OC的中点N,连结PN.
 因为
因为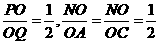 ,所以
,所以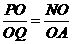 ,
,
从而AQ∥PN.∠BPN(或其补角)是异面直线AQ
与PB所成的角.连接BN,
因为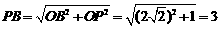 .
.
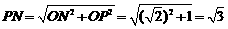
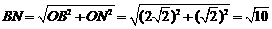
所以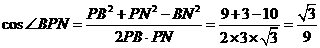 .
.
从而异面直线AQ与PB所成的角是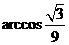 .
.
(Ⅲ).由(Ⅰ)知,AD⊥平面PQM,所以平面PQM⊥平面QAD. 过P作PH⊥QM
于H,则PH⊥平面QAD,所以PH的长为点P到平面QAD的距离.
连结OM,则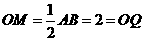 .所以
.所以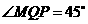 ,
,
又PQ=PO+QO=3,于是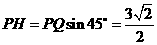 .
.
即点P到平面QAD的距离是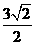 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com