
题目列表(包括答案和解析)
(四)排列、组合的混合问题
排列、组合的混合问题,主要指既与组合有关,又与排列有关的应用问题.如分配问题.
例6 六本不同的书,按下列条件,各有多少种不同的分法?
(1) 分为三堆,每堆2本;
(2) 分为三堆,一堆1本,一堆2本,一堆3本;
(3) 分给甲、乙、丙三人,每人2本;
(4) 分给甲、乙、丙三人,一人得1本,一人拿2本,一人得3本;
(5) 分给甲、乙、丙三人,每人至少得1本.
评析 本例属分配问题,解这类问题的基本思路是先分组,再分配,即先组合、后排列.同时注意在分组时,若出现平均分组(即两组元素个数相同)的情况,则要除以组数(即平均分组的数目)的阶乘.
例6 (1)分别从4所学校选拔6名报告员,每校至少1人,有多少种不同的选法?
(2) 将6名报告员分配到4所学校去做报告,每校至少1人,有多少种不同的分配方法?
评析 两小题看以类似,但第(1)小题的选取元素为学校;第(2)小题的选取元素为报告员,解题时要注意区分分组时,组合的对象--即元素是什么.
(三)排列应用题
例2 4位学生与2位教师并坐合影留念.(1)教师必须坐在中间;(2)教师不能坐在两端,但要坐在一起;(3)教师不能坐在两端,且不能相邻.各有多少种不同的坐法?(1)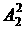 ;(2)
;(2)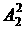
 ;(3)144
;(3)144
评析 (1) “在与不在”、“邻与不邻”是带限制条件的排列应用题的两种重要题型,处理这类问题的基本思路,有“直接”、“间接”之分.
(2) 对“在与不在”问题,优先考虑受限制的特殊元素或特殊位置的思想方法,是解题的基本策略;而处理“邻与不邻”问题,使用捆绑和插空法是十分有效的.
(3) 关于“元素和问题”的认识,是排列、组合概念中的一个重要问题,解题总是从元素或位置出发,要注意即使在同一问题中,把什么看作元素(或位置)并不是一成不变的.
例3 用0,1,2,3,4,5 六个数字,可以组成多少个没有重复数字的:(1)首数是奇数的五位偶数?(2) 五位奇数?(3)五位偶数?
(二)加法原理与乘法原理
这是两个基本原理,它们不仅是推导排列数公式、组合数公式的基础,而且可以直接运用它们去解决某些问题.两个原理的区别是前者与分类有关,与元素的顺序有关;后者与分步有关,与元素的顺序无关;.
例1 (1)有红、黄、白色旗子各n面(n>3),取其中一面、二面、三面组成纵列信号,可以有多少不同的信号?
(2) 有1元、5元、10元的钞票各一张,取其中一张或几张,能组成多少种不同的币值?
(1) 解 因为纵列信号有上、下顺序关系,所以是一个排列问题,信号分一面、二面、三面三种情况(三类),各类之间是互斥的,所以用加法原理:①升一面旗,共有3种信号;②升二面旗,要分两步,连续完成每一步,信号方告完成,而每步又是独立的事件,故用乘法原理,因同色旗子可重复使用,故共有3×3种信号;③升三面旗,有3×3×3种信号.所以共有39种信号.
(2) 解法 计算币值与顺序无关,所以是一个组合问题,有取一张、二张、三张、四张四种情况,它们彼此是互斥的,用加法原理.因此,不同币值有
 =15(种)
=15(种)
评析 (1) 排列、组合的区别在于顺序性,前者“有序”而后者“无序”;加法原理与乘法原理的区别在于联斥性,前者“斥”--互斥独立事件,后者“联”--相依事件.因而有“顺序”决“问题”,“联斥”定“原理”的说法.
(2)加、乘原理是排列、组合问题的理论依据,在分析问题和指导解题中起着关键作用,运用加法原理的关键在于恰当地分类(分情况),要使所分类别既不遗漏,也不重复;运用乘法原理的关键在于分步,要正确设计分步的程序,使每步之间既互相联系,又彼此独立.
(一)本来的主要内容结构
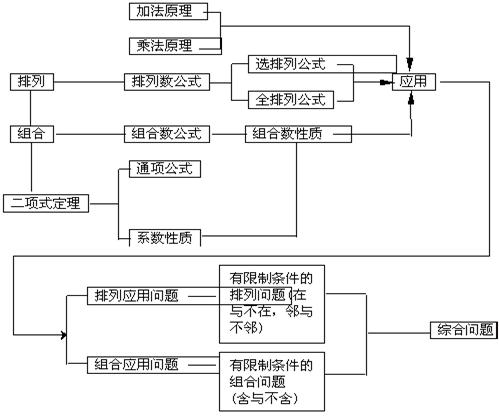
1. 掌握加法原理及乘法原理,并能运用这两个原理分析和解决一些简单的问题. 2. 理解排列、组合的意义,掌握排列数、组合数的计算公式和组合数的性质,并能用它们解决一些简单的问题. 3. 掌握二项式定理和二项式系数的性质,并能用它们计算和论证一些简单问题.
17、 如图,
如图, 是底面边长为
是底面边长为 的正三棱锥,
的正三棱锥, 、
、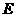 、
、 分别为棱
分别为棱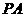 、
、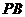 、
、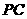 上的点,截面
上的点,截面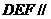 底面
底面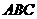 ,且棱台
,且棱台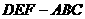 与棱锥
与棱锥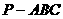 的棱长和相等。(棱长和是指多面体中所有棱的长度之和)
的棱长和相等。(棱长和是指多面体中所有棱的长度之和)
(1)证明: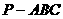 为正四面体;
为正四面体;
(2)若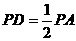 ,求二面角
,求二面角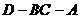 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)
(3)设棱台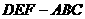 的体积为
的体积为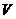 ,是否存在体积为
,是否存在体积为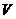 且各棱长均相等的直平行六面体,使得它与棱台
且各棱长均相等的直平行六面体,使得它与棱台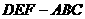 有相同的棱长和?若存在,请具体构造一个直平行六面体,并给出证明;若不存在,请说明理由。
有相同的棱长和?若存在,请具体构造一个直平行六面体,并给出证明;若不存在,请说明理由。
16、如图,将边长为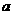 的正方形剪去图中的阴影部分,沿图中所画虚线折成一个正三棱锥。这个正三棱锥侧棱与底面所成角的余弦值是
的正方形剪去图中的阴影部分,沿图中所画虚线折成一个正三棱锥。这个正三棱锥侧棱与底面所成角的余弦值是
15、在 的二面角内,放一个半径为
的二面角内,放一个半径为 的球切两半平面于
的球切两半平面于 、
、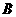 两点,那么这两个切点在球面上最短距离是
两点,那么这两个切点在球面上最短距离是
14、 已知球的表面积为
已知球的表面积为 ,有两个平行截面的面积分别为
,有两个平行截面的面积分别为 和
和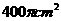 ,则这两个平行截面间的距离是
,则这两个平行截面间的距离是
13、正四面体的侧面与底面所成二面角的余弦值是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com