
题目列表(包括答案和解析)
1.若函数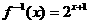 ,则
,则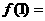 ( )
( )
A.4 B.-4 C.1 D.-1
(17)[解]∵
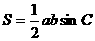 ∴
∴ 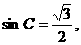 ……(4分)
……(4分)
于是∠C=60°,或∠C=120°. ……(6分)
又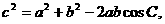
当 ∠C=60°时, ……(9分)
……(9分)
当 ∠C=120°时,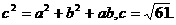 ……(12分)
……(12分)
(18) [解法一]由已知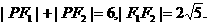 ……(4分)
……(4分)
根据直角的不同位置,分两种情况:
若∠PF2F1为直角,则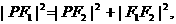
即 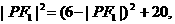
得 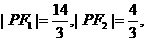 故
故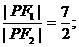 ……(9分)
……(9分)
若∠F1PF2为直角,则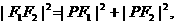
即 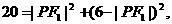
得 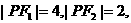 故
故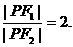 ……(12分)
……(12分)
[解法二] 由椭圆的对称性不妨设P(x,y) (x>0,y>0),
则由已知可得 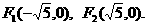 ……(4分)
……(4分)
根据直角的不同位置,分两种情况:
若∠PF2F1为直角,则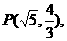
于是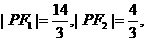 故
故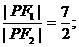 ……(9分)
……(9分)
若∠F1PF2为直角,则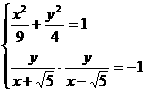 ,
,
解得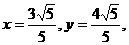 即
即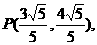
于是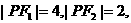 故
故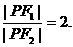 ……(12分)
……(12分)
(说明:两种情况,缺少一种扣3分)
(19)(1)[证明]如图,以O为原点建立空间直角坐标系。
设AE=BF=x,则
A’(a,0,a)、F(a-x,a,0)、C’(0,a,a)、E(a,x,0)
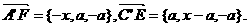 ……(4分)
……(4分)
∵ 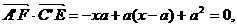
∴ A’F⊥C’E.
(2)[解]记BF=x,BE=y,则 x+y=a,
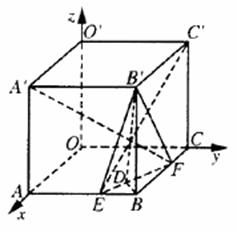
三棱锥B’-BEF的体积
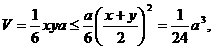
当且仅当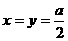 时,等号成立。
时,等号成立。
因此,三棱锥B’-BEF的体积取得最大值时,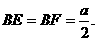 ……(10分)
……(10分)
过B作BD⊥EF交EF于D,连B’D,可知B’D⊥EF.
∴ ∠B’DB是二面角B’-EF-B的平面角。
在直角三角形BEF中,直角边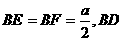 是斜边上的高,
是斜边上的高,
∴ 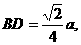
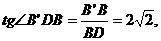
故二面角B’-EF-B的大小为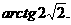 ……(14分)
……(14分)
(20)[解] (1)∵ z是方程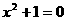 的根,
的根,
∴ z1=i 或 z2=-i. ……(2分)
不论 z1=i 或 z2=-i,
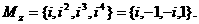 ……(8分)
……(8分)
于是 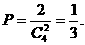 ……(10分)
……(10分)
(2)取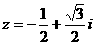 ,则
,则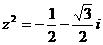 及
及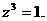
于是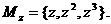
或取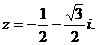 (说明:只需写出一个正确答案。)
(说明:只需写出一个正确答案。)
(21)[解](1)f(0)=1表示没有用水洗时,蔬菜上的农药量将保持原样。 ……(2分)
(2)函数f(x)应该满足的条件和具有的性质是:
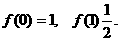
在[0,+∞]上f(x)单调递减,且0<f(x)≤1. ……(8分)
(3)设仅清洗一次,残留的农药量为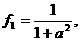
清洗两次后,残留的农药量为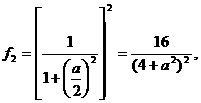 ……(12分)
……(12分)
则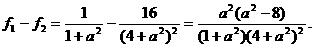
于是,当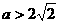 时,f1>f2;
时,f1>f2;
当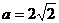 时,f1=f2;
时,f1=f2;
当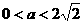 时,f1<f2;
时,f1<f2;
当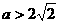 时,清洗两次后残留的农药量较少;
时,清洗两次后残留的农药量较少;
当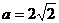 时,两种清洗方法具有相同的效果;
时,两种清洗方法具有相同的效果;
当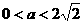 时,一次清洗残留的农药量较少.
……(16分)
时,一次清洗残留的农药量较少.
……(16分)
(22)[解](1)∵ f(x)的定义域D=(-∞,-1)∪(-1,+∞),∴ 数列{xn}只有三项:
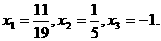 ……(3分)
……(3分)
(2)∵ 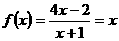 ,即
,即 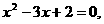
∴ x=1,或x=2.
即当x0=1或2时,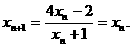
故当x0=1时,xn=1; 当x0=2时,xn=2 (n∈N). ……(9分)
(3)(证法一)设xn<0 (n∈N).
由
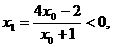 得
得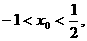
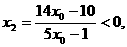 得
得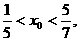
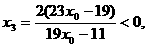 得
得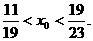
∵ 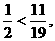 ∴ 同时使x1、x2、x3为负数的x0不存在。
∴ 同时使x1、x2、x3为负数的x0不存在。
故所求的x0不存在。 ……(18分)
(13)C (14)A (15)D (16)D
(1)3. (2) 153 (3)x2-4y2=1. (4)1
(5)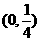 (6)(0,7) (7)7 (8)15
(6)(0,7) (7)7 (8)15
(9)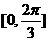 (10)A3
(10)A3
(11)设圆方程: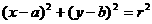 ①,
①,
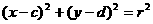 ②
②
(a≠c或b≠d),则由①-②,得两圆的对称轴方程。
(12)
3.第17题至第22题中右端所注的分数,表示考生正确做到这一步应得的该题的累加分数,给分或扣分均以1分为单位。
解答
2.评阅试卷,就坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响决定后面的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
(17)(本题满分12分)
已知a、b、c是△ABC中∠A、∠B、∠C的对边,S是△ABC的面积。若a=4,b=5,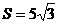 ,求c的长度.
,求c的长度.
[解]
(18)(本题满分12分)
设F1、F2为椭圆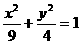 的两个焦点,P为椭圆上的一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求
的两个焦点,P为椭圆上的一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求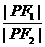 的值.
的值.
(解)
(19)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
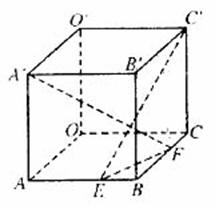
在棱长为a的正方体OABC-O’A’B’C’中,E、F分别是棱AB、BC上的动点,且AE=BF.
(1)求证:A’F⊥C’E;
(2)当三棱锥B’-BEF的体积取得最大值时,求二面角B’-EF-B的大小。(结果用反三角函数表示)
(1)[证明]
(2)[解]
(20)(本题满分14分)本题共有2个小题,第1小题满分10分,第2小题满分4分.
对任意一人非零复数z,定义集合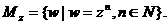
(1)设z是方程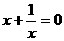 的一个根.试用列举法表示集合Mz,若在Mz中任取两个数,求其和为零的概率P;
的一个根.试用列举法表示集合Mz,若在Mz中任取两个数,求其和为零的概率P;
(2)若集合Mz中只有3个元素,试写出满足条件的一个z值,并说明理由.
[解] (1)
(2)
(21)(本题满分16分)本题共有3个小题,第1小题满分2分,第2小题满分6分,第3小题满分8分.
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量的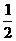 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上。设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上。设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).
(1)试规定f(0)的值,并解释其实际意义;
(2)试根据假定写出函数f(x)应该满足的条件和具有的性质;
(3)设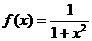 。现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由。
。现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由。
[解](1)
(2)
(3)
(22)(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
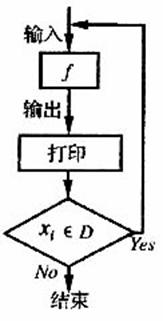
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
①输入数据x0∈D,经按列发生器,其工作原理如下:
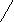 ②若x1∈D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=
f(x1),并依此规律继续下去,现定义
②若x1∈D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=
f(x1),并依此规律继续下去,现定义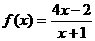 .
.
(1)若输入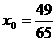 ,则由数列发生器产生数列{xn}。请写出数列{xn}的所有项:
,则由数列发生器产生数列{xn}。请写出数列{xn}的所有项:
(2)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据x0的值;
(3)若输入x0时,产生的无穷数列{xn}满足;对任意正整数n,均有xn > xn+1,求x0的取值范围。
[解](1)
(2)
(3)
数学试卷(类)答案要点及评分标准
说明:
1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分。
(13)a=3是直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行且不重合的
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既非充分也非必要条件
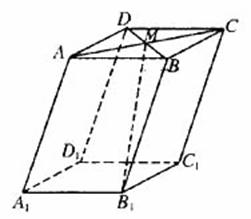
(14)如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点.若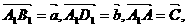 则下列向量中与
则下列向量中与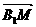 相等的向量是
相等的向量是
(A)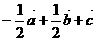 (B)
(B)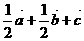
(C)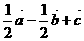 (D)
(D)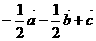
(15)已知a、b为两条不同的直线,α、β为两上不同的平面,且a⊥α、b⊥β,则下列命题中的假命题是
(A)若a∥b,则a∥β. (B)若α⊥β,则a⊥b.
(C)若a、b相交,则α、β相交. (D)若α、β相交,则a、b相交.
(16)用计算器验算函数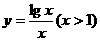 的若干个值,可以猜想下列命题中的真命题只能是
的若干个值,可以猜想下列命题中的真命题只能是
(A)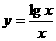 在(1,+∞)上是单调减函数
在(1,+∞)上是单调减函数
(B)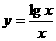 ,x∈(1,+∞)有最小值
,x∈(1,+∞)有最小值
(C)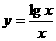 ,x∈(1,+∞)的值域为
,x∈(1,+∞)的值域为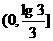
(D)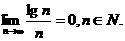
(1) 设函数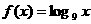 ,则满足
,则满足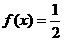 的x值为
.
的x值为
.
(2)设数列{a n}的首项a1=-7,则满足 则a1+a2+…+a17= .
则a1+a2+…+a17= .
(3)设P为双曲线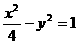 上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是
.
上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是
.
(4)设集合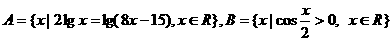 ,则A∩B的元素个数为
个.
,则A∩B的元素个数为
个.
(5)抛物线x2-4y-3=0的焦点坐标为 .
(6)设数列{a n}是公比q>0的等比数列,Sn是它的前n项和,若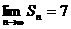 ,则此数列的首项a1的取值范围是
.
,则此数列的首项a1的取值范围是
.
(7)某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种。现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需准备不同的素菜品种 种.(结果用数值表示)
(8)在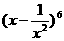 的二项展开式中,常数项为
.
的二项展开式中,常数项为
.
(9)设x=sin α,且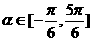 ,则arccosx的取值范围是
.
,则arccosx的取值范围是
.
(10)利用下列盈利表中的数据进行决策,应选择的方案是 .
|
自然状况 |
 方案 方案盈利(万元) 概率 |
A1 |
A2 |
A3 |
A4 |
|
S1 |
0.25 |
50 |
70 |
-20 |
98 |
|
S2 |
0.30 |
65 |
26 |
52 |
82 |
|
S3 |
0.45 |
26 |
16 |
78 |
-10 |
(11)已知两个圆: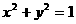 ①与
①与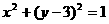 ②,则由①式减去②式可得上述两圆的对称轴方程。将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例。推广的命题为:
②,则由①式减去②式可得上述两圆的对称轴方程。将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例。推广的命题为:
.
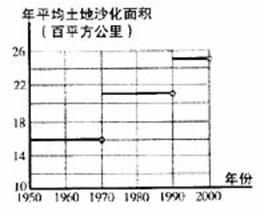
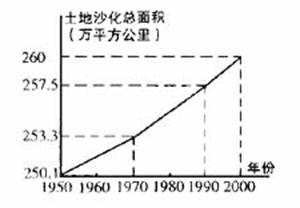
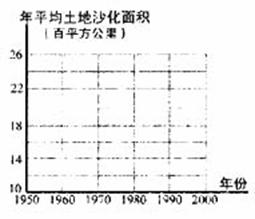
(12)据报道,我国目前已成为世界上受荒漠化危害最严重的国家之一,左下图表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况,由图中的相关信息,可将上述有关年代中,我国年平均土地沙化面积在右下图中图示为:
(17)本小题主要考查等差数列,一元二次方程与不等式的基本知识.考查综合运用数学基础知识的能力.满分12分.
解:依题意,有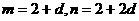 , ……2分
, ……2分
由方程有实根,得
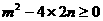 ,
,
即 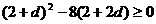 , ……6分
, ……6分
整理,得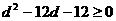 , ……8分
, ……8分
解得 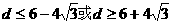 ,
,
∴ 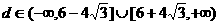 . ……12分
. ……12分
(18)本小题主要考查函数的基本性质,考查推理能力.满分12分.
解:函数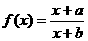 的定义域为
的定义域为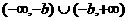 .
.
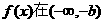 内是减函数
内是减函数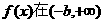 内也是减函数. ……4分
内也是减函数. ……4分
证明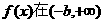 内是减函数.
内是减函数.
取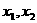
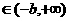 ,且
,且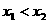 ,那么
,那么
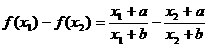
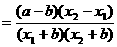 , ……6分
, ……6分
∵ 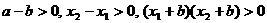 ,
,
∴ 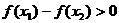 ,
,
即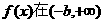 内是减函数. ……9分
内是减函数. ……9分
同理可证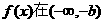 内是减函数. ……12分
内是减函数. ……12分
(19)本小题考查复数的基本概念和运算.满分12分.
解:(Ⅰ)由 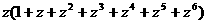
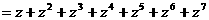
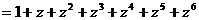 ,
,
得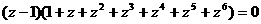 . ……4分
. ……4分
因为 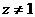 ,
,
所以 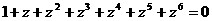 . ……6分
. ……6分
(Ⅱ)因为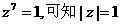 ,
,
所以 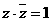 ,而
,而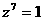 ,所以
,所以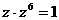 ,
,
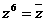 ,同理
,同理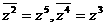 ,
,
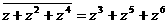 .
.
由(Ⅰ)知 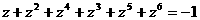 ,
,
即 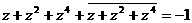 ,
,
所以
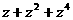 的实部为
的实部为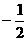 , ……8分
, ……8分
而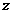 的辐角为
的辐角为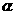 时,复数
时,复数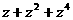 的实部为
的实部为
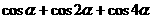 ,
,
所以 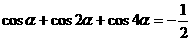 ……12分
……12分
(20)本小题考查运用直线与直线、直线与平面的基本性质证明线面关系的能力.满分12分.
(Ⅰ)证明:由已知,
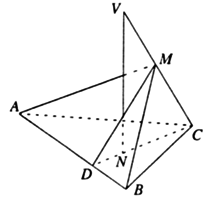
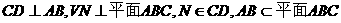 ,
,
∴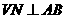 .
.
∴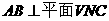 . ……2分
. ……2分
又V、M、N、D都在VNC所在平面内,
所以,DM与VN必相交,且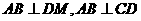 ,
,
∴∠MDC为二面角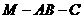 的平面角. ……4分
的平面角. ……4分
(Ⅱ)证明:由已知,∠MDC=∠CVN,
在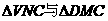 中,
中,
∠NCV=∠MCD,
又∵∠VNC=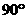 ,
,
∴∠DMC=∠VNC=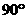 .
.
故有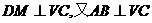 , ……6分
, ……6分
∴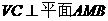 . ……8分
. ……8分
(Ⅲ)解:由(Ⅰ)、(Ⅱ),
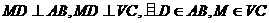 ,
,
∴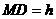 .
.
又∵∠ .
.
在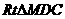 中,
中,
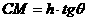 . ……10分
. ……10分
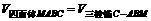
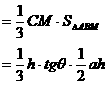
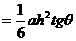 . ……12分
. ……12分
(21)本小题主要考查建立函数关系、运用不等式的性质和解法等数学知识解决实际问题的能力.满分12分.
解:(Ⅰ)由题意得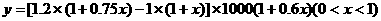 ,
,
……4分
整理得
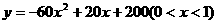 . ……6分
. ……6分
(Ⅱ)要保证本年度的利润比上年度有所增加,必须
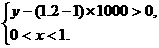
即 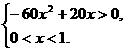 ……9分
……9分
解不等式得
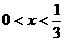 .
.
答:为保证本年度的年利润比上年度有所增加,投入成本增加的比例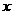 应满足
应满足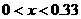 . ……12分
. ……12分
(22)本小题考查直线与抛物线的基本概念及位置关系,考查运用解析几何的方法解决数学问题的能力.满分14分.
解:(Ⅰ)直线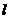 的方程为:
的方程为: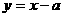 ,
,
将 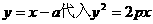 ,
,
得 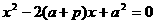 . ……2分
. ……2分
设直线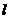 与抛物线两个不同交点的坐标为
与抛物线两个不同交点的坐标为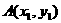 、
、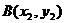 ,
,
则 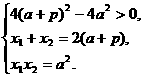 ……4分
……4分
又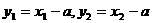 ,
,
∴ 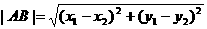
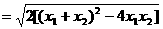
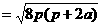 . ……6分
. ……6分
∵ 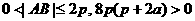 ,
,
∴ 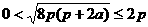 .
.
解得 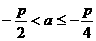 . ……8分
. ……8分
(Ⅱ)设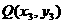 ,由中点坐标公式,得
,由中点坐标公式,得
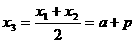 ,
,
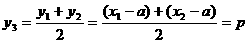 . ……10分
. ……10分
∴ 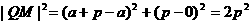 .
.
又 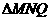 为等腰直角三角形,
为等腰直角三角形,
∴ 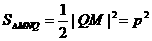 . ……14分
. ……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com