
题目列表(包括答案和解析)
(15)(本小题满分12分)
记函数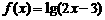 的定义域为集合M,函数
的定义域为集合M,函数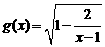 的定义域为集合
的定义域为集合 .求
.求
(Ⅰ)集合M, ;
;
(Ⅱ)集合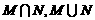 .
.
(16)(本小题满分14分)
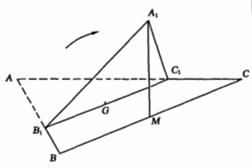 如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB,AC于
如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB,AC于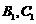 .将
.将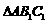 沿
沿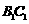 折起到
折起到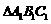 的位置,使点
的位置,使点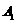 在平面
在平面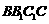 上的射影恰是线段BC的中点M.求
上的射影恰是线段BC的中点M.求
(Ⅰ)二面角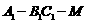 的大小;
的大小;
(Ⅱ)异面直线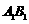 与
与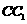 所成角的大小(用反三角函数表示).
所成角的大小(用反三角函数表示).
(17)(本小题满分14分)
已知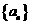 是等比数列,
是等比数列,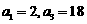 ;
;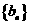 是等差数列,
是等差数列,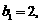
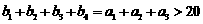
(Ⅰ)求数列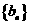 的通项公式;
的通项公式;
(Ⅱ)求数列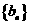 的前
的前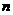 项和
项和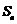 的公式;
的公式;
(Ⅲ)设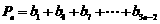 ,
,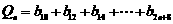
其中n=1,2,…,试比较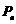 与
与 的大小,并证明你的结论
的大小,并证明你的结论
(18)(本小题满分14分)
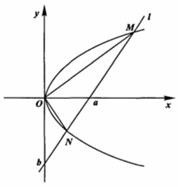 如图,O为坐标原点,直线
如图,O为坐标原点,直线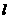 在
在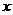 轴和
轴和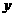 轴上的截距分别是
轴上的截距分别是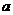 和
和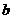 (
(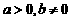 ),且交抛物线
),且交抛物线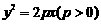 于
于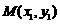 ,
,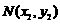 两点.
两点.
(Ⅰ)写出直线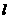 的截距式方程;
的截距式方程;
(Ⅱ)证明: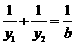
(Ⅲ)当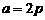 时,求
时,求 的大小
的大小
(19)(本小题满分13分)
经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量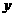 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度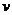 /(千米/小时)之间的函数关系为
/(千米/小时)之间的函数关系为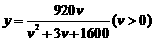
(Ⅰ)在该时段内,当汽车的平均速度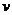 为多少时,车流量最大?最大车流量为多少? (精确到0.1千辆/小时)
为多少时,车流量最大?最大车流量为多少? (精确到0.1千辆/小时)
(Ⅱ)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
(20)(本小题满分13分)
现有一组互不相同且从小到大排列的数据: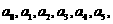 其中
其中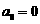 .为提取反映数据间差异程度的某种指标,今对其进行如下加工:记
.为提取反映数据间差异程度的某种指标,今对其进行如下加工:记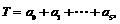 ,
,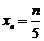 ,
,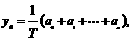 作函数
作函数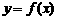 ,使其图象为逐点依次连接点
,使其图象为逐点依次连接点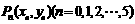 的折线.
的折线.
(Ⅰ)求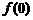 和
和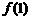 的值;
的值;
(Ⅱ)设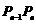 的斜率为
的斜率为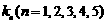 ,判断
,判断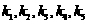 的大小关系;
的大小关系;
(Ⅲ)证明:当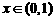 时,
时,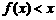 ;
;
(Ⅳ)求由函数y=x与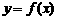 的图象所围成图形的面积(用
的图象所围成图形的面积(用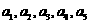 表示).
表示).
(9)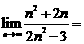 .
.
(10)已知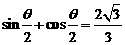 ,那么
,那么 的值为 ,
的值为 ,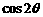 的值为 .
的值为 .
(11)若圆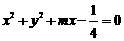 与直线
与直线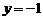 相切,且其圆心在
相切,且其圆心在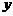 轴的左侧,则m的值为 .
轴的左侧,则m的值为 .
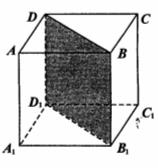 (12)如图,正方体
(12)如图,正方体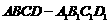 的棱长为
的棱长为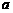 .将该正方体沿对角面
.将该正方体沿对角面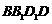 切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为 .
切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为 .
(13)从-1,0,1,2这四个数中选三个不同的数作为函数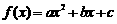 的系数,可组成不同的二次函数共有 个,其中不同的偶函数共有 个(用数字作答).
的系数,可组成不同的二次函数共有 个,其中不同的偶函数共有 个(用数字作答).
(14)若关于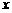 的不等式
的不等式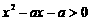 的解集为
的解集为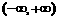 ,则实效
,则实效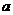 的取值范围是 ;若关于
的取值范围是 ;若关于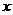 的不等式
的不等式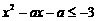 的解集不是空集,则实数
的解集不是空集,则实数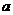 的取值范围是 .
的取值范围是 .
(1)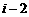 的共轭复数是
的共轭复数是
A.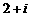 B.
B.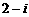 C.
C.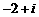 D.
D.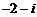
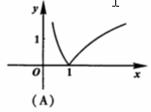
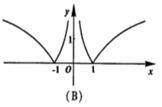
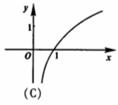
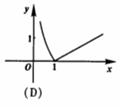
(2)函数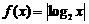 的图象是
的图象是
(3)有如下三个命题:
①分别在两个平面内的两条直线-定是异面直线;
②垂直于同一个平面的两条直线是平行直线;
③过平面。的一条斜线有一个平面与平面。垂直.
其中正确命题的个数为
A.0 B.1 C.2 D.3
(4)如果函数
 的最小正周期是
的最小正周期是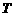 ,且当
,且当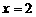 时取得最大值,那么
时取得最大值,那么
A.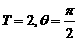 B.
B.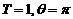 C.
C.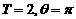 D.
D.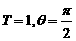
(5)设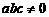 .“
.“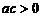 ”是“曲线
”是“曲线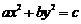 为椭圆”的
为椭圆”的
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
(6)已知双曲线的两个焦点为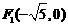 ,
,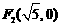 ,
,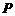 是此双曲线上的一点,且
是此双曲线上的一点,且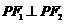 ,
,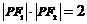 ,则该双曲线的方程是
,则该双曲线的方程是
A.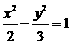 B.
B.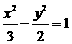 C.
C.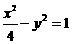 D.
D. 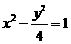
(7)在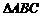 中,已知
中,已知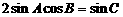 ,那么
,那么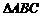 一定是
一定是
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.正三角形
(8)若不等式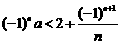 对于任意正整数n恒成立,则实数
对于任意正整数n恒成立,则实数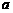 的取值范围是
的取值范围是
A.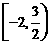 B.
B.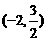 C.
C.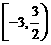 D.
D.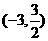
第Ⅱ卷
(15)(本小题满分12分)
 记函数
记函数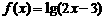 的定义域为集合M,函数
的定义域为集合M,函数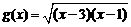 的定义域为集合
的定义域为集合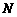 .求
.求
(Ⅰ)集合M,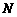 ;
;
(Ⅱ)集合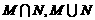 .
.
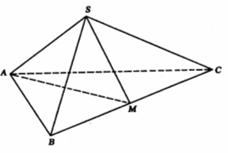
(16)(本小题满分14分)
如果正三棱锥S-ABC中,底面的边长为3,棱锥的侧面积等于底面积的2倍,M是BC的中点。求
(Ⅰ)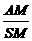 的值 (Ⅱ)二面角
的值 (Ⅱ)二面角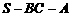 的大小;
的大小;
(Ⅲ)正三棱锥S-ABC的体积.
(17)(本小题满分14分)
已知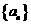 是等比数列,
是等比数列,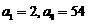 ;
;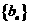 是等差数列,
是等差数列,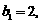
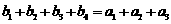
(Ⅰ)求数列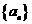 的通项公式及前
的通项公式及前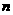 项和
项和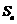 的公式;
的公式;
(Ⅱ)求数列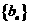 的通项公式;
的通项公式;
(Ⅲ)设 ,其中n=1,2,…,求
,其中n=1,2,…,求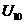 的值
的值
(18)(本小题满分14分)
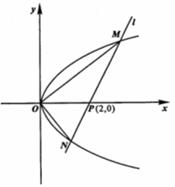 如图,O为坐标原点,过点
如图,O为坐标原点,过点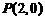 且斜率为
且斜率为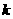 的直线
的直线 交抛物线
交抛物线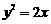 于
于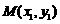 ,
,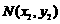 两点.
两点.
(Ⅰ)写出直线 的方程;
的方程;
(Ⅱ)求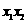 与
与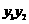 的值
的值
(Ⅲ)求证: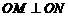
(19)(本小题满分13分)
经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量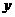 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度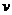 /(千米/小时)之间的函数关系为
/(千米/小时)之间的函数关系为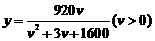
(Ⅰ)在该时段内,当汽车的平均速度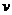 为多少时,车流量最大?最大车流量为多少? (精确到0.1千辆/小时)
为多少时,车流量最大?最大车流量为多少? (精确到0.1千辆/小时)
(Ⅱ)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
(20)(本小题满分13分)
现有一组互不相同且从小到大排列的数据: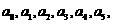 其中
其中 .为提取反映数据间差异程度的某种指标,今对其进行如下加工:记
.为提取反映数据间差异程度的某种指标,今对其进行如下加工:记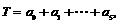 ,
,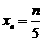 ,
,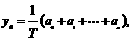 作函数
作函数 ,使其图象为逐点依次连接点
,使其图象为逐点依次连接点 的折线.
的折线.
(Ⅰ)求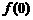 和
和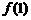 的值;
的值;
(Ⅱ)设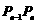 的斜率为
的斜率为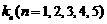 ,判断
,判断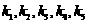 的大小关系;
的大小关系;
(Ⅲ)证明: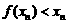
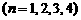 ;
;
(Ⅳ)求由函数y=x与 的图象所围成图形的面积(用
的图象所围成图形的面积(用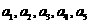 表示).
表示).
(9)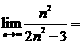 .
.
(10)椭圆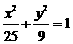 的离心率是
,准线方程是
。
的离心率是
,准线方程是
。
(11)已知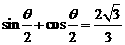 ,那么
,那么 的值为 ,
的值为 ,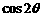 的值为 .
的值为 .
 (12)如图,正方体
(12)如图,正方体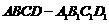 的棱长为
的棱长为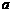 .将该正方体沿对角面
.将该正方体沿对角面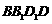 切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为 .
切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为 .
(13)从-1,0,1,2这四个数中选三个不同的数作为函数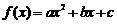 的系数,可组成不同的二次函数共有 个,其中不同的偶函数共有 个(用数字作答).
的系数,可组成不同的二次函数共有 个,其中不同的偶函数共有 个(用数字作答).
(14)若关于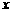 的不等式
的不等式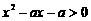 的解集为
的解集为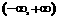 ,则实效
,则实效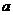 的取值范围是 ;
的取值范围是 ;
(1)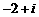 的共轭复数是
的共轭复数是
A.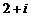 B.
B.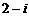 C.
C.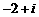 D.
D.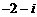
(2)函数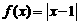 的图象是
的图象是
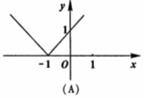
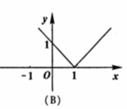
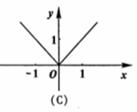
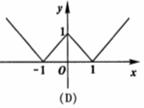
(3)下列命题中,正确的是:
A.经过不同的三点有且只有一个平面 B.分别在两个平面内的两条直线-定是异面直线 C.垂直于同一个平面的两条直线是平行直线 D.垂直于同一个平面的两个平面平行
(4)如果函数
 的最小正周期是
的最小正周期是 ,且当
,且当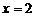 时取得最大值,那么
时取得最大值,那么
A.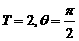 B.
B.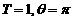 C.
C.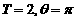 D.
D.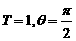
(5) “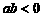 ”是“曲线
”是“曲线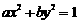 为双曲线”的
为双曲线”的
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
(6)直线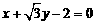 被圆
被圆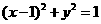 所截得的线段的长为
所截得的线段的长为
A.1 B.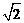 C.
C.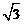 D. 2
D. 2
(7)在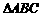 中,已知
中,已知 ,那么
,那么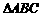 一定是
一定是
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.正三角形
(8)若不等式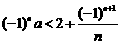 对于任意正整数n恒成立,则实数
对于任意正整数n恒成立,则实数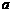 的取值范围是
的取值范围是
A.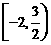 B.
B.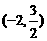 C.
C.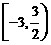 D.
D.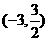
第Ⅱ卷
(17)(本小题满分12分)
解不等式: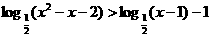 .
.
(18)(本小题满分12分)
已知函数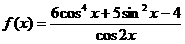 ,求f(x)的定义域,判断它的奇偶性,并求其值域.
,求f(x)的定义域,判断它的奇偶性,并求其值域.
 (19)(本小题满分12分)
(19)(本小题满分12分)
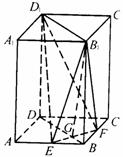
如图,正四棱柱ABCD-A1B1C1D1中,底面边长为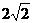 ,侧棱长为4.E,F分别为棱AB,BC的中点,
,侧棱长为4.E,F分别为棱AB,BC的中点,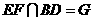 .
.
(Ⅰ)求证:平面B1EF⊥平面BDD1B1;
(Ⅱ)求点D1到平面B1EF的距离d;
(Ⅲ)求三棱锥B1-EFD1的体积V.
(20)(本小题满分12分)
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护需50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
(21)(本小题满分13分)
如图,在边长为l的等边△ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB,BC相切,…,圆On+1与圆On外切,且与AB,BC相切,如此无限继续下去.记圆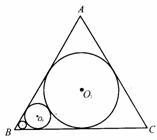 On的面积为an(n∈N).
On的面积为an(n∈N).
(Ⅰ)证明{an}是等比数列;
(Ⅱ)求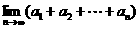 的值.
的值.
(22)(本小题满分13分)
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
(Ⅰ)求动圆圆心的轨迹M的方程;
(Ⅱ)设过点P,且斜率为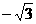 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.
(ⅰ)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ⅱ)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
普通高等学校春季招生考试
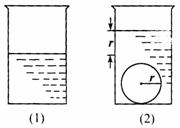 (13)如图,一个底面半径为R的圆柱形量杯中装有适量的
(13)如图,一个底面半径为R的圆柱形量杯中装有适量的
水.若放入一个半径为r的实心铁球,水面高度恰好升
高r,则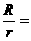 ____________.
____________.
(14)在某报《自测健康状况》的报道中,自测血压结果与相
应年龄的统计数据如下表,观察表中数据的特点,用适当的数填入表中空白(____)内.
|
年龄(岁) |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
|
收缩压(水银柱 毫米) |
110 |
115 |
120 |
125 |
130 |
135 |
(___) |
145 |
|
舒张压(水银柱 毫米) |
70 |
73 |
75 |
78 |
80 |
83 |
(___) |
88 |
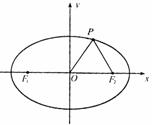 (15)如图,F1,F2分别为椭圆
(15)如图,F1,F2分别为椭圆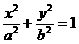 的左、右焦点,点P
的左、右焦点,点P
在椭圆上△POF2是面积为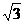 的正三角形,则b2的值是
的正三角形,则b2的值是
_________________.
(16)若存在常数p>0,使得函数f(x)满足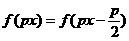 (x∈R),则f(x)的一个正周期为_____________.
(x∈R),则f(x)的一个正周期为_____________.
(1)若集合M={y | y=2-x},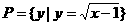 ,则
,则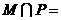

(2)若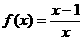 ,则方程f(4x)=x的根是
,则方程f(4x)=x的根是
(A)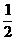 (B)
(B)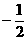 (C)
(D)-2
(C)
(D)-2
(3)设复数z1=-1+i,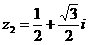 ,则
,则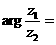
(A)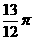 (B)
(B)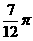 (C)
(C)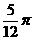 (D)
(D)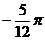
(4)函数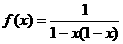 的最大值是
的最大值是
(A)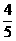 (B)
(B)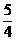 (C)
(C)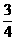 (D)
(D)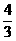
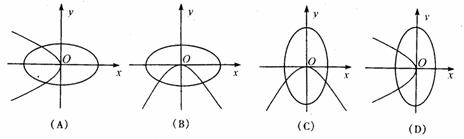
(5)在同一坐标系中,方程a2x2+b2y2=1与ax+by2=0(a>b>0)的曲线大致是
(6)若A,B,C是△ABC的三个内角,且A<B<C(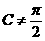 ),则下列结论中正确的是
),则下列结论中正确的是
(A)sinA<sinC (B)cosA<cosC
(C)tanA<tanC (D)cotA<cotC
(7)椭圆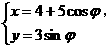 (j为参数)的焦点坐标为
(j为参数)的焦点坐标为
(A)(0,0),(0,-8) (B)(0,0),(-8,0)
 (C)(0,0),(0,8)
(D)(0,0),(8,0)
(C)(0,0),(0,8)
(D)(0,0),(8,0)
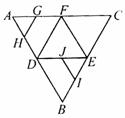
(8)如图,在正三角形ABC中,D,E,F分别为各边的中点, G,
H,I,J分别为AF,AD,BE,DE的中点.将△ABC沿DE,EF,
DF折成三棱锥以后,GH与IJ所成角的度数为
(A)90° (B)60° (C)45° (D)0°
(9)某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个节目插入原节目单中,那么不同插法的种数为
(A)42 (B)30 (C)20 (D)12
(10)已知直线ax+by+c=0(abc≠0)与圆x2+y2=1相切,则三条边长分别为| a |,| b |,| c |的三角形
(A)是锐角三角形 (B)是直角三角形
(C)是钝角三角形 (D)不存在
(11)若不等式| ax+2 | < 6的解集为(-1,2),则实数a等于
(A)8 (B)2 (C)-4 (D)-8
(12)在直角坐标系xOy中,已知△AOB三边所在直线的方程分别为x=0,y=0,2x+3y=30,则△AOB内部和边上整点(即横、纵坐标均为整数的点)的总数是
(A)95 (B)91
(C)88 (D)75
第Ⅱ卷(非选择题 共90分)
(六)二项式定理
内容:1 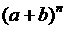 的展开式、项数、
的展开式、项数、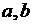 的指数。
的指数。
2 展开式中的通项公式
3 各项系数和的求法及各项二项式系数和的求法。
4 二项式系数最要的项,是第几项?(由n的奇偶性讨论)
5 注意展开式的逆用。
6 用二项式定理求近似值;证明整除问题。
例7 已知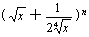 的展开式前三项中的x的系数成等差数列.
的展开式前三项中的x的系数成等差数列.
① 求展开式里所有的x的有理项;
② 求展开式中二项式系数最大的项.
评析 (1) 把握住二项展开式的通项公式,是掌握二项式定理的关键.除通项公式外,还应熟练掌握二项式的指数、项数、展开式的系数间的关系、性质.
(2) 应用通项公式求二项展开的特定项,如求某一项,含x某次幂的项,常数项,有理项,系数最大的项等,一般是应用通项公式根据题意列方程,在求得n或r后,再求所需的项(要注意n和r的数值范围及大小关系).
(3) 注意区分展开式“第r+1项的二项式系数”与“第r+1项的系数”.
例8 (’96 全国)某地现有耕地1000公顷.规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%,如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?

解 设耕地平均每年至少只能减少x公顷,又设该地区现有人口为P人,粮食单产为M顷.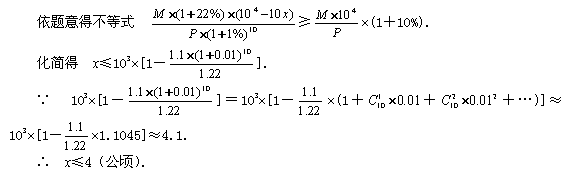
答:按规划该地区耕地每年至多只能减少4公顷.
评析 二项式定理的应用十分广泛,主要有以下四个方面:求展开式的特定项;近似计算;证明整除性和不等式;证明组合数等式或求和.本例的最后运用了二项展开式进行近似计算.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com