
题目列表(包括答案和解析)
1、等差数列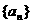 中,已知
中,已知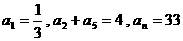 ,则
,则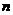 为( )
为( )
A、48 B、49 C、 D、51
12、(1)原式=1;(2)原式=1。
4、若lg2=a,lg3=b,则log512等于( )
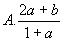
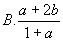
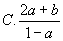
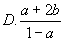
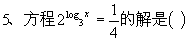
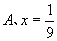
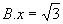
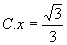
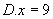
6、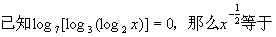 ( )
( )
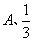
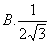
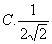
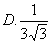
7、y=(0.2)-x+1的反函数是( )
A、y=log5x+1(x>0) B、y=log5x+1(x>0且x≠1)
C、y=log5(x+1)(x>-1) D、y=log5(x-1)(x>1)
8、已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
A、(0,1) B、(1,2) C、(0,2) D、[2,+∞)
9、若0<a<1,则log3(log3a)是( )
A、正数 B、负数 C、零 D、无意义
10、已知a=log32,那么log38-2log36用a表示是( )
A.a-2 B.5a-2 C.3a-(1+a)2 D.3a-a2-1
11、若log2[log0.5(log2x)]=0,则x=________。
12、计算
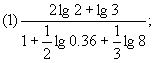
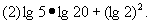
答案:
1-5 C A A C A
6-10 C D B D A
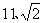
1、在b=log(a-2)(5-a)中,实数a的范围是( )
A、a>5或a<2 B、2<a<5 C、2<a<3或3<a<5 D、3<a<4
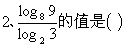
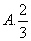 B、1
B、1
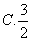 D、2
D、2
3、若logab=logba(a≠b),则ab=( )
A、1 B、2
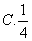 D、4
D、4
第一阶梯
[例1]将下列对数式化为指数式,指数式化为对数式:
(1)log216=4; 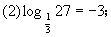 (3)54=625;
(3)54=625; 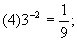
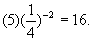
解:(1)24=16
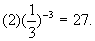
(3)∵54=625,∴log5625=4.
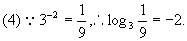
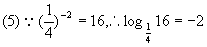
[例2]解下列各式中的x:
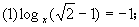
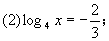
(3)2x=3;
(4)log3(x-1)=log9(x+5).
解: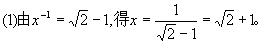
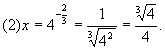
(3)x=log23.
(4)将方程变形为
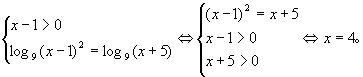
[例3]求下列函数的定义域:
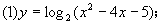
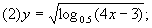
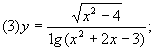
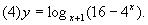
思路分析:
求定义域即求使解析式有意义的x的范围,真数大于0、底大于0且不等于1是对数运算有意义的前提条件。
解:(1)令x2-4x-5>0,得(x-5)(x+1)>0,故定义域为{x|x<-1,或x>5}
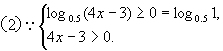
∴0<4x-3≤1。
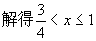
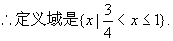
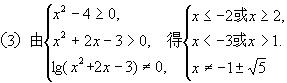
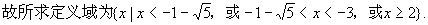

所以所求定义域为{x|-1<0,或0<x<2}.
第二阶梯
[例4]比较下列各组数中两个值的大小
(1)log23.4, log28.5;
(2)log0.31.8, log0.32.7;
(3)loga5.1, loga5.9(a>0,a≠1)。
思路分析:
题中各组数可分别看作对数函数y=log2x、y=log0.3x、y=logax的两函数值,可由对数函数的单调性确定。
解:(1)因为底数2>1,所以对数函数y=log2x在(0,+∞)上是增函数,于是log23.4<log28.5;
(2)因为底数为0.3,又0<0.3<1,所以对数函数y=log0.3x在(0,+∞)上是减函数,于是log0.31.8>
log0.32.7;
(3)当a>1时,函数y=logax在(0,+∞)上是增函数,所以loga5.1<loga5.9;
当0<a<1时,函数 y=logax在(0,+∞)上是减函数,所以loga5.1>loga5.9。
说明:本题是利用对数函数的单调性比较两对数的大小问题,对底数与1的大小关系未明确指定时,要分
情况对底数进行讨论来比较两个对数的大小,利用函数单调性比较对数的大小,是重要的基本方
法。
[例5]若a>0,a≠1,x>0,y>0,x>y,下列式子中正确的个数是( )
(1)logax·logay=loga(x+y);
(2)logax-logay=loga(x-y);
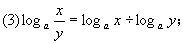
(4)logaxy=logax·logay;
A、0 B、1 C、2 D、3
思路分析:
对数的运算实质是把积、商、幂的对数运算分别转化为对数的加、减、乘的运算。在运算中要注意不能把
对数符号当作表示数的字母参与运算。如logax≠loga·x,logax是不可分开的一个整体。4个选项都把对
数符号当作字母参与运算,因此都是错误的。
答案:A
[例6]已知lg2=0.3010,lg3=0.4771,求 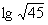 。
。
思路分析:解本题的关键是设法将 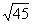 的常用对数分解为2,3的常用对数代入计算。
的常用对数分解为2,3的常用对数代入计算。
解: 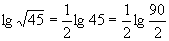
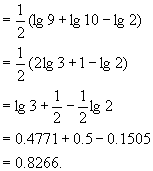
第三阶梯
[例7]若方程lg(ax)·lg(ax2)=4的所有解都大于1,求a的取值范围。
思路分析:由对数的性质,方程可变形为关于lgx的一元二次方程,化归为一元二次方程解的讨论问题。
解:原方程化为
(lgx+lga)(lga+2lgx)=4。
2lg2x+3lga·lgx+lg2a-4=0,
令t=lgx,则原方程等价于
2t2+3tlga+lg2a-4=0,(*)
若原方程的所有解都大于1,则方程(*)的所有解均大于0,则
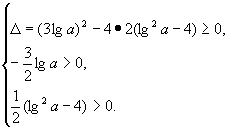
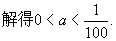
说明:换元要确保新变量与所替换的量取值范围的一致性。
[例8]将y=2x的图像( )
A、先向左平行移动1个单位
B、先向右平行移动1个单位
C、先向上平行移动1个单位
D、先向下平行移动1个单位
再作关于直线y=x对称的图像,可得函数y=log2(x+1)的图像。
思路分析:由于第二步的变换结果是已知的,故本题可逆向分析。
解法1:在同一坐标系内分别作为y=2x与y=log2(x+1)的图像,直接观察,即可得D。
解法2:与函数y=log2(x+1)的图像关于直线y=x以对称的曲线是它的反函数y=2x-1的图像,为了得到它,
只需将y=2x的图像向下平移1个单位。
解法3:
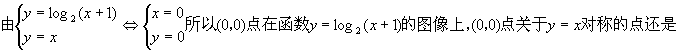
本身。函数y=2x的图像向左或向右或向上平行移动都不会过(0,0)点,因此排除A、B、C,即得D。
说明:本题从多角度分析问题、解决问题,注意培养思维的灵活性。
[例9]已知log189=a,18b=5,求log3645的值;(用含有a、b的式子表示)
思路分析:
当指数的取值范围扩展到有理数后,对数运算就是指数运算的逆运算(扩展之前开方运算是乘方运算的逆
运算)。因此,当一个题目中同时出现指数式和对数式时,一般要把问题转化,即统一到一种表达形式
上。
解:由18b=5,得b=log185,
又log189=a,
∴log189+log185=log3645=a+b,则
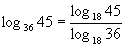
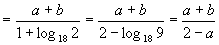
说明:在解题过程中,根据问题的需要指数式转化为对数式,或者对数式转化为指数式运算,这正是数
学转化思想的具体体现,转化思想是中学重要的教学思想,要注意学习、体会,逐步达到灵活应
用。
8、培养图形结合、化归等思想。
7、掌握比较对数大小的方法,培养应用意识;
6、掌握对数函数的图像的性质;
5、掌握对数函数的概念;
4、培养应用意识、化归意识。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com