
题目列表(包括答案和解析)
16、解:(1)设P(x0,y0)(x0>a,y0>0),又有点
A(-a,0),B(a,0).

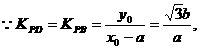 …………………………(7分)
…………………………(7分)
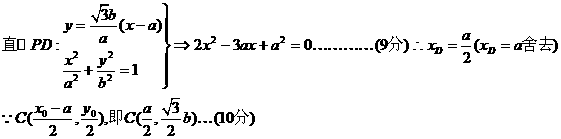
∴CD垂直于x轴.若CD过椭圆C1的右焦点,则
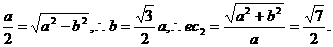
故可使CD过椭圆C1的右焦点,此时C2的离心率为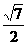 .…………(12分)
.…………(12分)
15、解:设初中x个班,高中y 个班,则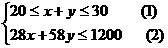 ……………(4分)
……………(4分)
设年利润为s,则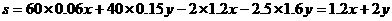 ……(6分)
……(6分)
作出(1)、(2)表示的平面区域,如图,易知当直线1.2x+2y=s过点A时,s有最大值.
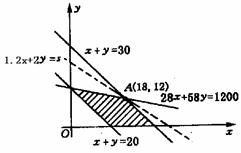 由
由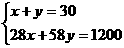 解得A(18,12).……(10分)
解得A(18,12).……(10分)
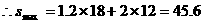 (万元).
(万元).
即学校可规划初中18个班,高中12个班,
可获最大年利润为45.6万元.……(12分)
14、(1)解:作出椭圆的左准线l,作MN⊥l交l于点N.
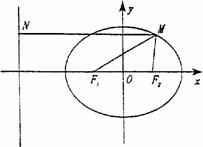 设
设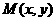 ,椭圆的离心率是e,椭圆的半焦距是c.
,椭圆的离心率是e,椭圆的半焦距是c.
根据椭圆的定义得: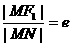 ,所以
,所以
 ,同理可得:
,同理可得:
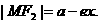 所以
所以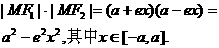
由||MF1|·||MF2|的最小值为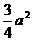 得:
得:
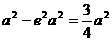 ,解得
,解得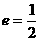 …………4分
…………4分
[注:若学生没有证明|MF1|=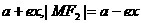
而直接使用此结论,则(Ⅰ)中扣去1分]
(Ⅱ)解:依题意得双曲线C2的离心率为2,
设C2的方程是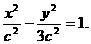 假设存在适合题意的常
假设存在适合题意的常
数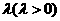 ,①先来考查特殊情形下的
,①先来考查特殊情形下的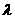 值:
值:
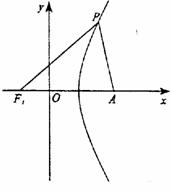
PA⊥x轴时,将x=2c代入双曲线方程,解得|y|=3c,
因为|AF1|=3c,所以△PAF1是等腰直角三角形,
∠PAF1=90°,∠PF1A=45°,此时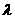 =2………7分
=2………7分
②以下证明当PA与x轴不垂直时,∠PAF1=2∠PF1A恒成立.
设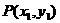 ,由于点P在第一象限内,所以直线PF1斜率存在,
,由于点P在第一象限内,所以直线PF1斜率存在,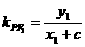 ;
;
因为PA与x轴不垂直,所以直线PA斜率也存在,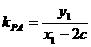 .
.
 因为
因为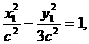 所以
所以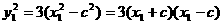 ,将其代入上式并化简得:
,将其代入上式并化简得:
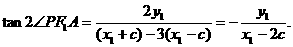 因为∠PAF1+∠PAx=180°,
因为∠PAF1+∠PAx=180°,
所以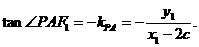 即tan2∠PF1A=tg∠PAF1.………………12分
即tan2∠PF1A=tg∠PAF1.………………12分
因为∠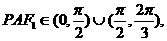 ∠
∠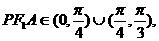 所以∠PAF1、
所以∠PAF1、
2∠PF1A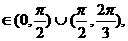 所以∠PAF1=2∠PF1A恒成立.
所以∠PAF1=2∠PF1A恒成立.
综合①、②得:存在常数 ,使得对位于双曲线C2在第一象限内的任意一点p,
,使得对位于双曲线C2在第一象限内的任意一点p,
∠PAF1=2∠PF1A恒成立.……………………14分
[注:②中如果学生认为∠PAF1、2∠PF1A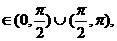 本题不扣分]
本题不扣分]
13、(I)由题意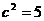 ,设
,设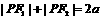 (
(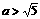 ),由余弦定理, 得
),由余弦定理, 得
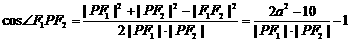 .
.
又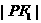 ·
·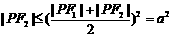 ,当且仅当
,当且仅当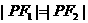 时,
时,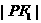 ·
·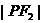 取最大值,
取最大值,
此时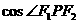 取最小值
取最小值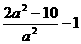 ,令
,令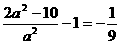 ,解得
,解得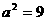 ,
,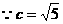 ,∴
,∴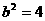 ,故所求
,故所求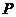 的轨迹方程为
的轨迹方程为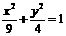 .
.
(II)设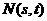 ,
,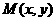 ,则由
,则由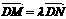 ,可得
,可得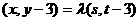 ,
,
故 ,∵
,∵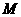 、
、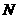 在动点
在动点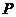 的轨迹上,故
的轨迹上,故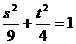 且
且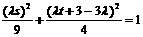 ,消去
,消去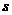 可得
可得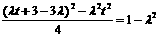 ,解得
,解得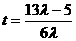 ,
,
又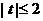 ,∴
,∴ ,解得
,解得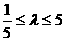 ,故实数
,故实数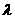 的取值范围是
的取值范围是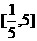 .
.
11、当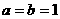 时,有
时,有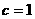 ,此时有不等式
,此时有不等式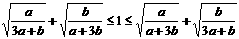 (*)先证左不等式,去分母有理化
(*)先证左不等式,去分母有理化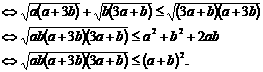
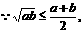
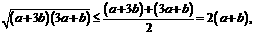
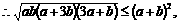 得证. 再证右不等式,去分母有理化
得证. 再证右不等式,去分母有理化 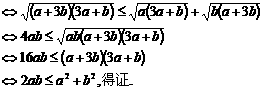

综合以上可知,不等式(*)获证. 故存在常数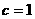 满足题意.
满足题意.
12、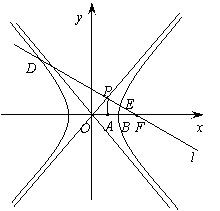 (Ⅰ)法一:
(Ⅰ)法一: 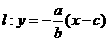 ,
,
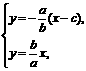 解得
解得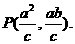
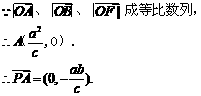

法二:同上得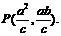
 (Ⅱ)
(Ⅱ)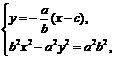
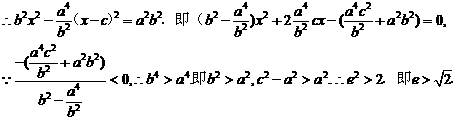
20、已知函数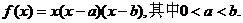
(1)设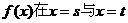 处取得极值,其中
处取得极值,其中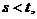 求证:
求证: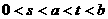 ;
;
(2)设点A(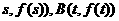 ,求证:线段AB的中点C在曲线
,求证:线段AB的中点C在曲线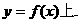
19、解关于x的不等式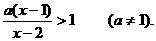
18、已知椭圆 的一条准线方程是
的一条准线方程是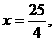 其左、右顶点分别是A、B;双曲线
其左、右顶点分别是A、B;双曲线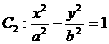 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0.
(Ⅰ)求椭圆C1的方程及双曲线C2的离心率;
(Ⅱ)在第一象限内取双曲线C2上一点P,连结AP交椭圆C1于点M,连结PB并延长交椭圆C1于点N,若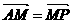 . 求证:
. 求证: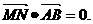
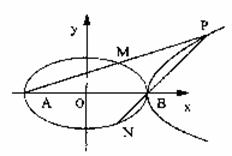
17、
 如图,过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为
如图,过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为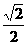 的椭圆相交于A、B两点,直线
的椭圆相交于A、B两点,直线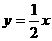 过线段AB的中点M,同时椭圆上存在一点与右焦点F关于直线l对称,求直线l和椭圆的方程.
过线段AB的中点M,同时椭圆上存在一点与右焦点F关于直线l对称,求直线l和椭圆的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com