
题目列表(包括答案和解析)
5、
若集合A={x|x=4n+1,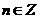 },B={x|x=4n-3,
},B={x|x=4n-3,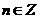 },C={x|x=8n+1,
},C={x|x=8n+1,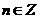 },则A,B,C的关系是( )
},则A,B,C的关系是( )
A、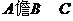 B、
B、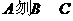 C、
C、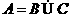 D、
D、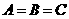
4、
已知非空集合M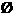 {1,2,3,4,5},且当
{1,2,3,4,5},且当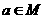 时,也有6-
时,也有6-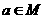 ,则集合M的个数是( )
,则集合M的个数是( )
A、3 B、4 C、5 D、6
3、
满足集合{1,2}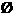 M
M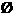 {1,2,3,4,5}的集合的个数是( )
{1,2,3,4,5}的集合的个数是( )
A、8 B、7 C、6 D、5
2、
已知A={3,a},B=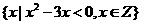 ,A
,A B={1},则A
B={1},则A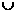 B等于( )
B等于( )
A、{1,3,a} B、{1,2,3,a} C、{1,2,3} D、{1,3}
1、
已知2a+1<0,关于x的不等式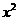 -4ax-5
-4ax-5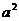 >0的解集是( )
>0的解集是( )
A、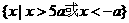 B、
B、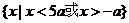
C、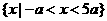 D、
D、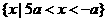
(17)(2004云南)(本小题满分12分)
数列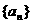 的前n项和记为Sn,已知
的前n项和记为Sn,已知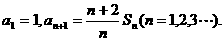 证明:
证明:
(Ⅰ)数列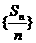 是等比数列;
是等比数列;
(Ⅱ)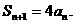
(18)(2001天津)(本小题满分12分)
设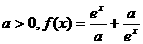 是R上的偶函数.
是R上的偶函数.
(Ⅰ)求a的值;
(Ⅱ)证明f(x)在(0,+∞)上是增函数.
(19)(2000天津)(本小题满分12分)
设函数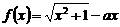 ,其中
,其中 。
。
(I)解不等式 ;
;
(II)求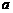 的取值范围,使函数
的取值范围,使函数 在区间
在区间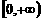 上是单调函数。
上是单调函数。
(20)(2004上海)(本题满分12分)
记函数f(x)=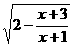 的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为B.
的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为B.
(1) 求A;
(2) 若B A, 求实数a的取值范围.
A, 求实数a的取值范围.
(21)(2002天津)(本题满分12分)已知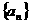 是由非负整数组成的数列,满足
是由非负整数组成的数列,满足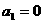 ,
,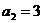 ,
,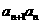 =
=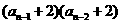 ,
,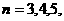 ……。
……。
(1)求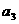 ;
;
(2)证明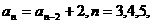 ……;
……;
(3)求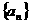 的通项公式及其前
的通项公式及其前 项和
项和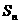 。
。
(22)(2003天津)(本小题满分14分)
设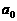 为常数,且
为常数,且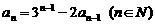 .
.
(Ⅰ)证明对任意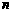 ≥1,
≥1,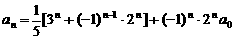 ;
;
(Ⅱ)假设对任意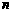 ≥1有
≥1有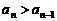 ,求
,求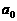 的取值范围.
的取值范围.
(附加题)(2004天津)(本小题满分15分)
已知定义在R上的函数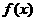 和数列
和数列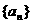 满足下列条件:
满足下列条件: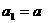 ,
,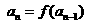 (n=2,3,4,…),
(n=2,3,4,…),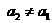 ,
,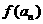 -
-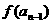 =
=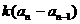 (n=2,3,4,…),其中a为常数,k为非零常数。
(n=2,3,4,…),其中a为常数,k为非零常数。
(1)令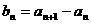
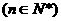 ,证明数列
,证明数列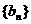 是等比数列;
是等比数列;
(2)求数列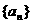 的通项公式;
的通项公式;
(3)当 时,求
时,求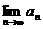 。
。
高考第一轮总复习同步试卷(十一)
集合、函数、数列
13、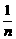 14、1
15、(0,0)、(1,1) 16、
14、1
15、(0,0)、(1,1) 16、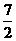
(17)本小题主要考查数列、等比数列的概念和性质,分析和推理能力,满分12分。
证明:(Ⅰ)∵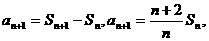
∴ 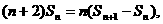 整理得
整理得 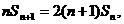
所以  故
故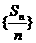 是以2为公比 的等比数列.
是以2为公比 的等比数列.
(Ⅱ)由(Ⅰ)知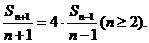 于是
于是 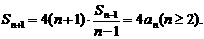
又 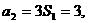 故
故 
因此对于任意正整数 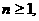 都有
都有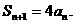
(18)本小题主要考查函数的奇偶性和单调性等基本性质,指数函数和不等式的基本性质和运算,以及综合分析问题的能力.
(I)解:依题意,对一切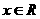 有
有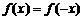 ,即
,即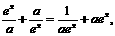
所以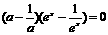 对一切
对一切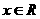 成立.
成立.
由此得到 即a2=1.
即a2=1.
又因为a>0,所以a=1.
(II)证明一:设0<x1<x2,

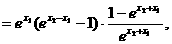
由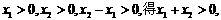
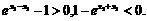
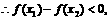 即f(x)在(0,+∞)上是增函数.
即f(x)在(0,+∞)上是增函数.
证明二:由 得
得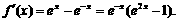
当 时,有
时,有 此时
此时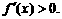
所以f(x)在(0,+∞)上是增函数.
(19)本小题主要考查不等式的解法、函数的单调性等基本知识、分类讨论的数学思想方法和运算、推理能力。满分12分。
解:(I)不等式 即
即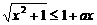 ,
,
由此可得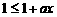 ,即
,即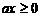 ,其中常数
,其中常数 。所以,原不等式等价于
。所以,原不等式等价于
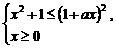 即
即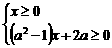 --3分
--3分
所以,当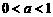 时,所给不等式的解集为
时,所给不等式的解集为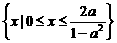 ;
;
当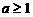 时,所给不等式的解集为
时,所给不等式的解集为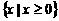 。--6分
。--6分
(II)在区间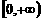 上任取
上任取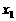 ,
,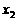 ,使得
,使得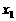 <
<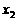 。
。
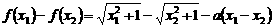
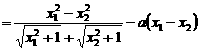
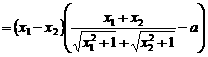 。--8分
。--8分
(i) 当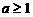 时,
时,
∵ 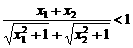 ,∴
,∴ 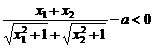 ,
,
又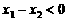 ,∴
,∴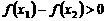 ,即
,即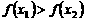 。
。
所以,当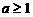 时,函数
时,函数 在区间
在区间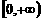 上是单调递减函数。 --10分
上是单调递减函数。 --10分
(ii)当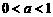 时,在区间
时,在区间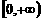 上存在两点
上存在两点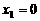 ,
,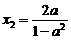 ,满足
,满足 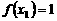 ,
,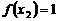 ,即
,即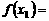
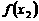 ,所以函数
,所以函数 在区间
在区间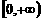 上不是单调函数。
上不是单调函数。
综上,当且仅当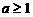 时,函数
时,函数 在区间
在区间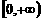 上是单调函数。--12分
上是单调函数。--12分
(20)[解](1)2-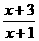 ≥0, 得
≥0, 得 ≥0, x<-1或x≥1
≥0, x<-1或x≥1
即A=(-∞,-1)∪[1,+ ∞]
(2) 由(x-a-1)(2a-x)>0, 得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a, ∴B=(2a,a+1).
∵B A, ∴2a≥1或a+1≤-1, 即a≥
A, ∴2a≥1或a+1≤-1, 即a≥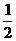 或a≤-2, 而a<1,
或a≤-2, 而a<1,
∴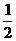 ≤a<1或a≤-2, 故当B
≤a<1或a≤-2, 故当B A时, 实数a的取值范围是(-∞,-2]∪[
A时, 实数a的取值范围是(-∞,-2]∪[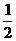 ,1)
,1)
(21)本小题主要考查数列与等差数列前n项和等基础知识,以及准确表述,分析和解决问题的能力。满分14分。
解:(1)由题设得 ,且
,且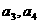 均为非负整数,所以
均为非负整数,所以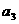 的可能的值为1、2、5、10.
的可能的值为1、2、5、10.
若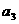 =1,则
=1,则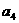 =10,
=10,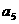 =
=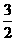 ,与题设矛盾。
,与题设矛盾。
若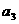 =5,则
=5,则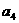 =2,
=2,  ,与题设矛盾。
,与题设矛盾。
若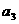 =10,则
=10,则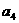 =1,
=1,  ,
,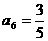 ,与题设矛盾。
,与题设矛盾。
所以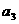 =2.
=2.
(2)用数学归纳法证明:
①当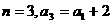 ,等式成立。
,等式成立。
②假设当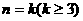 时等式成立,即
时等式成立,即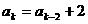 ,
,
由题设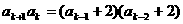
因为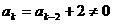
所以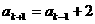
也就是说,当 时,等式
时,等式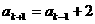 成立。
成立。
根据①②,对于所有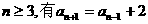 。
。
(3)由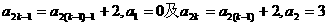 得
得
 ……。
……。
即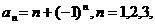 ……。
……。
所以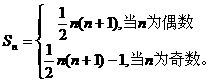
(22)本小题主要考查数列、等比数列的概念,考查数学归纳法,考查灵活运用数学知识分析问题和解决问题的能力,满分14分.
(1)证法一:(i)当n=1时,由已知a1=1-2a0,等式成立;
(ii)假设当n=k(k≥1)等式成立,则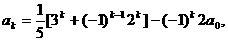
那么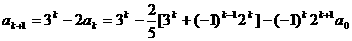
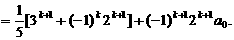
也就是说,当n=k+1时,等式也成立. 根据(i)和(ii),可知等式对任何n∈N,成立.
证法二:如果设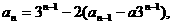 用
用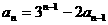 代入,可解出
代入,可解出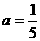 .
.
所以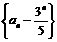 是公比为-2,首项为
是公比为-2,首项为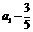 的等比数列.
的等比数列.
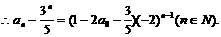 即
即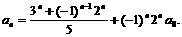
(2)解法一:由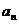 通项公式
通项公式 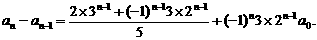
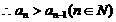 等价于
等价于 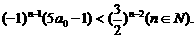 ……①
……①
(i)当n=2k-1,k=1,2,…时,①式即为 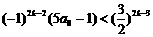
即为 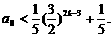 ……②
……②
②式对k=1,2,…都成立,有 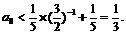
(ii)当n=2k,k=1,2,…时,①式即为 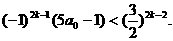
即为 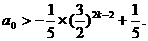 ……③
③式对k=1,2,…都成立,有
……③
③式对k=1,2,…都成立,有
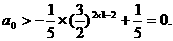 综上,①式对任意n∈N*,成立,有
综上,①式对任意n∈N*,成立,有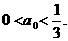
故a0的取值范围为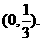
解法二:如果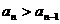 (n∈N*)成立,特别取n=1,2有
(n∈N*)成立,特别取n=1,2有 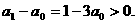
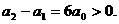 因此
因此 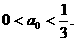 下面证明当
下面证明当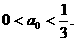 时,对任意n∈N*,
时,对任意n∈N*,
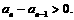 由an的通项公式
由an的通项公式 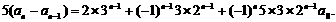
(i)当n=2k-1,k=1,2…时,
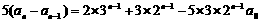


(ii)当n=2k,k=1,2…时,
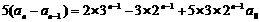

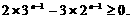
故a0的取值范围为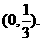
(附加题)本小题主要考查函数、数列、等比数列和极限等概念,考查灵活应用数学知识分析问题和解决问题的能力,满分12分。
(1)证明:由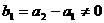 ,可得
,可得
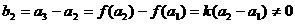 。
。
由数学归纳法可证
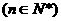 。
。
由题设条件,当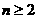 时
时
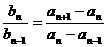

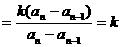
因此,数列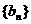 是一个公比为k的等比数列。
是一个公比为k的等比数列。
(2)解:由(1)知,
当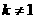 时,
时,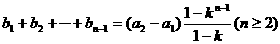
当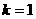 时,
时,
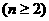 。
。
而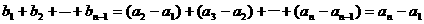
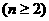
所以,当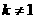 时
时
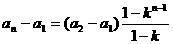
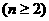 。
。
上式对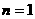 也成立。所以,数列
也成立。所以,数列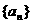 的通项公式为
的通项公式为
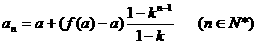
当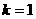 时
时
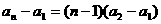
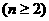 。
。
上式对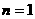 也成立,所以,数列
也成立,所以,数列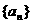 的通项公式为
的通项公式为
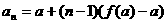
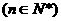 ,
,
(3)解:当 时
时

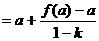
(13)(2000天津)设 是首项为1的正项数列,且
是首项为1的正项数列,且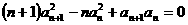 (
(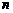 =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是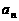 =
。
=
。
(14)(2001天津)设{an}是公比为q的等比数列,Sn是它的前n项和,若{Sn}是等差数列,则q = .
(15)(2002天津)函数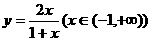 图象与其反函数图象的交点坐标为_ __。
图象与其反函数图象的交点坐标为_ __。
(16)(2002天津)已知函数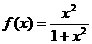 ,那么
,那么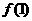 +
+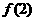 +
+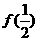 +
+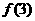 +
+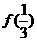 +
+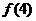 +
+ 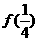 =
。
=
。
(1)(2000天津)设集合A和B都是坐标平面上的点集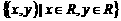 ,映射
,映射 把集合A中的元素
把集合A中的元素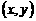 映射成集合B中的元素
映射成集合B中的元素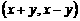 ,则在映射
,则在映射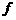 下,象
下,象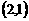 的原象是( )
的原象是( )
(A)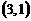 (B)
(B)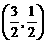 (C)
(C)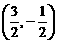 (D)
(D)
(2)(2004云南)已知集合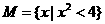 ,
,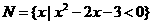 ,则集合
,则集合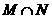 =( )
=( )
A.{ }
B.{
}
B.{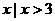 } C.{
} C.{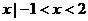 }
D. {
}
D. {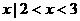 }
}
(3)(2000天津)函数 的部分图象是( )
的部分图象是( )
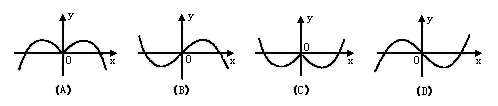
(4)(2001天津)若定义在区间(-1,0)内的函数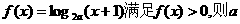 的取值范围是(
)
的取值范围是(
)
(A)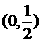 (B)
(B) (C)
(C)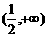 (D)
(D)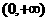
(5)(2002天津)设集合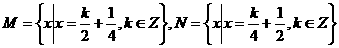 则( )
则( )
(A) (B)
(B)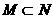 (C)
(C) (D)
(D)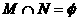
(6)(2002天津)函数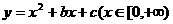 是单调函数的充要条件是( )
是单调函数的充要条件是( )
(A)b≥0 (B)b≤0 (C)b>0 (D)b<0
(7)(2002天津)已知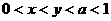 ,则有( )
,则有( )
(A)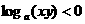 (B)
(B)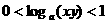
(C)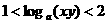 (D)
(D)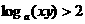
(8)(2003天津)函数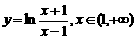 的反函数为( )
的反函数为( )
(A)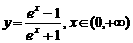 (B)
(B)
(C)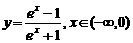 (D)
(D)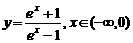
(9)(2003天津)已知方程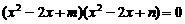 的四个根组成一个首项为
的四个根组成一个首项为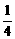 的等差数列,则
的等差数列,则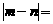 ( )
( )
(A)1
(B)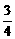 (C)
(C)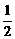 (D)
(D)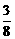
(10)(2004天津)若函数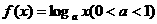 在区间
在区间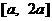 上的最大值是最小值的3倍,则a=(
)
上的最大值是最小值的3倍,则a=(
)
A. 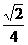 B.
B.
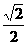 C.
C.
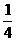 D.
D.
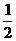
(11)(2004天津)函数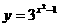 (
(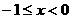 )的反函数是( )
)的反函数是( )
A. 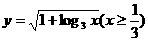 B.
B.
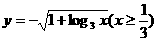
C.  D.
D.
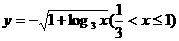
(12)(2004云南)函数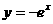 的图象( )
的图象( )
A.与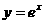 的图象关于y轴对称 B.与
的图象关于y轴对称 B.与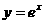 的图象关于坐标原点对称
的图象关于坐标原点对称
C.与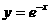 的图象关于
的图象关于 轴对称 D.与
轴对称 D.与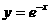 的图象关于坐标原点对称
的图象关于坐标原点对称
高考第一轮总复习同步试卷(十一)
集合、函数、数列
20、解(1)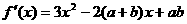 ,据题意知s,t为二次方程
,据题意知s,t为二次方程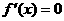 的两根…2分,
的两根…2分,
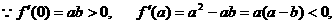
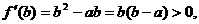
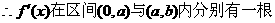 …6分
…6分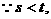
 …7分
…7分
(2)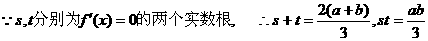 …9分
…9分
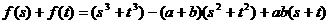
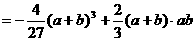
(12分)又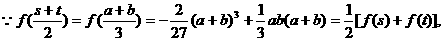
故AB中点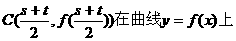 ………………………………14分
………………………………14分
17、解:由题意,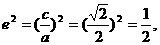 ∴
∴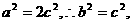 椭圆方程可设为:
椭圆方程可设为:
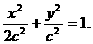 设直线l:y=k(x-1),显然k≠0,将直线方程代入椭圆方程:
设直线l:y=k(x-1),显然k≠0,将直线方程代入椭圆方程:
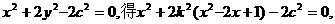 整理得:
整理得:
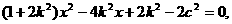 ①设交点A(
①设交点A(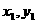 ),B(
),B(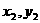 ),中点M(
),中点M(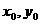 ),而中点在直线
),而中点在直线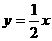 上, ∴
上, ∴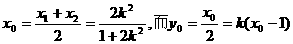
∴ ,求得:k=-1,将k=-1代入①,
,求得:k=-1,将k=-1代入①,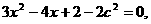
其中△>0求得 ,点F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程:∴1+2(1-c)2-2c2=0, ∴c=
,点F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程:∴1+2(1-c)2-2c2=0, ∴c=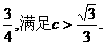 ∴所求椭圆为C:
∴所求椭圆为C:
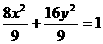 ,直线l方程为:
,直线l方程为: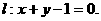
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com