
题目列表(包括答案和解析)
21.(本小题满分12分)
某俱乐部准备承办一场足球赛,预计共卖出门票2.4万张,票价有3元, 5元, 8元三种,且票价3元和5元的张数(单位:万)的积为0.6.设 是门票的总收入,经预算,扣除其他各项支出后,该俱乐部的纯收入函数为
是门票的总收入,经预算,扣除其他各项支出后,该俱乐部的纯收入函数为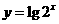 .试问三种门票分别卖出多少张时,纯收入最多?
.试问三种门票分别卖出多少张时,纯收入最多?
20.(本小题满分12分)已知数列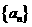 、
、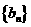 满足:
满足: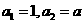 (
(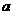 为常数),且
为常数),且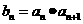 其中
其中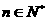 .
.
(1)若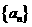 是等比数列,试求数列
是等比数列,试求数列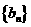 的前
的前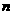 项和
项和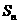 的公式;
的公式;
(2)当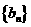 是等比数时,甲同学说:
是等比数时,甲同学说: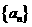 一定是等比数列;乙同学说:
一定是等比数列;乙同学说: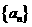 一定不是等比数列,你认为他们的说法是否正确?为什么?
一定不是等比数列,你认为他们的说法是否正确?为什么?
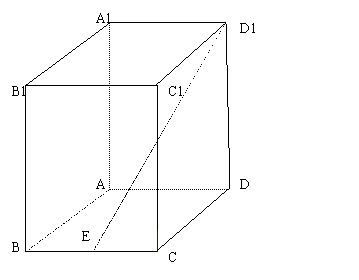
18.(本小题满分12分)如图,在棱长为1的正方体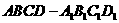 中,点E是棱BC的中点,点F是棱CD上的动点。
中,点E是棱BC的中点,点F是棱CD上的动点。
(1)试确定点F的位置,使得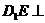 平面
平面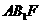 ;
;
(2)当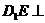 平面
平面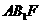 时,求二面角
时,求二面角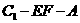 的大小(结果用反三角函数表示).
的大小(结果用反三角函数表示).

19 (本小题满分12分)把边长为4的正方形铁片的四个角各截去一个边长为 的小正方形,再将四边沿边线向上折起,做成一个无盖的方底铁盒。
的小正方形,再将四边沿边线向上折起,做成一个无盖的方底铁盒。
(1)把铁盒容积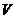 表示为
表示为 的函数
的函数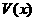 ,并指出其定义域;
,并指出其定义域;
(2)确定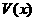 的单调区间;
的单调区间;
(3)若要求铁盒的高度 与底面正方形边长的比值不超过常数
与底面正方形边长的比值不超过常数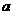 ,问
,问 取何值时,铁盒容积有最大值.
取何值时,铁盒容积有最大值.
17. (本小题满分12分)从4名男生和2名女生中任选3人参加演讲比赛,设随机变量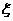 表示所选3人中女生的人数。
表示所选3人中女生的人数。
(1)求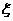 的分布列;
的分布列;
(2)求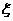 的数学期望E
的数学期望E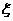 和方差D
和方差D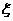 ;
;
(3)求“所选3人中女生人数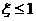 ”的概率。
”的概率。
16.老师给出一个函数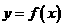 ,四个学生甲、乙、丙、丁各指出这函数的一个性质.
,四个学生甲、乙、丙、丁各指出这函数的一个性质.
甲:对于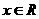 ,都有
,都有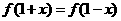 . 乙:在
. 乙:在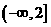 上函数递减.
上函数递减.
丙:在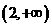 上函数递增. 丁:
上函数递增. 丁: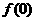 不是函数的最小值.
不是函数的最小值.
如果其中恰有三人说得正确,请写出一个这样的函数 。
。
15.用清水清洗衣服,每次都能洗去衣服上污渍的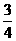 . 若想洗去衣服上的污渍
. 若想洗去衣服上的污渍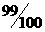 以上,则至少需清洗
以上,则至少需清洗 次.
次.
14.设函数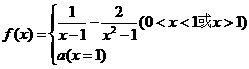 在
在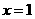 处连续,则实数
处连续,则实数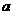 的值为
的值为 .
.
13.在数列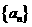 中,若
中,若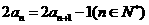 ,且
,且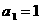 ,则
,则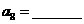 .
.
12.定义:函数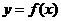
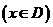 ,若存在常数T,对于任意
,若存在常数T,对于任意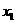
 D,存在唯一的
D,存在唯一的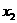
 D,使
D,使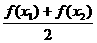 =T. 则称函数
=T. 则称函数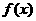 在D上的理想值为T. 已知
在D上的理想值为T. 已知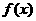 =lgx,x
=lgx,x [10,100]. 则函数
[10,100]. 则函数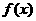 =lgx在[10,100]上的理想值为( )
=lgx在[10,100]上的理想值为( )
A. 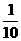 B. 10
C.
B. 10
C. 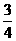 D.
D. 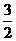
11.已知数列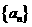 的前
的前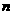 项和为
项和为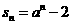 (
( 且
且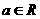 )那么数列
)那么数列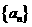 ( )
( )
A.是等比数列.
B.当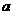 不等于1时是等比数列
不等于1时是等比数列
C.从第二项起成等比数列. D.从第二项起成等比数列或等差数列
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com