
题目列表(包括答案和解析)
22、集合A是由适合以下性质的函数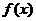 构成的:对于任意的
构成的:对于任意的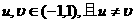 ,
,
都有
(1)分别判断函数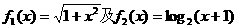 是否在集合A中?并说明理由;
是否在集合A中?并说明理由;
(2)设函数 ,求证:当
,求证:当
21、已知A(-2,0)、B(2,0),点C、点D满足
(1)求点D的轨迹方程;
(2)过点A作直线l交以A、B为焦点的椭圆于M、N两点,线段MN的中点到y轴的距离为 ,且直线l与点D的轨迹相切,求该椭圆的方程.
,且直线l与点D的轨迹相切,求该椭圆的方程.
20、已知函数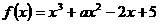 .
.
⑴若函数 在
在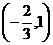 上单调递减,在
上单调递减,在 上单调递增,求实数
上单调递增,求实数 的值;
的值;
⑵是否存在正整数 ,使得
,使得 在
在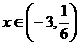 上必为单调函数?若存在,试求出
上必为单调函数?若存在,试求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
19、 在棱长为a的正方体ABCD-A1B1C1D1 中,
在棱长为a的正方体ABCD-A1B1C1D1 中,
(1)求证:平面BB1D1D⊥平面ACD1;
(2)求AA1与平面ACD1所成的角;
(3)设H为截面ACD1内一点,求H到正方体表面ADD1A1、
DCC1D1、ABCD的距离之和的最小值.
18、A有一只放有x个红球,y个白球,z个黄球的箱子(x、y、z≥0,且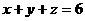 ),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
(1)用x、y、z表示B胜的概率;
(2)当A如何调整箱子中球时,才能使自己获胜的概率最大?
17、设F是椭圆 的右焦点,且椭圆上至少有21个不同的点
的右焦点,且椭圆上至少有21个不同的点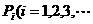 ),使|FP1|、|FP2|、|FP3|、…组成公差为d的等差数列,求公差d的取值范围.
),使|FP1|、|FP2|、|FP3|、…组成公差为d的等差数列,求公差d的取值范围.
16、从装有 个球(其中n个白球,1个黑球)的口袋中取出m个球(
个球(其中n个白球,1个黑球)的口袋中取出m个球( ,共有
,共有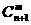 种取法. 在这
种取法. 在这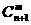 种取法中,可以分成两类:一类是取出的m个球全部为白球,共有
种取法中,可以分成两类:一类是取出的m个球全部为白球,共有 种取法;另一类是取出的m个球有
种取法;另一类是取出的m个球有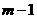 个白球和1个黑球,共有
个白球和1个黑球,共有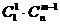 种取法. 显然
种取法. 显然 成立. 试根据上述思想化简下列式子:
成立. 试根据上述思想化简下列式子: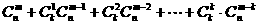 =
=
15、双曲线 右支上的点P到左焦点的距离为9,则点P的坐标为____________
右支上的点P到左焦点的距离为9,则点P的坐标为____________
14、在锐角三角形ABC中,已知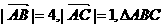 的面积为
的面积为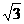 ,则
,则
, 的值为
.
的值为
.
13、已知双曲线 的一条准线与抛物线
的一条准线与抛物线 的准线重合,则m的值为
.
的准线重合,则m的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com