
题目列表(包括答案和解析)
16.(本小题满分14分)
已知向量a=(1,2),b=(-2,1),k,t为正实数,向量x= a +(t2+1)b,y=-k a+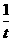 b.
b.
(1)若x⊥y,求k的最小值;
(2)是否存在正实数k,t,使x∥y?若存在,求出k的取值范围;若不存在,请说明理由.
15.(本小题满分14分)
已知Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列.
(1)求数列{an}的公比q;
(2)问a4,a7的等差中项是数列{an}中的第几项?请说明理由.
14.设函数f(x)定义域为R.若存在与x无关的正常数M,使|f(x)| ≤M|x|对一切实数x均成立,则称f(x)为有界泛函.在函数f(x)=2x,g(x)=x2,h(x)=2x,v(x)=xsinx中,属于有界泛函的有 .
13.函数f(x)=lg(x2-ax-1)在区间(1,+∞)上是单调增函数,则a的取值范围是 .
12.已知椭圆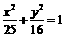 与双曲线
与双曲线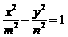 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
11.函数f(x)=6cosx+cos2x的最小值是 .
10.已知平面上点P∈{(x,y)|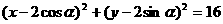 (α∈R)},则满足条件的点P在平面上所组成图形的面积是
(α∈R)},则满足条件的点P在平面上所组成图形的面积是
A.36π B.32π C.16π D.4π
第Ⅱ卷(非选择题,共100分)
9. 甲、乙两人玩猜骰子游戏.游戏的规则是:有三个骰子(每个骰子都是正方体,其六个面上分别标有数字1,2,3,4,5,6),乙先从1,2,3,4,5,6这六个数中报一个,然后由甲掷这三个骰子各一次,如果三个骰子中至少有1个骰子的向上一面的数字恰好是乙所报的这个数,那么乙获胜,否则甲获胜.若骰子任意一面向上的概率均等,则乙获胜的概率是
A.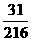 B.
B.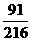 C.
C.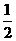 D.
D.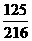
8. 定义在R上的函数f(x)对任意的实数x,满足f(x +1)=- f(x-1),则下列结论一定成立的是
A.f(x)是以4为周期的周期函数
B.f(x)是以6为周期的周期函数
C.f(x)的图象关于直线x=1对称
D.f(x)的图象关于点(1,0)对称
7.
已知sinα>0,cosα>0,且sinαcosα>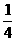 ,则α的取值范围是
,则α的取值范围是
A.(2kπ+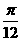 ,2kπ+
,2kπ+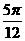 ), k∈Z
B.(kπ+
), k∈Z
B.(kπ+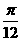 ,kπ+
,kπ+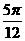 ), k∈Z
), k∈Z
C.(2kπ+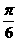 ,2kπ+
,2kπ+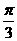 ), k∈Z D.(kπ+
), k∈Z D.(kπ+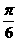 ,kπ+
,kπ+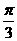 ), k∈Z
), k∈Z
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com