
题目列表(包括答案和解析)
5.不等式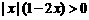 的解集是
( )
的解集是
( )
(A)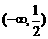 (B)
(B)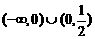 (C)
(C)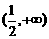 (D)
(D)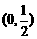
4.已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2等于 ( )
(A)-4 (B)-6 (C)-8 (D)-10
3.已知向量a=(3,4),b=(sinα,cosα),且a∥b,则tanα等于 ( )
(A)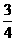 (B)
(B)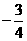 (C)
(C)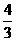 (D)
(D)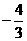
2.由“p:8+7=16,q:π>3”构成的复合命题,下列判断正确的是 ( )
(A)p或q为真,p且q为假 ,非p为真 (B)p或q为假,p且q为假 ,非p为真
(C)p或q为真,p且q为假 ,非p为假 (D)p或q为假,p且q为真 ,非p为真
1.设全集U=R,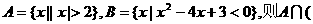
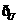 B)是 ( )
B)是 ( )
(A)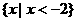 (B)
(B)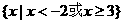
(C)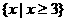 (D)
(D)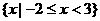
23、(14分) 已知函数f(x)=(a∈R,x≠a).
(1)f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)定义域为[a+,a+1]时,f(x)的值域为[-3,-2];
(3)设函数g(x)=x2+|(x-a)f(x)|,求g(x)的最小值.
22、(14分) 已知数列{an}的前n项和为Sn,a1=1,Sn=4an+Sn-1-an-1(n≥2,n∈N*).
(1)求证:{an}是等比数列;
(2)若bn=nan,求数列{bn}前n项和Tn;
(3)若cn=tn[n(lg3+lgt)+lgan+1](t>0)且{cn}中的每一项总小于它后面的项,求实数t的取值范围.
21、(14分) 设二项函数f(x)=ax2+bx+c(a、b、c∈R),若x1<x2<x3<x4,且x1+x4=x2+x3.
(1)试证:f(x1)+f(x4)=f(x1+x4)-2ax1x4+c;
(2)试比较x1x4与x2x3之间的大小关系;
(3)试比较f(x1)+f(x4)与f(x2)+f(x3)之间的大小关系.

20、(12分) 已知函数f(x)=a·bx的图象过点A(4,1)和B(5,1).
(1)求函数f(x)的解析式;
(2)记an=log2f(n) n∈N*,Sn是{an}前n项和,解不等式an·Sn≤0;
(3)对于(2)中的an与Sn,整数96是否是数列{anSn}中的项?若是,写出相应的项数,若不是,说明理由.
19、(12分) 已知|a|<1,|b|<1,则|a+b|+|a-b|与2的大小关系是否确定?若能确定,请指出来;若不确定,则说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com