
题目列表(包括答案和解析)
3、掌握对数的运算性质;
2、能进行对数式与指数式的互化;
1、理解对数概念;
2.利用平行平面间的距离确定
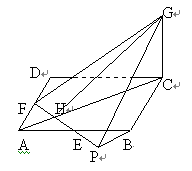
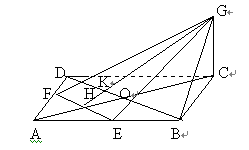
如图8,把平面EFG补成一个正四棱柱的截面所在的平面,可使题设中的点、线、面之间的位置关系更加明朗.面GMT是正四棱柱ABCD-A1B1GD1经过F、E、G的截面所在的平面.MG交BB1于N,TG交DD1于Q,作BP∥MG,交CG于P,连结DP,则有平面GTM∥平面PDB.它们之间的距离就是所求之距离.于是可以把点B平移到平面PDB上任何一个位置,哪里方便就在哪里求.
这两个平行平面的距离d又同三棱柱GQN-PDB的体积有关,所以也可以利用三棱柱的体积确定所求之距离.据此可得解法6.
解法6.三棱柱GQN-PDB的体积V=S△PDB·d,另一方面又有V=S△CDB·BN,可求得BN=2/3,CP=4/3,PB=PD=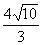 ,BD=
,BD=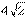 ,S△PDB=
,S△PDB=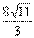 ,S△CDB=8,所以
,S△CDB=8,所以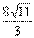 ·d=8·23,得d=
·d=8·23,得d=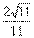 为所求之距离.
为所求之距离.
2.不直接作出所求之距离,间接求之.
(1)利用二面角的平面角.
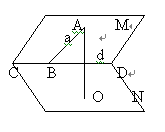
课本P.42第4题,P.46第2题、第4题给出了“二面角一个面内的一个点,它到棱的距离、到另一个面的距离与二面角的大小之间所满足的关系”.如图2,二面角M-CD-N的大小为α,A∈M,AB⊥CD,AB=a,点A到平面N的距离AO=d, 则有d=asinα. ①
①中的α也就是二面角的大小,而并不强求要作出经过AB的二面角的平面角.
解法2.如图3,过B作BP⊥EF,交FE的延长线于P,易知BP=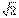 ,这就是点B到二面角C-EF-G的棱EF的距离.连结AC交EF于H,连结GH,易证∠GHC就是二面角C-EF-G的平面角.∵ GC=2,AC=4
,这就是点B到二面角C-EF-G的棱EF的距离.连结AC交EF于H,连结GH,易证∠GHC就是二面角C-EF-G的平面角.∵ GC=2,AC=4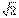 ,AH=
,AH=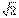 ,∴ CH=3
,∴ CH=3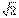 ,GH=
,GH=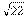 ,sin∠GHC=2/
,sin∠GHC=2/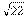 ,于是由①得所求之距离d=BP·sin∠GHC=
,于是由①得所求之距离d=BP·sin∠GHC=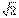 ·
·
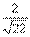 =
=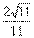 .解略.
.解略.
(2)利用斜线和平面所成的角.
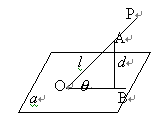
如图4,OP为平面α的一条斜线,A∈OP,OA=l,OP与α所成的角为θ,A到平面α的距离为d,则由斜线和平面所成的角的定义可知,有d=lsinθ.②
经过OP与α垂直的平面与α相交,交线与OP所成的锐角就是②中的θ,这里并不强求要作出点A在α上的射影B,连结OB得θ.
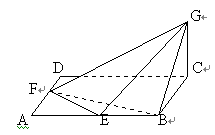
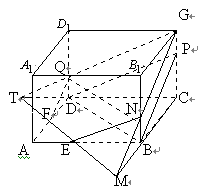
解法3.如图5,设M为FE与CB的延长线的交点,作BR⊥GM,R为垂足.又GM⊥EB,易得平面BER⊥平面EFG,ER为它们的交线,所以∠REB就是EB与平面EFG所成的角θ.由△MRB∽△MCG,可得BR=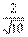 ,在Rt△REB中,∠B=90°,BR=
,在Rt△REB中,∠B=90°,BR=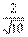 ,EB=2,所以sinθ=BR/ER=
,EB=2,所以sinθ=BR/ER=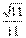 ,于是由②得所求之距离d=
,于是由②得所求之距离d=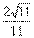 .
.
 |
 |
|
图5 |
图6 |
(3)利用三棱锥的体积公式.
解法4.如图6,设点B到平面EFG的距离为d,则三棱锥B-EFG的体积V=(1/3)S△EFG·d.另一方面又可得这个三棱锥的体积V=(1/3)S△FEB·CG,可求得S△FEB=(1/4)S△DAB=2,S△EFG=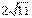 ,所以有1/3·
,所以有1/3·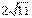 ·d=1/3·2·2,得d=
·d=1/3·2·2,得d=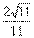 .
二、不经过该点间接确定点到平面的距离
1.利用直线到平面的距离确定
解法5.如图7,易证BD∥平面EFG,所以BD上任意一点到平面EFG的距离就是点B到平面EFG的距离.由对称思想可知,取BD中点O,求点O到平面EFG的距离较简单.AC交EF于H,交BD于O.易证平面GHC⊥平面EFG,作OK⊥HG,K为垂足,OK=
.
二、不经过该点间接确定点到平面的距离
1.利用直线到平面的距离确定
解法5.如图7,易证BD∥平面EFG,所以BD上任意一点到平面EFG的距离就是点B到平面EFG的距离.由对称思想可知,取BD中点O,求点O到平面EFG的距离较简单.AC交EF于H,交BD于O.易证平面GHC⊥平面EFG,作OK⊥HG,K为垂足,OK=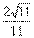 为所求之距离.
为所求之距离.
 |
 |
|
图7 |
图8 |
2.不直接作出所求之距离,间接求之.
(1)利用二面角的平面角.
课本P.42第4题,P.46第2题、第4题给出了“二面角一个面内的一个点,它到棱的距离、到另一个面的距离与二面角的大小之间所满足的关系”.如图2,二面角M-CD-N的大小为α,A∈M,AB⊥CD,AB=a,点A到平面N的距离AO=d,
则有d=asinα. ①
①中的α也就是二面角的大小,而并不强求要作出经过AB的二面角的平面角.
解法2.如图3,过B作BP⊥EF,交FE的延长线于P,易知BP=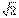 ,这就是点B到二面角C-EF-G的棱EF的距离.连结AC交EF于H,连结GH,易证∠GHC就是二面角C-EF-G的平面角.∵ GC=2,A求点到平面的距离是立体几何教学中不可忽视的一个基本问题,是近几年高考的一个热点.本文试通过对一道典型例题的多种解法的探讨,结合《立体几何》(必修本)中的概念、习题,概括出求点到平面的距离的几种基本方法.
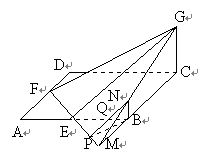
例已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在平面,且GC=2,求点B到平面EFG的距离.
一、直接通过该点求点到平面的距离
1.直接作出所求之距离,求其长.
解法1.如图1,为了作出点B到平面EFG的距离,延长FE交CB的延长线于M, 连 结GM,作BN⊥BC,交GM于N,则有BN∥CG,BN⊥平面ABCD.作BP⊥EM,交EM于P,易证平面BPN⊥平面EFG.作BQ⊥PN,垂足为Q,则BQ⊥平面EFG.于 是BQ是点B到平面EFG的距离.易知BN=2/3,BP=
,这就是点B到二面角C-EF-G的棱EF的距离.连结AC交EF于H,连结GH,易证∠GHC就是二面角C-EF-G的平面角.∵ GC=2,A求点到平面的距离是立体几何教学中不可忽视的一个基本问题,是近几年高考的一个热点.本文试通过对一道典型例题的多种解法的探讨,结合《立体几何》(必修本)中的概念、习题,概括出求点到平面的距离的几种基本方法.
例已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在平面,且GC=2,求点B到平面EFG的距离.
一、直接通过该点求点到平面的距离
1.直接作出所求之距离,求其长.
解法1.如图1,为了作出点B到平面EFG的距离,延长FE交CB的延长线于M, 连 结GM,作BN⊥BC,交GM于N,则有BN∥CG,BN⊥平面ABCD.作BP⊥EM,交EM于P,易证平面BPN⊥平面EFG.作BQ⊥PN,垂足为Q,则BQ⊥平面EFG.于 是BQ是点B到平面EFG的距离.易知BN=2/3,BP=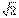 ,PN=
,PN=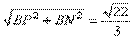 ,由BQ·PN=PB·BN,得BQ=
,由BQ·PN=PB·BN,得BQ=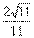 .
.
 |
 |
|
图1 |
图2 |
18.若不等式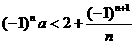 对于任意正整数
对于任意正整数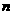 恒成立,则实数
恒成立,则实数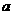 的取值范围是________.
的取值范围是________.
江苏省盐城中学2005~2006学年度第一学期期中考试
17.等差数列 的前
的前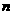 项和为
项和为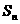 ,且
,且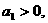 若存在自然数
若存在自然数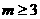 ,使得
,使得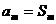 ,当
,当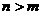 时,
时,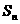 与
与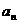 的大小关系为___________.
的大小关系为___________.
16、已知两点 ,直线
,直线 与直线
与直线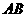 的交点为
的交点为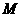 ,且
,且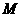 分有向线段
分有向线段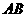 的比为
的比为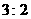 ,则
,则 =________.
=________.
15、已知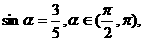 则
则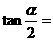 ________.
________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com