
题目列表(包括答案和解析)
(A)1800 (B)3600 (C)4320 (D)5040
(10)若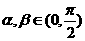 ,
,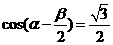 ,
,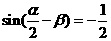 ,则
,则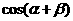 的值等于
的值等于
(A)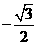 (B)
(B)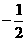 (C)
(C)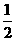 (D)
(D)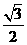
(11)设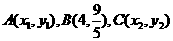 是右焦点为
是右焦点为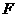 的椭圆
的椭圆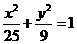 上三个不同的点,则“
上三个不同的点,则“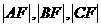 成等差数列”是“
成等差数列”是“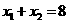 ”的
”的
(A)充要条件 (B)必要不充分条件
(C)充分不必要条件 (D)既非充分也非必要
(12)若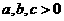 且
且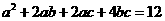 ,则
,则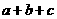 的最小值是
的最小值是
(A)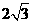 (B)3 (C)2 (D)
(B)3 (C)2 (D)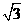
(1)已知集合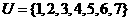 ,
,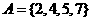 ,
,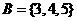 ,则
,则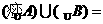
(A)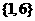 (B)
(B)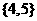 (C)
(C) (D)
(D)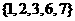
(2)在等差数列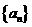 中,若
中,若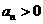 且
且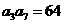 ,
,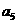 的值为
的值为
(A)2 (B)4 (C)6 (D)8
(3)以点(2,-1)为圆心且与直线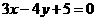 相切的圆的方程为
相切的圆的方程为
(A)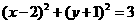 (B)
(B)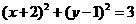
(C)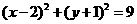 (D)
(D)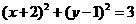
(4)若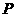 是平面
是平面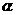 外一点,则下列命题正确的是
外一点,则下列命题正确的是
(A)过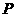 只能作一条直线与平面
只能作一条直线与平面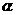 相交 (B)过
相交 (B)过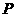 可作无数条直线与平面
可作无数条直线与平面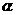 垂直
垂直
(C)过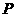 只能作一条直线与平面
只能作一条直线与平面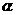 平行 (D)过
平行 (D)过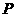 可作无数条直线与平面
可作无数条直线与平面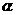 平行
平行
(5)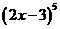 的展开式中
的展开式中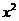 的系数为
的系数为
(A)-2160 (B)-1080 (C)1080 (D)2160
(6)设函数 的反函数为
的反函数为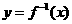 ,且
,且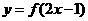 的图像过点
的图像过点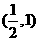 ,则
,则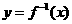 的图像必过
的图像必过
(A)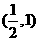 (B)
(B)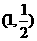 (C)
(C)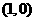 (D)
(D)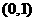
(7)某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家。为了掌握各商店的营业情况,要从中抽取一个容量为20的样本。若采用分层抽样的方法,抽取的中型商店数是
(A)2 (B)3 (C)5 (D)13
(8)已知三点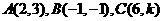 ,其中
,其中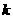 为常数。若
为常数。若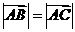 ,则
,则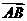 与
与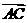 的夹角为
的夹角为
(A)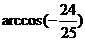 (B)
(B)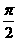 或
或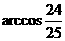
(C)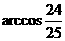 (D)
(D)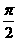 或
或
(17)(本小题13分)


(18)(本小题13分)
解:(1)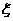 的所有可能值为0,1,2,3,4,5。
的所有可能值为0,1,2,3,4,5。
由等可能性事件的概率公式得
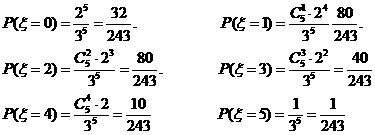
从而,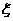 的分布列为
的分布列为
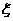 |
0 |
1 |
2 |
3 |
4 |
5 |
 |
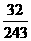 |
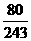 |
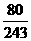 |
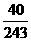 |
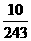 |
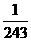 |
(II)由(I)得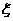 的期望为
的期望为
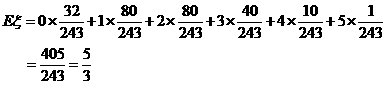
(19)(本小题13分)
(I)证:由已知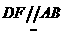 且
且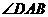 为直角。故ABFD是矩形。从而
为直角。故ABFD是矩形。从而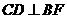 。又
。又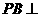 底面ABCD,
底面ABCD,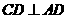 ,故由三垂线定理知
,故由三垂线定理知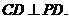 D
D 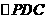 中,E、F分别为PC、CD的中点,故EF//PD,从而
中,E、F分别为PC、CD的中点,故EF//PD,从而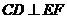 ,由此得
,由此得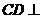 面BEF。
面BEF。
(II)连接AC交BF于G,易知G为AC的中点,连接EG,则在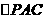 中易知EG//PA。又因PA
中易知EG//PA。又因PA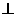 底面ABCD,故EG
底面ABCD,故EG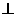 底面ABCD。在底面ABCD中,过G作GH
底面ABCD。在底面ABCD中,过G作GH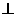 BD。垂足为H,连接EH,由三垂线定理知EH
BD。垂足为H,连接EH,由三垂线定理知EH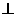 BD。从而
BD。从而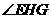 为二面角E-BD-C的平面角。
为二面角E-BD-C的平面角。
设
以下计算GH,考虑底面的平面图(如答(19)图2)。连结GD,因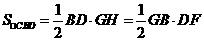
故GH=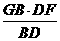 .在
.在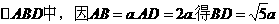 。而
。而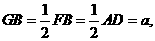
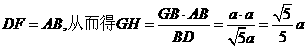 。因此,
。因此,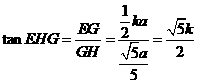 。由
。由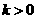 知
知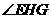 是锐角。故要使
是锐角。故要使 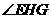
 ,必须
,必须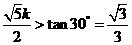 ,解之得,中的取值范围为
,解之得,中的取值范围为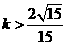
(20)(本小题13分)
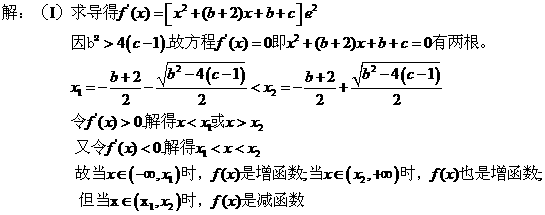
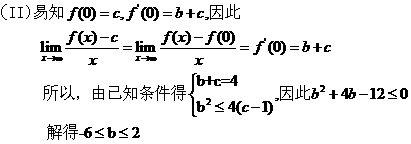
(21)题(本小题12分)
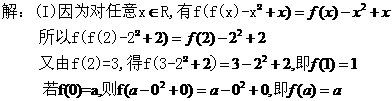

(22)(本小题12分)
证:(I)由题设及椭圆的几何性质有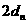
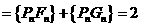 ,故
,故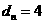 。设
。设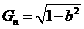 ,则右准线方程为
,则右准线方程为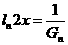 .因此,由题意
.因此,由题意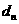 应满足
应满足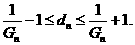 即
即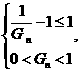 解之得:
解之得: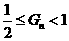 。即
。即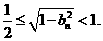 从而对任意
从而对任意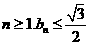
(II)高点 的坐标为
的坐标为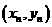 ,则由
,则由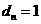 及椭圆方程易知
及椭圆方程易知
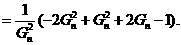 因
因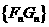
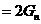 ,故
,故
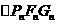 的面积为
的面积为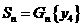 ,从而
,从而 。令
。令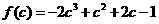 。由
。由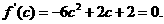 得两根
得两根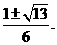 从而易知函数
从而易知函数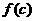 在
在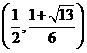 内是增函数。而在
内是增函数。而在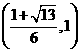 内是减函数。
内是减函数。
现在由题设取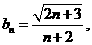 则
则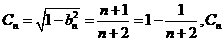 是增数列。又易知
是增数列。又易知
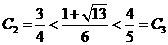 。故由前已证,知
。故由前已证,知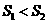 ,且
,且
(11)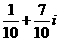 (12)
(12)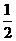 (13)
(13)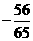 (14)
(14)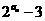
(15)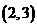 (16)
(16)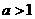
(1)D (2)B (3)A (4)C (5)A
(6)C (7)B (8)B (9)D (10)D
(17)(本小题满分13分)
设函数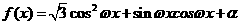 (其中
(其中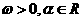 ),且
),且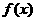 的图象在
的图象在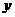 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为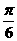 。
。
(I)求 的值。
的值。
(II)如果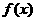 在区间
在区间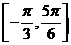 上的最小值为
上的最小值为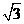 ,求
,求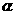 的值。
的值。
(18)(本小题满分13分)
某大夏的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为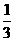 ,用
,用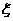 表示这5位乘客在第20层下电梯的人数,求:
表示这5位乘客在第20层下电梯的人数,求:
(I)随机变量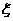 的分布列;
的分布列;
(II)随机变量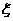 的期望;
的期望;
(19)(本小题满分13分)
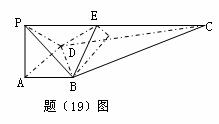 如图,在四棱锥
如图,在四棱锥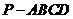 中,
中,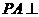 底面ABCD,
底面ABCD,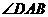 为直角,
为直角,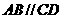 ,
,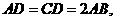 E、F分别为
E、F分别为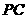 、
、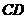 中点。
中点。
(I)试证: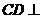 平面
平面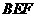 ;
;
(II)高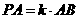 ,且二面角
,且二面角 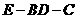 的平面角大小
的平面角大小 ,求
,求 的取值范围。
的取值范围。
(20)(本小题满分13分)
已知函数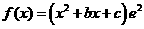 ,其中
,其中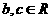 为常数。
为常数。
(I)若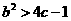 ,讨论函数
,讨论函数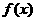 的单调性;
的单调性;
(II)若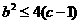 ,且
,且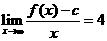 ,试证:
,试证: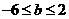
(21)(本小题满分12分)
已知定义域为R的函数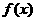 满足
满足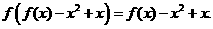
(I)若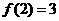 ,求
,求 ;又若
;又若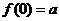 ,求
,求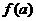 ;
;
(II)设有且仅有一个实数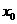 ,使得
,使得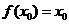 ,求函数
,求函数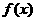 的解析表达式
的解析表达式
(22)(本小题满分12分)
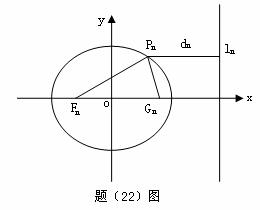 已知一列椭圆
已知一列椭圆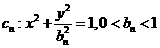 。
。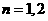 ……。若椭圆
……。若椭圆 上有一点
上有一点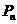 ,使
,使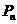 到右准线
到右准线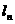 的距离
的距离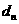 是
是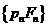 与
与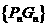 的等差中项,其中
的等差中项,其中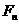 、
、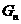 分别是
分别是 的左、右焦点。
的左、右焦点。
(I)试证: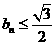
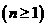 ;
;
(II)取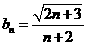 ,并用
,并用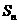 表示
表示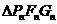 的面积,试证:
的面积,试证: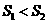 且
且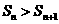
普通高等学校招生全国统一考试(重庆卷)
数学试题卷(理工农医类)答案
(11)复数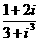 的值是
。
的值是
。
(12)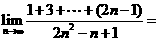 。
。
(13)已知 则
则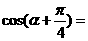 。
。
(14)在数列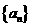 中,若
中,若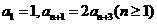 ,则该数列的通项
,则该数列的通项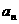
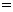 。
。
(15)设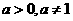 ,函数
,函数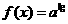 有最大值,则不等式
有最大值,则不等式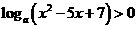 的解集为
。
的解集为
。
(16)已知变量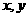 满足约束条件
满足约束条件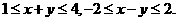 若目标函数
若目标函数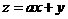 (其中
(其中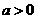 )仅在点
)仅在点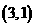 处取得最大值,则
处取得最大值,则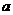 的取值范围为
。
的取值范围为
。
(1)已经集合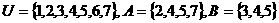 ,则
,则 =
=
(A)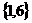 (B)
(B) (C)
(C)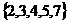 (D)
(D)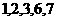
(2)在等差数列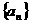 中,若
中,若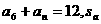 是数列的
是数列的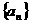 的前n项和,则
的前n项和,则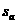 的值为( )
的值为( )
(A)48 (B)54 (C)60 (D)66
(3)过坐标原点且与圆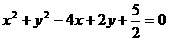 相切的直线方程为( )
相切的直线方程为( )
(A)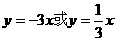 (B)
(B)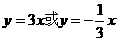
(C)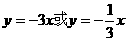 (D)
(D)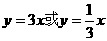
(4)对于任意的直线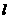 与平面
与平面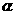 ,在平面
,在平面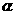 内必有直线
内必有直线 ,使
,使 与
与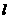 ( )
( )
(A)平行 (B)相交 (C)垂直 (D)互为异面直线
(5)若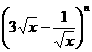 的展开式中各项系数之和为64,则展开式的常数项为( )
的展开式中各项系数之和为64,则展开式的常数项为( )
(A)-540 (B)-162 (C)162 (D)540
(6)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg),得到频率分布直方图如下:
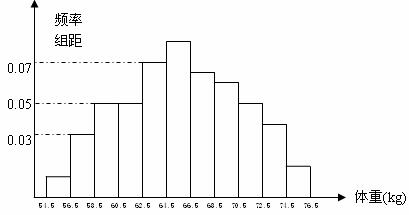
根据上图可得这100名学生中体重在 的学生人数是( )
的学生人数是( )
(A)20 (B)30 (C)40 (D)50
(7)与向量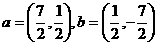 的夹角相等,且模为1的微量是( )
的夹角相等,且模为1的微量是( )
(A)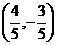 (B)
(B)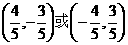
(C)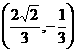 (D)
(D)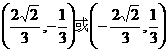
(8)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有( )
(A)30种 (B)90种 (C)180种 (D)270种
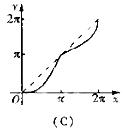
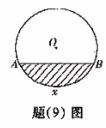 (9)如图所示,单位圆中
(9)如图所示,单位圆中 的长为
的长为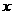 ,
,
 与弦AB所围成的弓形面积的2倍,则函数
与弦AB所围成的弓形面积的2倍,则函数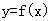 的图像是( )
的图像是( )
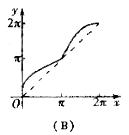
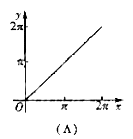
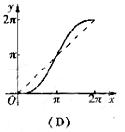
(10)若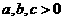 且
且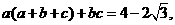 则
则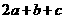 的最小值为( )
的最小值为( )
(A)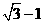 (B)
(B)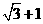 (C)
(C)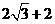 (D)
(D)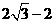
22.(本小题满分14分)
已知数列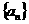 的首项
的首项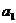 =4,前n项和为Sn ,且
=4,前n项和为Sn ,且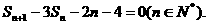
(1)求数列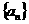 的通项公式;
的通项公式;
(2)设函数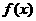 =
=

21、[理]已知中心在原点的椭圆C焦点在x轴上,一条经过点(3,-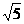 )且方向向量为
)且方向向量为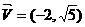 的直线l交椭圆C于A、 B两点,交x轴于M点,又
的直线l交椭圆C于A、 B两点,交x轴于M点,又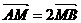

(1)求直线l方程; (2)求椭圆C长轴长取值的范围
[文]已知中心在原点的椭圆C的左焦点为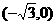 ,右顶点为(2,0).
,右顶点为(2,0).
(1)求椭圆C的方程;
(2)若直线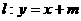 与椭圆C有两个不同的交点A和B,且
与椭圆C有两个不同的交点A和B,且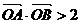 (其中O为原点), 求实数m的取值范围.
(其中O为原点), 求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com