
题目列表(包括答案和解析)
8、 设函数
设函数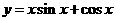 的图象上的点
的图象上的点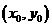 的切线的斜率为
的切线的斜率为 ,若
,若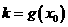 ,则函数
,则函数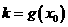 的图象大致为[ A ]
的图象大致为[ A ]
(A) (B) (C) (D)
7、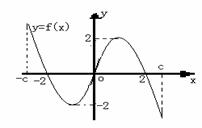
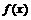 是定义在区间[-c,c]上的奇函数,其图象如图所示:令
是定义在区间[-c,c]上的奇函数,其图象如图所示:令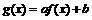 ,则下列关于函数
,则下列关于函数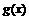 的叙述正确的是[ B
]
的叙述正确的是[ B
]
(A)若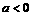 ,则函数
,则函数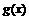 的图象关于原点对称
的图象关于原点对称
(B)若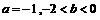 ,则方程
,则方程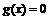 有大于2的实根
有大于2的实根
(C)若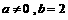 ,则方程
,则方程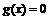 有两个实根
有两个实根
(D)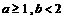 ,则方程
,则方程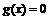 有三个实根
有三个实根
6、已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1).一质点从AB的中点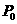 沿与AB夹角为θ的方向射到BC上的点
沿与AB夹角为θ的方向射到BC上的点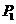 后,依次反射到CD、DA和AB上的点
后,依次反射到CD、DA和AB上的点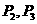 和
和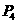 (入射角等于反射角).设
(入射角等于反射角).设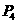 的坐标为
的坐标为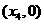 若
若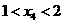 ,则tanθ的取值范围是[
C ]
,则tanθ的取值范围是[
C ]
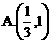
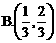
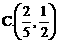
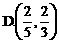
5、[理]直线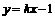 与曲线
与曲线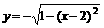 有公共点,则
有公共点,则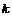 的取值范围是[ D ]
的取值范围是[ D ]
(A)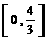 (B)
(B)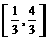 (C)
(C)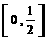 (D)
(D)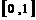
[文]已知两点A(3,2)和B(-1,4)到直线 距离相等,则m值为[ D ]
距离相等,则m值为[ D ]
(A)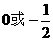 (B)
(B)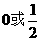 (C)
(C)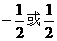 (D)
(D)
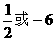
4、设向量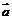 的模等于4,
的模等于4, 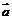 与
与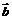 的夹角为,则
的夹角为,则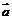 在方向
在方向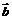 上的投影为[ B ]
上的投影为[ B ]
(A) 2 (B) -2 (C) 2 (D) -2
3、如果函数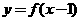 的反函数是
的反函数是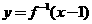 ,则下列等式中正确的是[ B ]
,则下列等式中正确的是[ B ]
(A)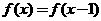 (B)
(B)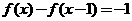
(C)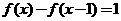 (D)
(D)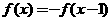
2、双曲线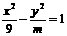 渐近线l方程为
渐近线l方程为 ,则双曲线焦点F到渐近线l的距离为[ C ]
,则双曲线焦点F到渐近线l的距离为[ C ]
(A)2 (B)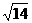 (C)
(C)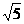 (D)2
(D)2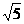
1、已知集合P={(x,y)||x|+|y|=1},Q={(x,y)|x2+y2≤1},则[A]
(A)P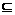 Q
(B)P=Q
(C)P
Q
(B)P=Q
(C)P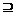 Q
(D)P∩Q=Q
Q
(D)P∩Q=Q
已知函数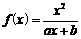 (其中
(其中 、
、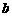 为常数).
为常数).
方程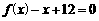 有两个实根
有两个实根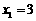 ,
,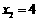 .设
.设 ,
,
解关于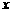 的不等式
的不等式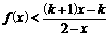 .
.
某山区的某种特产由于运输的原因,长期只能在当地销售,当地政府对该项特产的销售投资收益为:每投入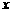 万元,可获得利润
万元,可获得利润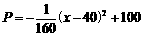 万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入
万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入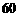 万元的销售投资,在未来
万元的销售投资,在未来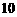 年的前
年的前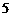 年中,每年都从
年中,每年都从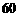 万元中拨出
万元中拨出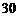 万元用于修建一条公路,
万元用于修建一条公路,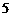 年修成,通车前该特产只能在当地销售;公路通车后的
年修成,通车前该特产只能在当地销售;公路通车后的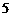 年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入
年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入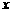 万元,可获得利润
万元,可获得利润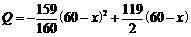 万元.问从
万元.问从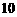 年的累积利润看,该规划方案是否可行?
年的累积利润看,该规划方案是否可行?
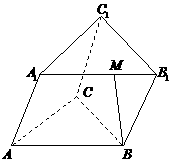
如图,三棱柱的底面是边长为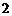 的等边三角形,侧面
的等边三角形,侧面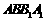 是
是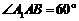 的菱形,且平面
的菱形,且平面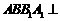 平面
平面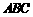 ,
,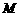 是棱
是棱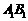 上的动点.
上的动点.
(1)当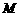 为棱
为棱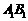 的中点时,求证:
的中点时,求证: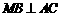 ;
;
(2)试求二面角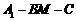 的平面角最小时三棱锥
的平面角最小时三棱锥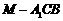 的体积.
的体积.
设函数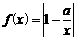 (
(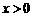 ,
,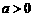 ).
).
(1)直线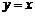 能否为函数
能否为函数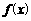 的图象的切线?若能,求出
的图象的切线?若能,求出 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(2)若方程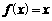 有两个不等的实根
有两个不等的实根 、
、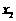 (重根只算一个根),不等式
(重根只算一个根),不等式
 对于
对于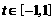 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
反面还有试题
自然状态下的鱼类是一种可再生的资源.为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响.用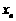 表示某鱼群在第
表示某鱼群在第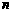 年年初的总量,
年年初的总量,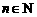 ,且
,且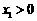 .不考虑其他因素,设在第
.不考虑其他因素,设在第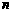 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与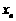 成正比,死亡量与
成正比,死亡量与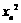 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数 、
、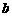 、
、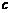 .
.
(1)求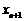 与
与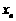 的关系式;
的关系式;
(2)猜测:当且仅当 、
、 、
、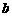 、
、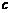 满足什么条件时,每年年初鱼群的总量保持不变(不要求证明,但要有猜测过程)?
满足什么条件时,每年年初鱼群的总量保持不变(不要求证明,但要有猜测过程)?
(3)设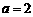 ,
,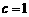 ,为保证对任意
,为保证对任意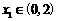 ,都有
,都有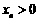 (
(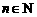 ),则捕捞强度
),则捕捞强度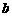 的最大允许值是多少?证明你的结论.
的最大允许值是多少?证明你的结论.
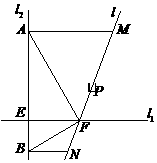 如图所示,
如图所示,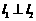 且
且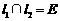 ,
,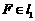 且
且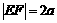 (
(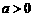 ),过
),过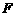 点的任意直线
点的任意直线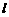 (不与
(不与 重合)交曲线
重合)交曲线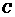 于
于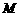 、
、 两点,
两点,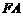 为
为 的角平分线,
的角平分线, (
(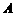 、
、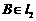 ),
),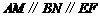 ,
,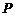 为线段
为线段 的中点.
的中点.
(1)建立适当的直角坐标系,求曲线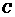 的方程;
的方程;
(2)若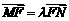 ,证明:
,证明: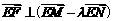 ;
;
(3)若 是奇素数(素数是指只能被
是奇素数(素数是指只能被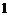 和它自身整除的正整数),且点
和它自身整除的正整数),且点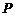 到直线
到直线 、
、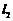 的距离均为非零整数,证明:
的距离均为非零整数,证明: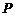 到
到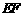 中点的距离不是整数.
中点的距离不是整数.
17 已知双曲线E的中心在原点,焦点在坐标系上,离心率e=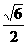 ,且双曲线过点
,且双曲线过点
P ( 2,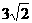 )求双曲线E的方程
)求双曲线E的方程
18 椭圆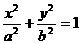 ( a>b>0 )的两焦点为F1( 0
,-c ) ,F2 (
0, c ) ( c> 0 ) ,离心率e=
( a>b>0 )的两焦点为F1( 0
,-c ) ,F2 (
0, c ) ( c> 0 ) ,离心率e=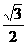 ,焦点到椭圆上的点最短距离为2 -
,焦点到椭圆上的点最短距离为2 -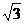 。
。
(1)求椭圆的方程;
(2)设P 、Q为椭圆与直线y=x+1的两个交点,求tan∠POQ的值。
19 设双曲线: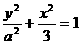 的焦点为F!、F2,离心率为2。
的焦点为F!、F2,离心率为2。
(1)求双曲线渐近线L1、 L2的方程
(2)若A、B分别为L1、 L2上的得动点,且2|AB|=5| F!F2 |,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
20 )已知点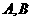 分别是椭圆
分别是椭圆 长轴的左、右端点,点
长轴的左、右端点,点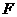 是椭圆的右焦点.点
是椭圆的右焦点.点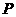 在椭圆上,且位于
在椭圆上,且位于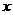 轴的上方,
轴的上方,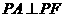 .
.
(1)求点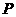 的坐标;
的坐标;
(2)设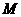 椭圆长轴
椭圆长轴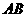 上的一点,
上的一点, 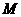 到直线
到直线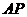 的距离等于
的距离等于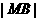 ,求椭圆上的点到点
,求椭圆上的点到点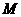 的距离
的距离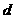 的最小值.
的最小值.
21.(14分)已知椭圆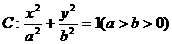 的离心率为
的离心率为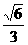 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
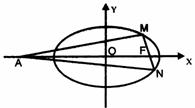
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且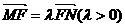 ,定点A(-4,0).
,定点A(-4,0).
(I)求证:当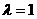 时
时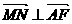 ;
;
(II)若当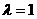 时有
时有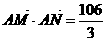 ,求椭圆C的方程;
,求椭圆C的方程;
(III)在(2)的条件下,当M、N两点在椭圆C运动时,试判断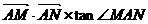 是否有最大值,若存在求出最大值,并求出这时M、N两点所在直线方程,若不存在,给出理由.
是否有最大值,若存在求出最大值,并求出这时M、N两点所在直线方程,若不存在,给出理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com