
题目列表(包括答案和解析)
⒀、已知函数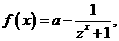 ,若
,若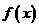 为奇函数,则
为奇函数,则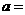 ________。
________。
⒁、已知正四棱锥的体积为12,底面对角线的长为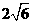 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。
⒂、设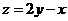 ,式中变量
,式中变量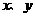 满足下列条件
满足下列条件
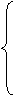
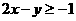
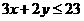
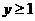
则z的最大值为_____________。
⒃、安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种。(用数字作答)
⑴、已知向量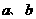 满足
满足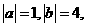 ,且
,且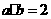 ,则
,则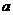 与
与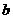 的夹角为
的夹角为
A.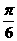 B.
B.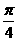 C.
C.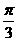 D.
D.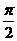
⑵、设集合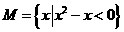 ,
,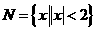 ,则
,则
A.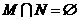 B.
B.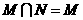
C.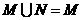 D.
D.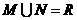
⑶、已知函数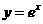 的图象与函数
的图象与函数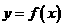 的图象关于直线
的图象关于直线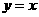 对称,则
对称,则
A.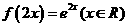 B.
B.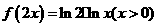
C.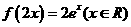 D.
D.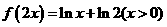
⑷、双曲线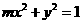 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则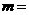
A.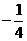 B.
B.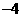 C.
C.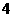 D.
D.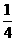
⑸、设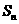 是等差数列
是等差数列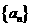 的前
的前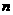 项和,若
项和,若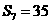 ,则
,则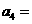
A.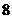 B.
B.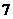 C.
C.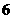 D.
D.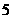
⑹、函数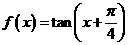 的单调增区间为
的单调增区间为
A.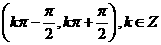 B.
B.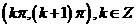
C.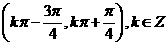 D.
D.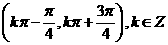
⑺、从圆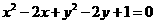 外一点
外一点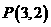 向这个圆作两条切线,则两切线夹角的余弦值为
向这个圆作两条切线,则两切线夹角的余弦值为
A.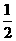 B.
B.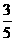 C.
C.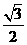 D.
D.
⑻、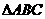 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且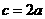 ,则
,则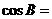
A.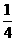 B.
B.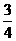 C.
C.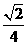 D.
D.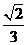
⑼、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
A.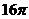 B.
B. C.
C.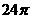 D.
D.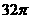
抛物线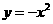 上的点到直线
上的点到直线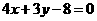 距离的最小值是
距离的最小值是
A.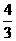 B.
B.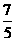 C.
C.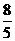 D.
D.
⑽、在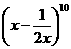 的展开式中,
的展开式中,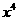 的系数为
的系数为
A.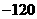 B.
B.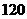 C.
C.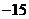 D.
D.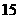
⑾、抛物线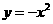 上的点到直线
上的点到直线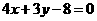 距离的最小值是
距离的最小值是
A.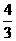 B.
B.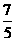 C.
C.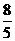 D.
D.
⑿、用长度分别为2、3、4、5、6(单位: )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为
A.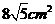 B.
B.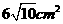 C.
C.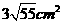 D.
D.
普通高等学校招生全国统一考试
理科数学
第Ⅱ卷
22.解: (Ⅰ)由 Sn=an-×2n+1+, n=1,2,3,… , ① 得 a1=S1= a1-×4+ 所以a1=2.
再由①有 Sn-1=an-1-×2n+, n=2,3,4,…
将①和②相减得: an=Sn-Sn-1= (an-an-1)-×(2n+1-2n),n=2,3, …
整理得: an+2n=4(an-1+2n-1),n=2,3, … , 因而数列{ an+2n}是首项为a1+2=4,公比为4的等比数列,即 : an+2n=4×4n-1= 4n, n=1,2,3, …, 因而an=4n-2n, n=1,2,3, …,
(Ⅱ)将an=4n-2n代入①得 Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
= ×(2n+1-1)(2n-1)
Tn= = × = ×( - )
所以, 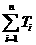 =
= 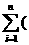 - ) = ×( - ) <
- ) = ×( - ) <
由= +得M的坐标为(x,y), 由x0,y0满足C的方程,得点M的轨迹方程为:
+ =1 (x>1,y>2)
(Ⅱ)| |2= x2+y2, y2= =4+ ,
∴| |2= x2-1++5≥4+5=9.且当x2-1= ,即x=>1时,上式取等号.
故||的最小值为3.
21.解(Ⅰ)f(x)的定义域为(-∞,1)∪(1,+∞).对f(x)求导数得 f '(x)= e-ax.
(ⅰ)当a=2时, f '(x)= e-2x, f '(x)在(-∞,0), (0,1)和(1,+ ∞)均大于0, 所以f(x)在(-∞,1), (1,+∞).为增函数.
(ⅱ)当0<a<2时, f '(x)>0, f(x)在(-∞,1), (1,+∞)为增函数.
(ⅲ)当a>2时, 0<<1, 令f '(x)=0 ,解得x1= - , x2= .
当x变化时, f '(x)和f(x)的变化情况如下表:
|
x |
(-∞, -) |
(-,) |
(,1) |
(1,+∞) |
|
f
'(x) |
+ |
- |
+ |
+ |
|
f(x) |
↗ |
↘ |
↗ |
↗ |
f(x)在(-∞, -), (,1), (1,+∞)为增函数, f(x)在(-,)为减函数.
(Ⅱ)(ⅰ)当0<a≤2时, 由(Ⅰ)知: 对任意x∈(0,1)恒有f(x)>f(0)=1.
(ⅱ)当a>2时, 取x0= ∈(0,1),则由(Ⅰ)知 f(x0)<f(0)=1
(ⅲ)当a≤0时, 对任意x∈(0,1),恒有 >1且e-ax≥1,得
f(x)= e-ax≥ >1. 综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1.
20.解: 椭圆方程可写为: + =1 式中a>b>0 , 且 得a2=4,b2=1,所以曲线C的方程为: x2+ =1 (x>0,y>0). y=2(0<x<1) y '=-
设P(x0,y0),因P在C上,有0<x0<1, y0=2, y '|x=x0= - ,得切线AB的方程为:
19.解法一: (Ⅰ)由已知l2⊥MN, l2⊥l1 , MN∩l1 =M, 可得l2⊥平面ABN.由已知MN⊥l1 , AM=MB=MN,可知AN=NB且AN⊥NB. 又AN为AC在平面ABN内的射影.
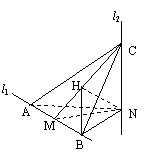 ∴AC⊥NB
∴AC⊥NB
(Ⅱ)∵Rt△CAN≌Rt△CNB, ∴AC=BC,又已知∠ACB=60°,因此△ABC为正三角形.
∵Rt△ANB≌Rt△CNB, ∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,∠NBH为NB与平面ABC所成的角.
 在Rt△NHB中,cos∠NBH=
= = .
在Rt△NHB中,cos∠NBH=
= = .
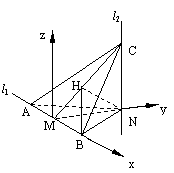
解法二: 如图,建立空间直角坐标系M-xyz.令MN=1, 则有A(-1,0,0),B(1,0,0),N(0,1,0),
(Ⅰ)∵MN是 l1、l2的公垂线, l1⊥l2, ∴l2⊥平面ABN. l2平行于z轴. 故可设C(0,1,m).于是 =(1,1,m), =(1,-1,0). ∴·=1+(-1)+0=0 ∴AC⊥NB.
(Ⅱ)∵ =(1,1,m), =(-1,1,m), ∴||=||, 又已知∠ACB=60°,∴△ABC为正三角形,AC=BC=AB=2. 在Rt△CNB中,NB=, 可得NC=,故C(0,1, ).
连结MC,作NH⊥MC于H,设H(0,λ, λ) (λ>0). ∴=(0,1-λ,-λ),
=(0,1, ). · = 1-λ-2λ=0, ∴λ= ,
∴H(0, , ), 可得=(0,, - ), 连结BH,则=(-1,, ),
∵·=0+ - =0, ∴⊥, 又MC∩BH=H,∴HN⊥平面ABC,
∠NBH为NB与平面ABC所成的角.又=(-1,1,0),
∴cos∠NBH= = =
18.解: (1)设Ai表示事件“一个试验组中,服用A有效的小鼠有i只" , i=0,1,2,
Bi表示事件“一个试验组中,服用B有效的小鼠有i只" , i=0,1,2,
依题意有: P(A1)=2×× = , P(A2)= × = . P(B0)= × = ,
P(B1)=2× × = , 所求概率为: P=P(B0·A1)+P(B0·A2)+P(B1·A2)
= × + × + × =
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3,) . P(ξ=0)=()3= , P(ξ=1)=C31××()2=
, P(ξ=2)=C32×()2× = , P(ξ=3)=( )3=
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
ξ的分布列为:
数学期望: Eξ=3× = .
17.解: 由A+B+C=π, 得 = - , 所以有cos =sin .
cosA+2cos =cosA+2sin =1-2sin2 + 2sin
=-2(sin - )2+
当sin = , 即A=时, cosA+2cos取得最大值为
⒄、(本小题满分12分)
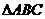 的三个内角为
的三个内角为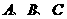 ,求当A为何值时,
,求当A为何值时,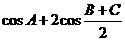 取得最大值,并求出这个最大值。
取得最大值,并求出这个最大值。
⒅、(本小题满分12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为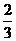 ,服用B有效的概率为
,服用B有效的概率为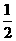 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用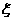 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求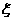 的分布列和数学期望。
的分布列和数学期望。
⒆、(本小题满分12分)
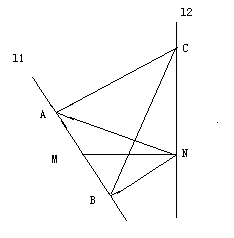
如图,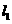 、
、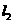 是互相垂直的异面直线,MN是它们的公垂线段。点A、B在
是互相垂直的异面直线,MN是它们的公垂线段。点A、B在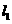 上,C在
上,C在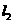 上,
上,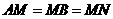 。
。
(Ⅰ)证明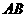 ⊥
⊥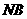 ;
;
(Ⅱ)若 ,求
,求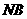 与平面ABC所成角的余弦值。
与平面ABC所成角的余弦值。
⒇、(本小题满分12分)
在平面直角坐标系 中,有一个以
中,有一个以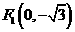 和
和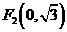 为焦点、离心率为
为焦点、离心率为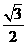 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与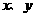 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量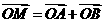 。求:
。求:
(Ⅰ)点M的轨迹方程;
(Ⅱ)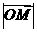 的最小值。
的最小值。
(21)、(本小题满分14分)
已知函数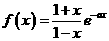 。
。
(Ⅰ)设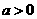 ,讨论
,讨论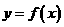 的单调性;
的单调性;
(Ⅱ)若对任意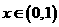 恒有
恒有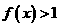 ,求
,求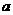 的取值范围。
的取值范围。
(22)、(本小题满分12分)
设数列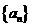 的前
的前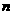 项的和
项的和
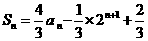 ,
,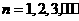
(Ⅰ)求首项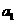 与通项
与通项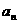 ;
;
(Ⅱ)设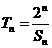 ,
,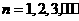 ,证明:
,证明: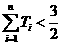
⒀、已知正四棱锥的体积为12,底面对角线的长为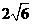 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。
⒁、设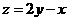 ,式中变量
,式中变量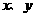 满足下列条件
满足下列条件
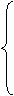
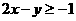
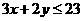
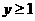
则z的最大值为_____________。
⒂、安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种。(用数字作答)
⒃、设函数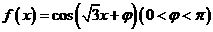 。若
。若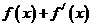 是奇函数,则
是奇函数,则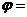 __________。
__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com