
题目列表(包括答案和解析)
4.不等式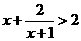 的解集是 ( )
的解集是 ( )
A. B.
B.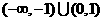
C. D.
D.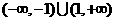
3.圆 的圆心到直线
的圆心到直线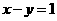 的距离为 ( )
的距离为 ( )
A.2 B.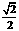 C.1
D.
C.1
D.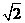
2.函数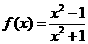 , 则
, 则 ( )
( )
A.1 B.-1 C.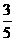 D.
D.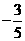
1.函数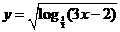 的定义域是 (
)
的定义域是 (
)
A.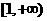 B.
B. C.[
C.[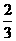 ,1] D.(
,1] D.(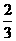 ,1
,1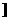
(17)已知f(x)=Asin(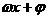 )(A>0,
)(A>0, >0,0<
>0,0<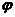 <
<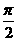 函数,且y=f(x)的最大值为2,其图象相邻两对称轴的距离为2,并过点(1,2).
函数,且y=f(x)的最大值为2,其图象相邻两对称轴的距离为2,并过点(1,2).
(1)求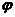 ;
;
(2)计算f(1)+f(2)+… +f(2 008).
(18)(本小题满分12分)
设函数f(x)=ax-(a+1)ln(x+1),其中a -1,求f(x)的单调区间。
-1,求f(x)的单调区间。
(19)(本小题满分12分)
如图ABC-A1B1C1,已知平面平行于三棱锥V-A1B1C1的底面ABC,等边∆ AB1C所在的平面与底面ABC垂直,且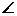 ABC=90°,设AC=2a,BC=a.
ABC=90°,设AC=2a,BC=a.
(1)求证直线B1C1是异面直线与A1C1的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角A-VB-C的大小.
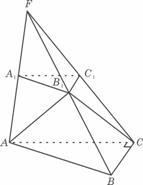
(19题图)
(20) (本小题满分12分)
袋中装着标有数学1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用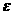 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量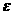 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分介于20分到40分之间的概率.
(21)(本小题满分12分)
双曲线C与椭圆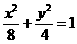 有相同的热点,直线y=
有相同的热点,直线y=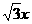 为C的一条渐近线.
为C的一条渐近线.
(1) 求双曲线C的方程;
(2)
过点P(0,4)的直线l,求双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当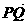 =
=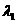
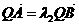 ,且
,且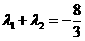 时,求Q点的坐标.
时,求Q点的坐标.
(22)(本小题满分14分)
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中=1,2,3,…
(1) 证明数列{lg(1+an)}是等比数列;
(2) 设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
(3)
记bn=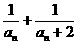 ,求{bn}数列的前项和Sn,并证明Sn+
,求{bn}数列的前项和Sn,并证明Sn+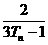 =1.
=1.
(13)若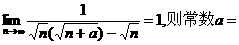 .
.
(14)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是 .
(15)如图,已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的 中点,则直线AD 与平面B1DC所成角的正弦值为 .
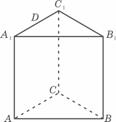
(15题图)
(16)下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①将函数y=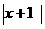 的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=
的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=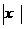
②圆x2+y2+4x-2y+1=0与直线y=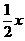 相交,所得弦长为2
相交,所得弦长为2
③若sin( +
+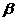 )=
)=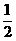 ,则sin(
,则sin( +
+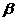 )=
)=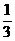 ,则tan
,则tan cot
cot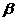 =5
=5
④如图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.
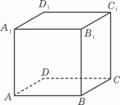
(16题图)
(1)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为
(A)0 (B)6 (C)12 (D)18
(2)函数y=1+ax(0<a<1)的反函数的图象大致是

(A) (B) (C) (D)
(3)设f(x)=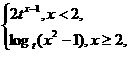
 则不等式f(x)>2的解集为
则不等式f(x)>2的解集为
(A)(1,2) (3,+∞)
(B)(
(3,+∞)
(B)( ,+∞)
,+∞)
(C)(1,2)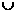 (
(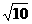 ,+∞) (D)(1,2)
,+∞) (D)(1,2)
(4)在△ABC中,角A、B、C的对边分别为a、b、c,A=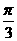 ,a=
,a=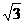 ,b=1,则c=
,b=1,则c=
(A)
1
(B)2 (C)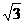 -1
(D)
-1
(D)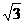
(5)设向量a=(1,2),b=(-1,1),c=(-1,-2),若表示向量4a,4b-2c,2(a-c),d的有向线段首尾相连能构成四边形,则向量d为
(A)(2,6) (B)(-2,6) (C)(2,-6) (D)(-2,-6)
(6)已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则,f(6)的值为
(A)-1 (B) 0 (C) 1 (D)2
(7)在给定椭圆中,过焦点且垂直于长轴的弦长为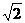 ,焦点到相应准线的距离为1,则该椭圆的离心率为
,焦点到相应准线的距离为1,则该椭圆的离心率为
(A)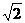 (B)
(B)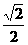 (C)
(C) 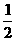 (D)
(D)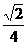
(8)设p:x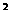 -x-20>0,q:
-x-20>0,q: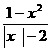 <0,则p是q的
<0,则p是q的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(9)已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素构成空间直角坐标系中点的坐标,则确定的不同点的个数为
(A)33 (B) 34 (C) 35 (D)36
(10)已知 的展开式中第三项与第五项的系数之比为-
的展开式中第三项与第五项的系数之比为-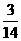 ,其中i
,其中i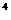 =-1,则展开式中常数项是
=-1,则展开式中常数项是
(A)-45i (B) 45i (C) -45 (D)45
(11)某公司招收男职员x名,女职员y名,x和y须满足约束条件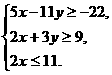 则z=10x+10y的最大值是
则z=10x+10y的最大值是
(A)80 (B) 85 (C) 90 (D)95
(12)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为
(A) (B)
(B)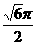 (C)
(C)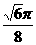 (D)
(D)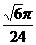
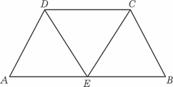
(12题图)
绝密★启用前
普通高等学校招生全国统一考试
理科数学(必修+选修II)
(17)(本小题满分12分)
在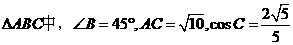 ,求
,求
(1)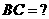
(2)若点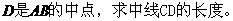
(18)(本小题满分12分)
设等比数列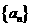 的前n项和为
的前n项和为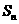 ,
,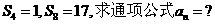
(19)(本小题满分12分)
某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品。
(I)求取6件产品中有1件产品是二等品的概率。
(II)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝的概率。
 (20)(本小题12分)
(20)(本小题12分)
如图,在直三棱柱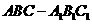 中,
中,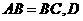 、
、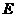 分别为
分别为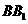 、
、 的中点。
的中点。
(I)证明:ED为异面直线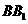 与
与 的公垂线;
的公垂线;
(II)设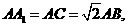 求二面角
求二面角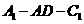 的大小
的大小
(21)(本小题满分为14分)
设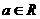 ,函数
,函数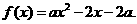 若
若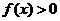 的解集为A,
的解集为A,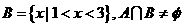 ,求实数
,求实数 的取值范围。
的取值范围。
(22)(本小题满分12分)
已知抛物线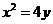 的焦点为F,A、B是抛物线上的两动点,且
的焦点为F,A、B是抛物线上的两动点,且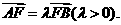 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。
(I)证明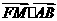 为定值;
为定值;
(II)设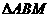 的面积为S,写出
的面积为S,写出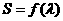 的表达式,并求S的最小值。
的表达式,并求S的最小值。
普通高等学校招生全国统一考试(全国II卷)
(13)在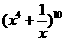 的展开式中常数项是_____。(用数字作答)
的展开式中常数项是_____。(用数字作答)
(14)圆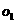 是以
是以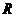 为半径的球
为半径的球 的小圆,若圆
的小圆,若圆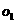 的面积
的面积 和球
和球 的表面积
的表面积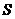 的比为
的比为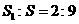 ,则圆心
,则圆心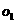 到球心
到球心 的距离与球半径的比
的距离与球半径的比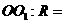 _____。
_____。
(15)过点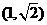 的直线
的直线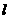 将圆
将圆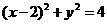 分成两段弧,当劣弧所对的圆心角最小时,直线
分成两段弧,当劣弧所对的圆心角最小时,直线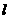 的斜率
的斜率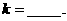
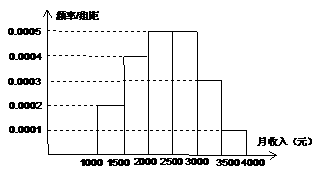 (16)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在
(16)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在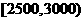 (元)月收入段应抽出_____人。
(元)月收入段应抽出_____人。
(1)已知向量 =(4,2),向量
=(4,2),向量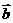 =(
=(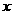 ,3),且
,3),且 //
//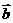 ,则
,则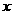 =( )
=( )
(A)9 (B)6 (C)5 (D)3
(2)已知集合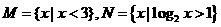 ,则
,则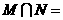 ( )
( )
(A) (B)
(B)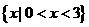 (C)
(C) (D)
(D)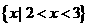
(3)函数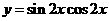 的最小正周期是( )
的最小正周期是( )
(A)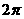 (B)
(B)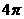 (C)
(C)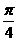 (D)
(D)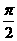
(4)如果函数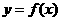 的图像与函数
的图像与函数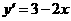 的图像关于坐标原点对称,则
的图像关于坐标原点对称,则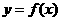 的表达式为( )
的表达式为( )
(A)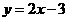 (B)
(B)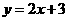 (C)
(C)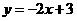 (D)
(D)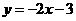
(5)已知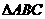 的顶点B、C在椭圆
的顶点B、C在椭圆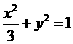 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则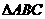 的周长是( )
的周长是( )
(A) (B)6 (C)
(B)6 (C)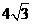 (D)12
(D)12
(6)已知等差数列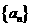 中,
中,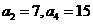 ,则前10项的和
,则前10项的和 =( )
=( )
(A)100 (B)210 (C)380 (D)400
 (7)如图,平面
(7)如图,平面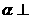 平面
平面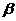 ,
,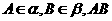 与两平面
与两平面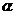 、
、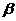 所成的角分别为
所成的角分别为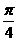 和
和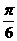 。过A、B分别作两平面交线的垂线,垂足为
。过A、B分别作两平面交线的垂线,垂足为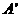 、
、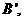 若AB=12,则
若AB=12,则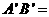 ( )
( )
(A)4 (B)6 (C)8 (D)9
(8)已知函数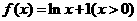 ,则
,则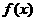 的反函数为( )
的反函数为( )
(A)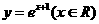 (B)
(B)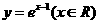
(C) (D)
(D)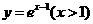
(9)已知双曲线 的一条渐近线方程为
的一条渐近线方程为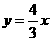 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A)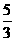 (B)
(B)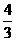 (C)
(C)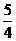 (D)
(D)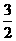
(10)若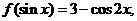 则
则 ( )
( )
(A) (B)
(B)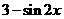 (C)
(C) (D)
(D)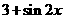
(11)过点(-1,0)作抛物线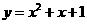 的切线,则其中一条切线为( )
的切线,则其中一条切线为( )
(A)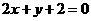 (B)
(B) (C)
(C)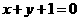 (D)
(D)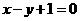
(12)5名志愿者分到3所学校支教,每个学校至少去一名志愿者,则不同的分派方法共有( )
(A)150种 (B)180种 (C)200种 (D)280种
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com