
题目列表(包括答案和解析)
3、反证法和数学归纳法都是只在特定情况下才采用的证明方法.
2、综合法的重点是正确运用有关基本不等式,即
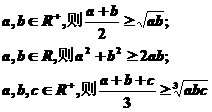
以及它们的变形形式:

注意上述式子等号成立的条件。
还有含绝对值符号的不等式的性质:

分析法(执果索因)和综合法(持因导果)不仅是不等式证明中常用的方法,也是十分重要的逻辑思维方法.它对于指导我们认识条件和结论之间的联系,设计适当的推演步骤、运算方案,使问题得到解决,起着很大的作用.
不等式证明的重点是复习、体会、运用证明中常用的几种方法.这些方法是比较法,综合法,分析法,以及反证法,数学归纳法等.有时也要涉及一点放缩法,但不要去追求那些特殊的放缩技巧.
1、比较法有两种途径,即作差法和作商法,
作差法的基本步骤是作差--变形--定号(正负号).变形是关键,通常将差式因式分解成积的形式或完全平方式与完全平方式(正数)和的形式,它是定号的依据,尤其适用具有多项式结构特征的不等式的证明,即A-B>0ÛA>B。
求商比较法的步骤是做商--变形--判断(与1比大小),即
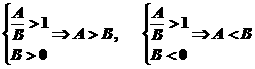
比商法适用具有乘积形式结构特征的不等式的证明。
10. 解下列不等式
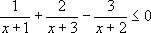
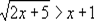
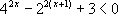
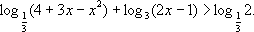
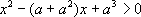
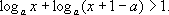
第三节 不等式的证明
9. 在下列各题的空格上填写相应不等式的解集
(1) x2-x+6>0 ______________
(2) 2x2-3x-2<0 ______________
(3) 1-x-x2£0 ______________
(4) x2+x+3³0 ______________
(5)
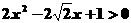 ______________
______________
(6) x2-2x+4<0 ______________
(7)
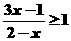 ______________
______________
(8) x2(x2-1)(x+3)³0 _____________
(9)
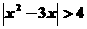 _____________
_____________
(10)
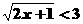 _____________
_____________
8.不等式|x+2|+|x-1|<4的解集为( ).
A.(-2,1)
B.[-2,1] C.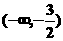 D.
D.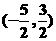
7.不等式(1-|x|)(1+x)>0的解集为( ).
A.(1,-1) B.(-¥,-1)È(-1,1)
C.(-¥,-1)È( 1,+¥) D.(-¥,-1)
6.不等式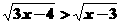 的解集为(
).
的解集为(
).
A.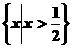 B.
B.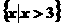
C.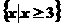 D.
D.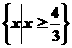
5.设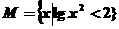 ,则M等于(
)
,则M等于(
)
A.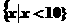 B.
B.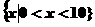
C.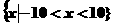 D.
D.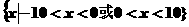
4.不等式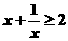 的解集为(
).
的解集为(
).
A.R
B.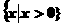
C.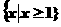 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com