
题目列表(包括答案和解析)
(13)、设常数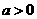 ,
,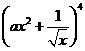 展开式中
展开式中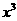 的系数为
的系数为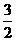 ,则
,则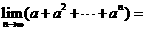 __________。
__________。
(14)、在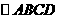 中,
中,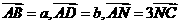 ,M为BC的中点,则
,M为BC的中点,则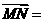 _______。(用
_______。(用 表示)
表示)
 (15)、函数
(15)、函数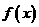 对于任意实数
对于任意实数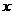 满足条件
满足条件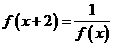 ,若
,若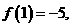 则
则 _______________。
_______________。
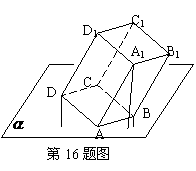
(16)、多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面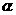 内,其余顶点在
内,其余顶点在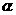 的同侧,正方体上与顶点A相邻的三个顶点到
的同侧,正方体上与顶点A相邻的三个顶点到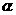 的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面
的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面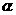 的距离可能是:
的距离可能是:
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为________________________。(写出所有正确结论的编号)
(1)、复数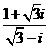 等于
等于
A.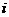 B.
B.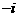 C.
C.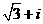 D.
D.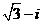
(2)、设集合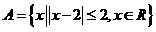 ,
,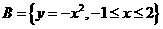 ,则
,则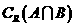 等于
等于
A.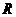 B.
B.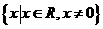 C.
C.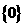 D.
D.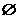
(3)、若抛物线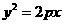 的焦点与椭圆
的焦点与椭圆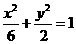 的右焦点重合,则
的右焦点重合,则 的值为
的值为
A.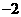 B.
B.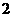 C.
C.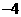 D.
D.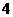
(4)、设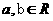 ,已知命题
,已知命题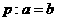 ;命题
;命题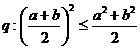 ,则
,则 是
是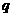 成立的
成立的
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
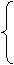
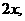
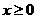
(5)、函数 的反函数是
的反函数是
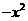 ,
, 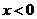
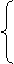
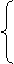
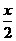 ,
, 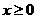
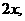
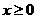
A. B.
B.
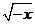 ,
, 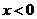
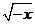 ,
, 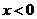
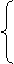
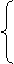
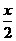 ,
, 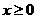
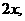
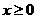
C. D.
D.
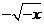 ,
, 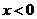
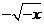 ,
, 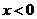
 (6)、将函数
(6)、将函数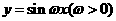 的图象按向量
的图象按向量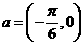 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
A.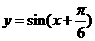
B.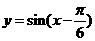
C.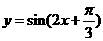
D.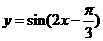
(7)、若曲线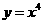 的一条切线
的一条切线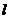 与直线
与直线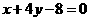 垂直,则
垂直,则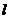 的方程为
的方程为
A.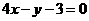
B.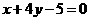
C.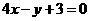
D.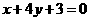
(8)、设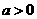 ,对于函数
,对于函数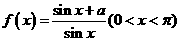 ,下列结论正确的是
,下列结论正确的是
A.有最大值而无最小值
B.有最小值而无最大值
C.有最大值且有最小值
D.既无最大值又无最小值
(9)、表面积为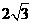 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为
A.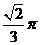 B.
B.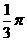 C.
C.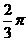 D.
D.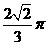
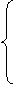
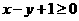 ,
,
(10)、如果实数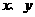 满足条件
满足条件 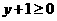 , 那么
, 那么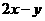 的最大值为
的最大值为
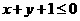 ,
,
A.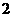 B.
B.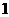 C.
C.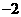 D.
D.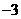
(11)、如果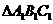 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于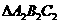 的三个内角的正弦值,则
的三个内角的正弦值,则
A.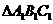 和
和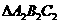 都是锐角三角形
都是锐角三角形
B.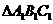 和
和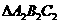 都是钝角三角形
都是钝角三角形
C.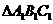 是钝角三角形,
是钝角三角形,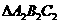 是锐角三角形
是锐角三角形
D.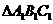 是锐角三角形,
是锐角三角形,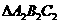 是钝角三角形
是钝角三角形
(12)、在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的概率为
A.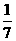 B.
B.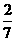 C.
C.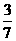 D.
D.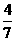
高等学校招生全国统一考试
理科数学
第Ⅱ卷(非选择题 共90分)
请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效。
22.(本小题满分14分)
已知数列{an}的前n项和Sn满足Sn-Sn-2=3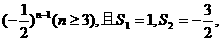 求数列{an}的通项公式.
求数列{an}的通项公式.
2005年普通高等学校招生全国统一考试(江西卷)
21.(本小题满分12分)
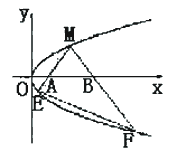
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程.
20.(本小题满分12分)
如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
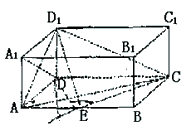 (3)AE等于何值时,二面角D1-EC-D的大小为
(3)AE等于何值时,二面角D1-EC-D的大小为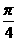 .
.
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.
18.(本小题满分12分)
已知向量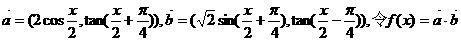 .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
17.(本小题满分12分)
已知函数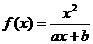 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;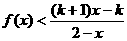 .
.
16.以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数, ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若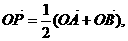 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程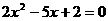 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
15.如图,在三棱锥P-ABC中,PA=PB=PC=BC,
且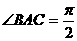 ,则PA与底面ABC所成角为
,则PA与底面ABC所成角为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com