
题目列表(包括答案和解析)
22.已知函数f(x)=-x3+ax2+b(a,b∈R)
(1)若函数y=f(x)图像上任意不同的两点连线斜率小于1,求证:-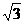 <a<
<a<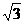
若x∈[0,1],函数y=f(x)上任一点切线斜率为k,讨论|k|≤1的充要条件
解:(1)设任意不同的两点P1(x1,y1),P2(x2,y2),且x1≠x2
则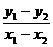 <1
(1分)
<1
(1分)
∴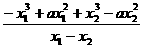 <1
<1
即-x12-x1x2-x22+a(x1+x2)<1
∴-x12+(a-x2)x1-x22+ax2-1<0 (3分)
∵x1∈R
∴Δ=(a-x2)2+4(-x22+ax2-1)<0
即-3x22+2ax2+a2-4<0
∴-3(x2-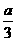 )2+
)2+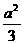 +a2-4<0
+a2-4<0
∴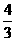 a2-4<0,∴-
a2-4<0,∴-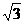 <a<
<a<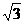 (6分)
(6分)
(2)当x∈[0,1]时,k=f′(x)=-3x2+2ax(7分)
由题意知:-1≤-3x2+2ax≤1,x∈[0,1]
即对于任意x∈[0,1],|f′(x)|≤1等价于|f′(0)|,|f′(1)|,
|f′(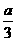 )|的值满足
)|的值满足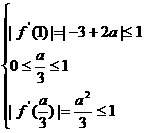
或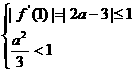 或
或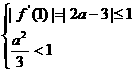 (11分)
(11分)
即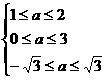 或
或 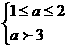 或
或 
∴1≤a≤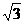
即|k|≤1的充要条件是1≤a≤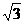
20.已知函数f(x)=x4-4x3+ax2-1在区间[0,1)上单调递增,在区间[1,2)上单调递减.
(Ⅰ)求a的值;
(Ⅱ)若点A(x0,f(x0))在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(Ⅲ)是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点.若存在,请求出实数b的值;若不存在,试说明理由.
解:(Ⅰ)由函数f(x)=x4-4x3+ax2-1,在区间[0,1)上单调递增,在区间[1,2)上单调递减,
∴x=1时,f(x)取得极大值,∴f′(1)=0. 2分
f′(x)=4x3-12x2+2ax, ∴4-12+2a=0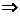 a=4. 4分
a=4. 4分
(Ⅱ)点A(x0,f(x0))关于x=1的对称点B坐标为(2-x0,f(x0)), 6分
f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1=(2-x0)2[(2-x0)-2]2-1
=x04-4x03+4x02-1=f(x0). 8分
∴点A关于直线x=1的对称点B也在函数f(x)的图象上. 9分
(Ⅲ)函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,等价于方程x4-4x3+4x2-1=bx2-1恰有3个不等实根, 10分
x4-4x3+4x2-1=bx2-1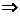 x4-4x3+(4-b)x2=0.
x4-4x3+(4-b)x2=0.
∵x=0是其中一个根,
∴方程x2-4x+(4-b)=0有两个非0不等实根. 12分
∴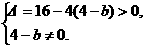 ∴b>0且b≠4. 14分
∴b>0且b≠4. 14分
19.已知偶函数f (x),对任意x1,x2∈R,恒有: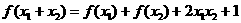 .
.
(1)求f (0),f (1),f (2)的值;
(2)求f (x);
(3)判断 在(0,+∞)上的单调性
在(0,+∞)上的单调性
解:(1) f (0) = -1,f (1) = 0,f (2) = 3;
(2)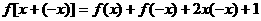 ,
,
又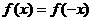 ,f (0) = -1,故
,f (0) = -1,故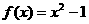 ;
;
(3)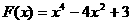 .用定义可证明
.用定义可证明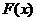 在[,+∞)上是增函数,
在[,+∞)上是增函数,
在(0,]上为减函数
18.在△ABC中,已知 .(I)若任意交换
.(I)若任意交换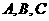 的位置,
的位置,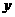 的值是否会发生变化?试证明你的结论; (II)求
的值是否会发生变化?试证明你的结论; (II)求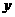 的最大值.
的最大值.
解:(I)∵ 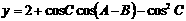

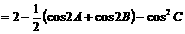
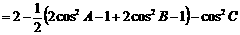
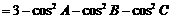
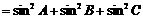 ,
,
∴ 任意交换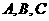 的位置,
的位置,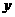 的值不会发生变化.
的值不会发生变化.
(II)将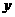 看作是关于
看作是关于 的二次函数.
的二次函数.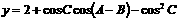
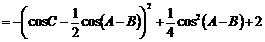 .
.
所以,当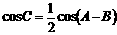 ,且
,且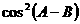 取到最大值1时,也即
取到最大值1时,也即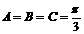 时,
时,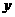 取得最大值
取得最大值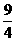 .
.
也可有如下简单解法:
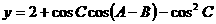
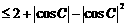
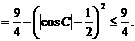
19. 已知函数: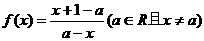 .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+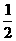 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(3)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值
解(1)证明: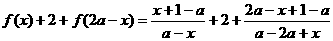
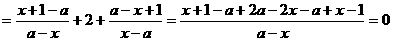 .
.
∴结论成立 ………………………………………………………………………………4’
(2)证明: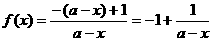
当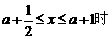 ,
,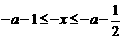 ,
,
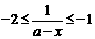 ,
,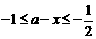 ,
,
∴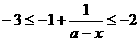 .
.
即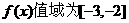 .………………………………………………………………8’
.………………………………………………………………8’
(3)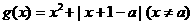
①当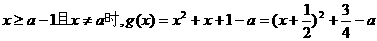 .
.
如果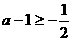 即
即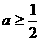 时,则函数在
时,则函数在 上单调递增,
上单调递增,
∴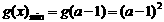 .
.
如果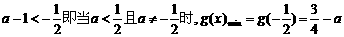 .
.
当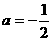 时,
时,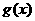 最小值不存在.……………………………………………………10’
最小值不存在.……………………………………………………10’
②当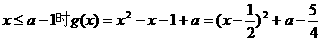 ,
,
如果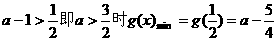 .
.
如果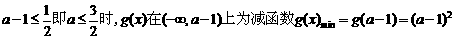 .
.
当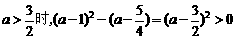 .
.
 .……………………………………………12’
.……………………………………………12’
综合得:当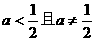 时, g(x)最小值是
时, g(x)最小值是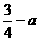 ;当
;当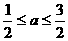 时, g(x)最小值是
时, g(x)最小值是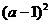 ;当
;当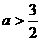 时, g(x)最小值为
时, g(x)最小值为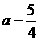 ;当
;当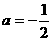 时, g(x)最小值不存在.
时, g(x)最小值不存在.
17. 已知函数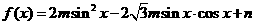 的定义域为
的定义域为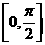 ,值域为
,值域为 .试求函数
.试求函数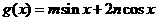 (
(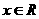 )的最小正周期和最值
)的最小正周期和最值
解: 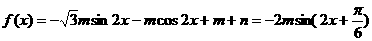
 ……2’
……2’
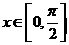
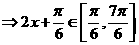
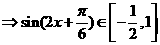 …………………………4’
…………………………4’
当 >0时,
>0时,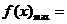
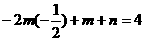 ,
,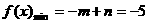
解得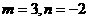 ,………………………………………………………………6’
,………………………………………………………………6’
从而,
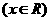 ,
,
T=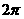 ,最大值为5,最小值为-5;………………………………………………8’
,最大值为5,最小值为-5;………………………………………………8’
当m<0时, 解得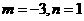 ,………………………………………………10’
,………………………………………………10’
从而, ,T=
,T=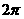 ,最大值为
,最大值为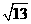 ,
,
最小值为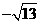 .……………………………………………………………………12
.……………………………………………………………………12
15. 若直线y=2a与函数y=|ax-1|(a>0,且a≠1)的图象有两个公共点,则a的取值范围是_ 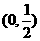 ______.
______.
14. 已知函数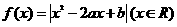 .给出下列命题:①f(x)必是偶函数;②f(0)= f(2)时,f(x)的图象必关于直线x=1对称;③若
.给出下列命题:①f(x)必是偶函数;②f(0)= f(2)时,f(x)的图象必关于直线x=1对称;③若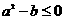 ,则f(x)在区间
,则f(x)在区间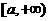 上是增函数;
上是增函数;
④f(x)有最小值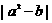 .
其中正确命题的序号是.③ .
.
其中正确命题的序号是.③ .
13. 已知二次函数f(x)= x2-3x + p-1,若在区间[0,1]内至少存在一个实数c,
使f(c)>0,则实数p的取值范围是__ (1,+∞)
16. 如右图,它满足:(1)第n行首尾两数均为n,
如右图,它满足:(1)第n行首尾两数均为n,
(2)表中的递推关系类似杨辉三角,则第n行
(n≥2)第2个数是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com