
题目列表(包括答案和解析)
6.把语文、数学、物理、历史、外语这五门课程安排在一天的五节课里,如果数学必须比历史先上,则不同的排法有
A.48 B.24 C.60 D.120
5.一组数据的方差为2,将这组数据中每个扩大为原数的2倍,则所得新的一组数据的方差是
A.16 B.8 C.4 D.2
4.给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若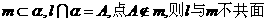 ;
;
②若m、l是异面直线, ;
;
③若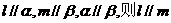 ;
;
④若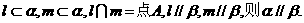
其中为假命题的是
A.① B.② C.③ D.④
3. 已知向量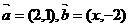 且
且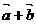 与
与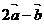 平行,则
平行,则 等于
等于
A.-6 B.6 C.4 D. -4
2.函数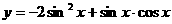 的最小正周期为
的最小正周期为
A.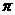 B.
B. 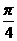 C.
C.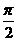 D.
D.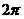
1.点(1,-1)到直线x-y+1=0的距离是
A. 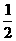 B.
B. 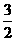 C.
C. 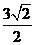 D.
D. 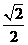
22.解:(1)∵f(a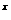 )=a
)=a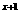 +1=a a
+1=a a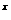 +1, ∴f(x)=ax+1, ∴a
+1, ∴f(x)=ax+1, ∴a =f(a
=f(a )-1=a a
)-1=a a ,
,
又a =b (b>0),∴
=b (b>0),∴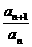 =a, (n∈N
=a, (n∈N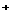 )。……3分
)。……3分
∴数列{a }为首项为b,公比为a,各项均为正的等比数列。……4分
}为首项为b,公比为a,各项均为正的等比数列。……4分
(2)①方法一:Q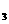 =
=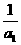 +
+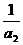 +
+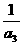 =
=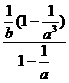 =
=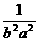
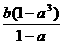 。……5分
。……5分
∵T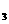 =a
=a a
a a
a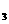 =b
=b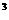 a
a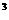 ,∴b
,∴b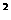 a
a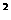 =
=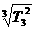 。……7分
。……7分
又S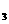 = a
= a +a
+a +a
+a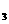 =
=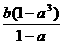 ,∴Q
,∴Q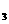 =
=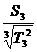 .……9分
.……9分
方法二:T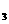 =a
=a a
a a
a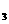 ,T
,T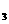 = a
= a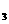 a
a a
a ∴T
∴T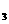
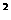 = a
= a a
a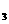 a
a
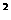 a
a a
a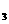 =(a
=(a a
a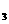 )
)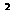
Q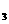 =
=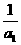 +
+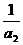 +
+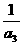 =
=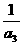 +
+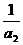 +
+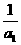 , ∴2 Q
, ∴2 Q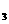 =(
=(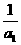 +
+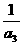 )+(
)+(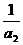 +
+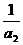 )+(
)+(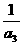 +
+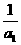 )
)
=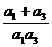 +
+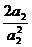 +
+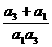 =
=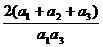 ∴Q
∴Q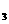 =
=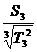 .……9分
.……9分
②Q =
=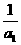 +
+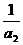 +…..+
+…..+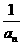 =
=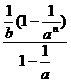 =
=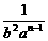
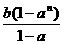 ……10分
……10分
Tn.=a a
a …. a
…. a =b
=b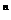 a
a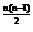 , ∴b
, ∴b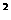 a
a =
=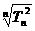 .……12分
.……12分
又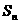 = a
= a + a
+ a +….+ a
+….+ a =
=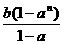 ∴Q
∴Q =
=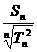 ………14分
………14分
21.解:(1)由∣ax-1∣<x ó ó
1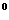 当0<a≦1时,x>
当0<a≦1时,x>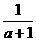 ;
;
2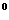
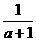 <x<
<x<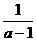 ;………5分
;………5分
∴当0<a≦1时,M={x∣x>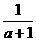 }; a>1时, M={x∣
}; a>1时, M={x∣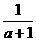 <x<
<x<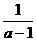 }……6分
}……6分
(2)f(x)=cos x-sin
x-sin x=
x=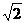 cos(
cos(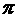 x+
x+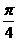 )………7分
)………7分
由2k ≦
≦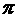 x+
x+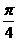 ≦2k
≦2k +
+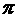 (k∈Z),得2k-
(k∈Z),得2k-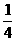 ≦x≦2k+
≦x≦2k+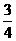 (k∈Z).
(k∈Z).
∴当0<a≦1时,f(x)在M上不单调。
当a>1时,
此时,只能k=0才有解,a≧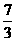 .
.
故a的最小值为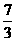 ………12分
………12分
20.解:(1)过S作SH⊥BC于H,连 DH, ∵ 面BC ⊥面ABCD,∴SH⊥面ABCD ∴∠SDH为 SD和面ABCD所成的角。……3分
⊥面ABCD,∴SH⊥面ABCD ∴∠SDH为 SD和面ABCD所成的角。……3分
在正方形BB C
C C中,M,N分别为BB
C中,M,N分别为BB ,B
,B C
C 的中点,S位MN的中点,B
的中点,S位MN的中点,B C
C =4,
=4,
∴SH=3=CH,DH=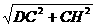 =
= ,在RTΔSHD中,tan∠SDH=
,在RTΔSHD中,tan∠SDH=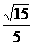 ……5分
……5分
延长B C
C 至E,使B
至E,使B C
C = C
= C E=4,连DE,ES, ∵C
E=4,连DE,ES, ∵C E平行且等于AD , ∴A C
E平行且等于AD , ∴A C ED为平行四边形。∴A C
ED为平行四边形。∴A C ∥ED,∴∠EDS为异面直线DS与A
C
∥ED,∴∠EDS为异面直线DS与A
C 所成的角。……8分
所成的角。……8分
在ΔDSE中,DS=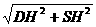 =2
=2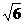 ,DE=
,DE=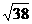 ,ES=5
,ES=5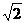 ,则cos∠EDS=
,则cos∠EDS=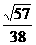 .
.
∴∠EDS=arccos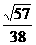 .即所求的角为arccos
.即所求的角为arccos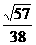 。……12分
。……12分
(附加题)连PD,过P作PF⊥面BB C
C C,垂足为F。过F作FG⊥MN于G,连结PG。
C,垂足为F。过F作FG⊥MN于G,连结PG。
由三垂线定理得PG⊥MN,d=PD.设d =PF,d
=PF,d =PG,在 RTΔPFG中,∵
=PG,在 RTΔPFG中,∵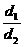 =
=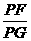 =sin∠PGF
=sin∠PGF
PG⊥MN,FG⊥MN, ∴∠PGF为二面角D-MN-C的平面角,设为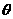 。又∵DC⊥MN, B
。又∵DC⊥MN, B C⊥MN,
C⊥MN,
∴d MN⊥面DSC. ∴∠DSC为
MN⊥面DSC. ∴∠DSC为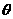 ,在RTΔDCS中,DC=
,在RTΔDCS中,DC=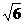 ,DS=2
,DS=2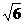 ,sin
,sin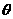 =
=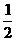 ………3分
………3分
∵d= d .∴
.∴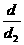 =
=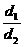 = sin
= sin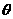 =
=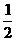 . 故
. 故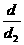 是一个定值
是一个定值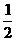 。………5分
。………5分
19.解:(1)从五名运动员中任取一名,其靶位号与参赛号相同,由C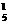 种方法,另四名运动员的靶号与参赛号均不相同的方法有9种,………2分
种方法,另四名运动员的靶号与参赛号均不相同的方法有9种,………2分
则恰有一名运动员所抽靶号与参赛号相同的概率为P=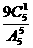 =
=
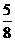 ……4分
……4分
(2)①由表可知,两人各射击一次,都未击中8环的概率为(1-0.3)(1-0.32)=0.476,
所以至少一人击中目标的概率位P=1-0.476=0.524.……8分
②1号的射击水平高。
Eξ =4×0.05+5×0.05+6×0.05+7×0.2+8×0.3+9×0.32+10×0.03
=4×0.05+5×0.05+6×0.05+7×0.2+8×0.3+9×0.32+10×0.03
Eξ =4×0.01+5×0.05+6×0.06+7×0.2+8×0.32+9×0.32+10×0.01
=4×0.01+5×0.05+6×0.06+7×0.2+8×0.32+9×0.32+10×0.01
Eξ - Eξ
- Eξ =0.02>0, ∴Eξ
=0.02>0, ∴Eξ > Eξ
> Eξ ,因此,1号运动员的射击水平高。……12分
,因此,1号运动员的射击水平高。……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com