
题目列表(包括答案和解析)
19.(本小题满分14分)
已知函数f(x)的定义域为R,对任意的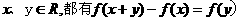 ,且当
,且当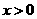 时,
时,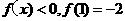 .
.
(Ⅰ)求证:函数f(x)为奇函数;(3分)
(Ⅱ)求证: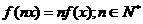 (5分)
(5分)
(Ⅲ)求函数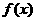 在区间[-n,n](n
在区间[-n,n](n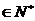 )上的最大值和最小值。(6分)
)上的最大值和最小值。(6分)
18. (本小题满分14分)
甲、乙两人比赛远距离投篮,规定每人最多投5次,谁先投中谁胜(如二人在同次都投中,则为和局,比赛结束)已知甲每次投中的概率为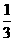 ,乙每次投中的概率为
,乙每次投中的概率为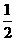 ,且每次是否投中,相互之间没有影响。
,且每次是否投中,相互之间没有影响。
(Ⅰ)求第一轮分出胜负的概率;(两人都投一次称为一轮)(3分)
(Ⅱ)求第二轮分出胜负的概率;(4分)
(Ⅲ)求乙获胜地概率。(7分)
17. (本小题满分13分)
(本小题满分13分)
已知正方体ABCD-A1B1C1D1的棱长为a,M是棱AA1的中点,
点O是对角线BD1的中点。
(Ⅰ)求证:OM是AA1和BD1的公垂线;(6分)
(Ⅱ) 过该正方体对角线BD1作截面分别交棱AA1、CC1于点P、
Q,试求截面D1PBQ面积的最小值; (7分)
16.(本小题满分12分)
已知数列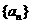 的前n项和为
的前n项和为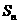 ,且向量
,且向量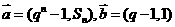 共线
共线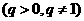 。
。
(Ⅰ)求证数列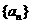 是等比数列;(6分)
是等比数列;(6分)
(Ⅱ). 求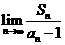 的值。(6分)
的值。(6分)
15.(本小题满分12分)
已知集合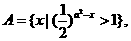 B={x||x-2|<a},若
B={x||x-2|<a},若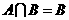 (B
(B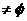 ),求实数a的取值范围.
),求实数a的取值范围.
14.函数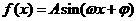
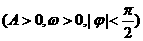 的部分图象如图所示,则有下列命题:
的部分图象如图所示,则有下列命题:
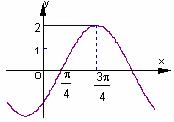 ①函数f(x)的最小正周期为
①函数f(x)的最小正周期为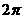 ;
;
②直线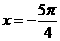 是函数f(x)的图象的一条对称轴;
是函数f(x)的图象的一条对称轴;
③点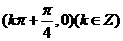 是函数f(x)图象的对称中心;
是函数f(x)图象的对称中心;
④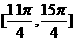 是函数f(x)的一个单调增区间.
是函数f(x)的一个单调增区间.
其中正确的命题序号是 .
13.若数列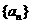 满足:
满足: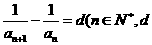 为常数),则称数列
为常数),则称数列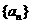 为调和数列。已知数列
为调和数列。已知数列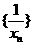 为调和数列,且
为调和数列,且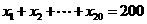 ,则
,则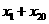 =
、
=
、
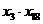 的最大值为
。
的最大值为
。
12.我省自2004年秋季开始高一学生进入新课程实验,其中课程选择的多样性是新课程的一个显著特征。设某班有50名学生,要求在《数学》选修系列Ⅳ的10个专题中每人选择2个专题学习,则共有 种选法。
11.已知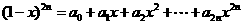 ,则
,则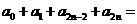 .
.
10. 已知P是椭圆
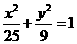 第一象限部分上一点,
第一象限部分上一点,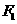 、
、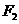 是椭圆的两个焦点,且
是椭圆的两个焦点,且
 △PF1F2的内切圆的半径为
△PF1F2的内切圆的半径为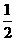 ,则点P的纵坐标为
,则点P的纵坐标为
A. 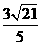 B.
B.  C
.
C
. 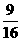 D.
D. 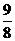
第Ⅱ卷(非选择题,共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com