
题目列表(包括答案和解析)
20.(本小题满分12分)
已知等差数列{an}的首项a1=1,且公差d>0,其第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项.
(Ⅰ)求数列{an}与{bn}的通项公式
(Ⅱ)设数列{cn}对任意自然数n均有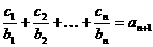 成立,
成立,
求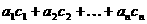 的值.
的值.
19.(本小题满分12分)
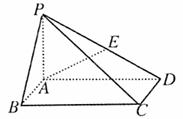
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.
(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)若E是PD的中点,求异面直线AE与PC所成角的余弦值;
(Ⅲ)在BC边上是否存在一点G,使得D点到平面PAG的距离为1,若存在,求出BG的值;若不存在,请说明理由.
18.(本小题满分12分)
甲、乙、丙三人参加某项考试,合格的概率分别为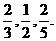
(Ⅰ)求三人中至少有两人合格的概率;
(Ⅱ)设三人中合格的人数为ξ,求ξ的数学期望.
17.(本小题满分12分)
已知函数f(x)=sin(x+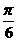 )+sin(x-
)+sin(x-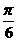 )+cosx+a(a∈R,a为常数).
)+cosx+a(a∈R,a为常数).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在[-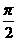 ,
,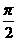 ] 上的最大值与最小值之和为
] 上的最大值与最小值之和为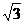 ,求实数a的值.
,求实数a的值.
16.对任意的函数f(x), g(x),在公共定义域内,规定f(x)*g(x)=min{f(x), g(x)} (min{f(x), g(x)}为f(x)与g(x)中最小的一个),若f(x)=lg(3-x), g(x)=lg ,则f(x)*g(x)的最大值为
.
,则f(x)*g(x)的最大值为
.
15.球面上有3个点,其中任意两点的球面距离都等于大圆周长的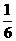 ,经过这3个点的小圆的周长为4π,则这个球的半径为
.
,经过这3个点的小圆的周长为4π,则这个球的半径为
.
14.设数列{an}是以-20为首项,并且以 为公比的无穷等比数列,则
为公比的无穷等比数列,则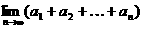
= .
13.已知x, y满足条件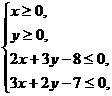 则x+y的最大值为 .
则x+y的最大值为 .
12.一张三角形纸片内有99个点,若连同原三角形的顶点共102个点中无三点共线,以这些点为三角形的顶点,把这张三角形纸片剪成小三角形,这样的小三角形共有( )个
A.300 B.156849 C.201 D.199
第Ⅱ卷(非选择题 共90分)
11.双曲线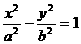 的一条准线被它的两条渐近线所截得的线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为 ( )
的一条准线被它的两条渐近线所截得的线段长度恰好等于它的一个焦点到一条渐近线的距离,则该双曲线的离心率为 ( )
A.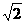 B.
B.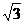 C.2 D.
C.2 D.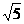
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com