
题目列表(包括答案和解析)
21、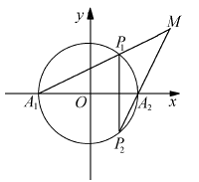 (本小题满分12分)
(本小题满分12分)
如图, 、
、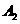 为圆
为圆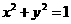 与
与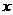 轴的两个交点,
轴的两个交点,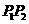 为垂直于
为垂直于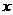 轴从弦,且
轴从弦,且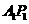 与
与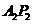 的交点为
的交点为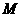 。
。
(1)
求动点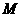 的轨迹方程;
的轨迹方程;
(2)
记动点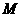 的轨迹为曲线
的轨迹为曲线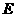 ,若过点
,若过点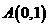 的直线
的直线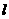 与曲线
与曲线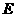 交于
交于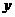 轴右边不同两点
轴右边不同两点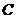 、
、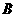 ,且
,且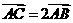 ,求直线
,求直线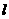 的方程。
的方程。
20、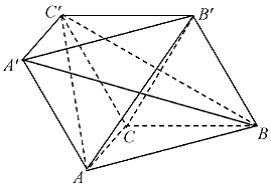 (本小题满分12分)
(本小题满分12分)
在三棱柱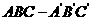 中,侧面
中,侧面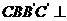 底面
底面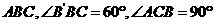 ,且
,且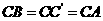 。
。
(1)
求证:平面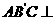 平面
平面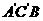 ;
;
(2)
求异面直线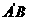 与
与 所成的角。
所成的角。
19、(本小题满分12分)
已知等差数列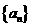 中,
中,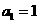 ,前10项和
,前10项和 。
。
(1)
求数列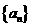 的通项公式;
的通项公式;
(2)
设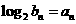 ,问
,问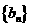 是否未等比数列;并说明理由。
是否未等比数列;并说明理由。
18、(本小题满分12分)
(理)一个口袋里有5个白球和3个黑球,任意取出一个,如果时黑球,则这个黑球不放回而另外放入一个白球,这样继续下去,直到取出的求时白球为止。求直到取到白球所需的抽取次数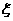 的概率分布列及
的概率分布列及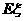 。
。
(文)在某次空战中,甲机先向乙机开火,击落乙机的概率时0.2;若乙机未被击落,就进行还击,击落甲机的概率时0.3;若甲机未被击落,则再进攻乙机,击落乙机的概率时0.4,求在这个三个回合中:
(1)甲机被击落的概率;
(2)乙机被击落的概率。
17、(本小题满分12分)
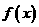 是定义在
是定义在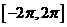 上的偶函数,当
上的偶函数,当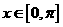 时,
时,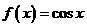 ,当
,当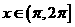 时,
时,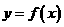 的图像时斜率为
的图像时斜率为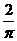 且在
且在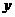 轴上的截距为
轴上的截距为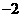 的直线在相应区间上的部分。
的直线在相应区间上的部分。
(1)
求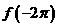 、
、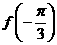 的值;
的值;
(2)
写出函数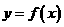 的表达式,作出其图像,并根据图像写出函数的单调区间。
的表达式,作出其图像,并根据图像写出函数的单调区间。
16、(理)从装有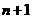 个球(其中
个球(其中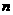 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出 个球
个球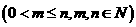 ,共有
,共有 种取法。在这
种取法。在这 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的 个球全部为白球,共有
个球全部为白球,共有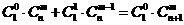 ,即有等式:
,即有等式: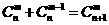 成立。试根据上述思想化简下列式子:
成立。试根据上述思想化简下列式子: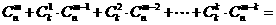 。
。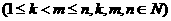 。
。
(文)对于函数的这个性质:1奇函数;2偶函数;3增函数;4减函数,函数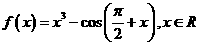 具有的性质的序号是
。(把具有的性质的序号都填上)
具有的性质的序号是
。(把具有的性质的序号都填上)
15、(理)等比数列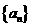 中,已知
中,已知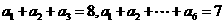 ,记
,记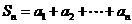 ,则
,则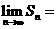 。
。
(文)等比数列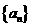 中,已知
中,已知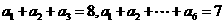 ,则公比
,则公比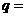 。
。
14、已知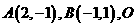 为坐标原点,动点
为坐标原点,动点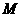 满足
满足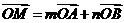 ,其中
,其中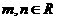 且
且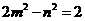 ,则
,则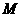 的轨迹方程为
。
的轨迹方程为
。
13、不等式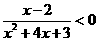 的解集是
。
的解集是
。
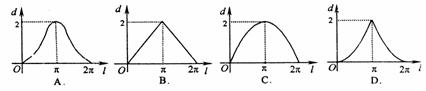
12、 如图,设点
如图,设点 是单位圆上的一定点,动点
是单位圆上的一定点,动点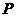 从点
从点 出发在圆上按逆时针方向旋转一周,点
出发在圆上按逆时针方向旋转一周,点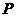 所旋转过的弧
所旋转过的弧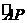 的长为
的长为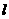 ,弦
,弦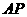 的长为
的长为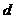 ,则函数
,则函数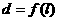 的图像大致是
的图像大致是
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com