
题目列表(包括答案和解析)
18.解:(1)由题意可得:PA.PB=(-x,-2-y).(-x,4-y)=y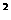 -8,
-8,
化简得x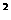 =2y……4分
=2y……4分
(2)将y=x+b 代入x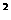 =2y中,得x
=2y中,得x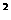 =2(x+b)整理得x
=2(x+b)整理得x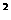 -2x-2b=0
-2x-2b=0
可知,Δ=4+8b>0,x +x
+x =2, x
=2, x x
x =-2b. ∵y
=-2b. ∵y = x
= x +b,y
+b,y = x
= x +b.
+b.
∴y y
y =(x
=(x +b)(x
+b)(x +b)= x
+b)= x x
x +b(x
+b(x +x
+x )+b
)+b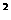 ……8分
……8分
∵OC⊥OD. ∴x x
x + y
+ y y
y =0.即b
=0.即b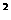 -2b=0, b=2或b=0(舍去)。即b=2…12分
-2b=0, b=2或b=0(舍去)。即b=2…12分
17.(1)∵sin(A+ 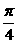 )=
)=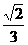 , ∴sinA + cosA=
, ∴sinA + cosA=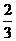 ① (sinA
+ cosA)
① (sinA
+ cosA)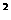 =
=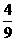 ,
,
∴2sinAcosA=-
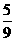 , ∵0<A<
, ∵0<A< ∴sinA > 0 , cosA < 0
∴sinA > 0 , cosA < 0
∵(sinA - cosA)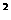 =1 - 2sinAcosA=
=1 - 2sinAcosA=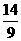 ∴sinA – cosA=
∴sinA – cosA=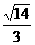 .②………4分
.②………4分
① + ②得 sinA= ………
………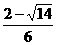 6分
6分
(2)① - ②得cosA=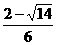 ………8分
………8分
又AC=2,AB=3, ∴BC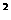 =AC
=AC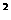 +AB
+AB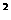 -2ABACcosA=9+2
-2ABACcosA=9+2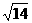
∴BC=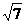 +
+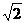 ……12分
……12分
13.f (x)=10
(x)=10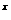 -1(x>0)14。2 15。
-1(x>0)14。2 15。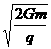 米 16。①④
米 16。①④
BACDC DCDAB AC
22.(本小题共14分)
已知函数y=f(x) (x∈R)满足:f(a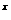 )=a
)=a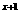 +1(a>0,且a≠1),定义数列{a
+1(a>0,且a≠1),定义数列{a }, a
}, a =b (b>0),a
=b (b>0),a =f(a
=f(a )-1(n∈N
)-1(n∈N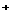 )
)
(1)
证明数列{a }为等比数列;
}为等比数列;
假设Tn.=a a
a …. a
…. a ,
, 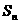 = a
= a + a
+ a +….+ a
+….+ a , Q
, Q =
=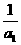 +
+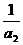 +…..+
+…..+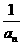 .
.
①试用T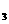 、S
、S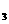 表示Q
表示Q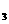 ;
;
②Q 能否写成含
能否写成含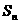 ,Tn.的表达式,若能,求出表达式;若不能,请说明理由。
,Tn.的表达式,若能,求出表达式;若不能,请说明理由。
质检二答案
21.(本小题共12分)(1)求不等式∣ax-1∣<x (a>0)的解集M;
(2)欲使函数f(x)=cos x-sin
x-sin x在(1)所得集合M上单调递减,求a的最小值。
x在(1)所得集合M上单调递减,求a的最小值。
20.(本小题共12分)如图,在长方体ABCD-A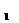 B
B C
C D
D 中,A B=
中,A B=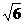 , B
, B B=BC=4,M,N分别为BB
B=BC=4,M,N分别为BB , B
, B C
C 的中点,S为线段MN的中点。
的中点,S为线段MN的中点。
(1) 求DS与平面ABCD所成角的正切值;
(2)
求直线DS与直线A C 所成的角;
所成的角;
(附加题)若点P为平面DMN上的一动点,PD=d,当点P到平面BC C B
B 的距离等于d时,d与点P到直线MN的距离之比是否为一个定值?若是,求出这个定值;若不是,说明理由。附加题供同学们选作,做对另给5分。
的距离等于d时,d与点P到直线MN的距离之比是否为一个定值?若是,求出这个定值;若不是,说明理由。附加题供同学们选作,做对另给5分。
18.(本小题共12分)已知点A(0,2)、B(0,4),动点P(x,y)满足
(1)求动点P的轨迹方程;
(2)设(1)中所求轨迹与直线y=x+b交与C,D两点,且OC⊥OD(O为原点),求b的值。
19(本小题共12分)参赛号码为1-5号的五名运动员参加射击比赛。
(1) 通过抽签将他们安排到1-5号靶位,试求恰有一名运动员所抽靶位号与其参赛号相同的概率;
(2) 记1号,2号运动员,射击的环数为ξ,(ξ所有取值为0,1,2,…,10),根据教练员提供的资料,其概率分布如下表:
|
ξ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
P |
0 |
0 |
0 |
0 |
0.05 |
0.05 |
0.05 |
0.2 |
0.3 |
0.32 |
0.03 |
P |
0 |
0 |
0 |
0 |
0.04 |
0.05 |
0.06 |
0.2 |
0.32 |
0.32 |
0.01 |
①若1,2号运动员个射击一次,求两人中至少一人命中8环的概率;
②试判断,1号,2号运动员谁的射击水平较高?并说明理由。
17.(本小题共12分)在三角形ABC中,sin( A+ 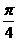 )=,AC=,AB=3.
)=,AC=,AB=3.
(1) 求sinA的值;
(2) 求BC的长。
16.对于函数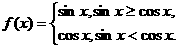 给出下列四个命题:
给出下列四个命题:
j该函数的图像关于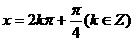 对称
对称
k当且仅当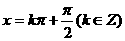 时,该函数取得最大值1;
时,该函数取得最大值1;
l该函数是以 为最小正周期的周期函数;
为最小正周期的周期函数;
m当且仅当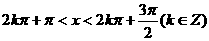 时,
时,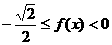 。
。
上述命题中正确的序号是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com