
题目列表(包括答案和解析)
2.已知等差数列{an}的前n项和为Sn,若a4=18-a5,则S8等于 ( )
A.18 B.36 C.54 D.72
1.设I为全集,M、N、P都是它的子集,则图中阴影部分表示的集合是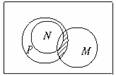
A. M∩(N∪P) B.M∩[(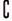 IN)∩P]
IN)∩P]
C.[(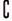 IM)∩(
IM)∩(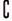 IN)]∩P D.(M∩N)∪(M∩P) ( ).
IN)]∩P D.(M∩N)∪(M∩P) ( ).
20.(本题满分14分)设定义在R上的函数f (x)=a0x4+a1x3+a2x2+a3x (a i∈R,i=0,1,2,3 ),当时,f (x)取得极大值,并且函数y=f¢ (x)的图象关于y轴对称。
(1)求f (x)的表达式;
(2)试在函数f (x)的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间[-1,1]上;
(3)求证:|f (sin x)-f (cos x) | ≤ (x∈R).
19.(本题满分14分)已知点A(0,1), x、y Î R,m≥2,设i、j为直角坐标平面内x、y轴正方向上的单位向量,若向量p = (x+m) i + y j, q = (x-m) i + y j,且 | p | -| q | = 4.
(1)求动点M (x, y )的轨迹方程,并指出方程所表示的曲线;
(2)设直线l : y = x - 3与点M的轨迹交于B、C两点,问是否存在实数m,使得 •= ?若存在,求出m的值;若不存在,试说明理由.
18.(本题满分14分)已知函数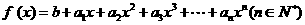 , 且y = f ( x )的图象经过点(1, n2 ),n = 1, 2 , …数列
, 且y = f ( x )的图象经过点(1, n2 ),n = 1, 2 , …数列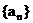 为等差数列.
为等差数列.
(1) 求数列{an}的通项公式;
(2) 当n为奇数时, 设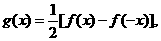 是否存在自然数m和M, 使得不等式
是否存在自然数m和M, 使得不等式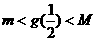 恒成立? 若存在, 求出M-m的最小值;若不存在, 请说明理由.
恒成立? 若存在, 求出M-m的最小值;若不存在, 请说明理由.
17.(本题满分14分)如图,四棱锥P -ABCD的底面是矩形,侧面PAD是 正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
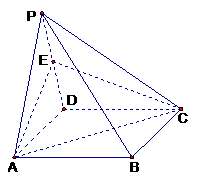 (1)试判断直线PB与平面EAC的关系(不必证明);
(1)试判断直线PB与平面EAC的关系(不必证明);
(2)求证:AE⊥平面PCD;
(3)若AD = AB,试求二面角A-PC-D的正切值;
(4)当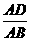 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
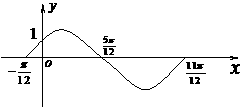
16.(本题满分12分)函数f1(x)=A sin (w x+ j ) (A>0, w >0, | j |< )的一段图象过点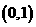 ,如图所示.
,如图所示.
(1)求函数f1 (x)的解析式;
 (2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量
(2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量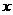 的集合.
的集合.
15.(本题满分12分)设 f (x) = |x-a|-ax,其中0<a<1为常数,
(1)解不等式 f (x)<0;
(2)试推断函数f (x)是否存在最小值,若存在,求出最小值;若不存在,说明理由。
14.两个腰长均为 1 的等腰直角△ABC1和△ABC2,C1-AB-C2是一个60° 的二面角,则点C1和C2之间的距离等于 *****。(请写出所有可能的值)
13.已知函数f (x)= ,则f (- ) = *****;(2分)
f -1(3 ) = *****。(3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com