
题目列表(包括答案和解析)
17、(本小题满分12分)
15、 16、
13、 14、
22.已知椭圆C: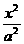 +
+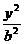 =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线
l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设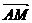 =λ
=λ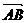 .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)若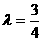 ,△PF1F2的周长为6;写出椭圆C的方程;
,△PF1F2的周长为6;写出椭圆C的方程;
(Ⅲ)确定λ的值,使得△PF1F2是等腰三角形.
 南昌十六中2006届高三数学周考试卷(6) 考试时间:2005-11-03
南昌十六中2006届高三数学周考试卷(6) 考试时间:2005-11-03

21.已知函数f(x)=-x3+3x2+ax+b在x=(1,f(1))处的切线与直线12x-y-1=0平行.
(1)求实数a的值;
(2)求f(x)的单调递减区间;
(3) 若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
20.设M是椭圆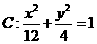 上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程.
上的一点,P、Q、T分别为M关于y轴、原点、x轴的对称点,N为椭圆C上异于M的另一点,且MN⊥MQ,QN与PT的交点为E,当M沿椭圆C运动时,求动点E的轨迹方程.
19.本小题满分12分)
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为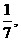 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用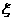 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中原有白球的个数;
(II)求随机变量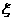 的概率分布;
的概率分布;
(III)求甲取到白球的概率.
18. (本小题满分12分)
在四棱锥P-ABCD中,AD⊥AB,CD∥AB,PD⊥底面ABCD,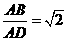 ,直线PA与底面ABCD成60°角,点M、N分别是PA、PB的中点.
,直线PA与底面ABCD成60°角,点M、N分别是PA、PB的中点.
(1) 求二面角P-MN-D的大小;
(2) 如果△CDN为直角三角形,求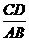 的值.
的值.
17.(本小题满分12分)
已知向量a=(1,2),b=(-2,1),k ,t为正实数,向量x=a+(t2+1)b,
y=-ka+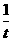 b.
b.
(1) 若x⊥y,求k的最小值;
(2) 否存在k , t ,使x∥y?若存在,求出k的取值范围;若不存在,请说明理由.
16.当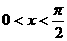 时,函数
时,函数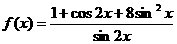 的最小值为
的最小值为 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com