
题目列表(包括答案和解析)
5.(1)
(2)存在实数λ,其值为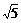
19. 湖北省部分重点中学2005年春季期中联考
湖北省部分重点中学2005年春季期中联考
如图,ABCD是矩形,PA⊥平面ABCD,
PA=AD=a,AB= a,E是线段PD上的点,F是线段AB
a,E是线段PD上的点,F是线段AB
上的点,且 .
.
(I)当 时,求直线EF与平面ABCD所成角的正弦值:
时,求直线EF与平面ABCD所成角的正弦值:
(Ⅱ)是否存在实数λ,使异面直线EF与CD所成角为
60°?若存在,试求出λ的值;若不存在,请说明
 理由.
理由.
5.(1)∵AB⊥平面BCD, ∴AB⊥CD,∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC. 3分
又 ∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF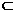 平面BEF,
平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC. 6分
(2)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC. 8分 ∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴ 10分
10分
 由AB2=AE·AC 得
由AB2=AE·AC 得
故当 时,平面BEF⊥平面ACD. 12分
时,平面BEF⊥平面ACD. 12分
5.[2005年高考重庆地区信息试卷数学试题]
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
 (Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
4.[北 京 四 中2005年数学第一次统测(理科)]
如图, 分别是正方体的棱
分别是正方体的棱 上的点.
(1)若
上的点.
(1)若 ,求证:无论点
,求证:无论点 在
在 上如何移动,总有
上如何移动,总有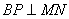 ;
(2)若
;
(2)若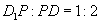 ,且
,且 平面
平面 ,求二面角
,求二面角 的大小.
的大小.
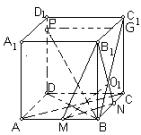 4.(I)证法一:连AC、BD,则BD⊥AC,
∵
4.(I)证法一:连AC、BD,则BD⊥AC,
∵ , ∴MN//AC,∴BD⊥MN.
又∵DD1⊥平面ABCD,∴DD1⊥MN,
∴MN⊥平面BDD1.
∵无论点P在DD1上如何移动,总有BP
, ∴MN//AC,∴BD⊥MN.
又∵DD1⊥平面ABCD,∴DD1⊥MN,
∴MN⊥平面BDD1.
∵无论点P在DD1上如何移动,总有BP 平面BDD1,
故总有MN⊥BP.
证法二:连结AC、BD,则AC⊥BD.
∵
平面BDD1,
故总有MN⊥BP.
证法二:连结AC、BD,则AC⊥BD.
∵ , ∴MN//AC,∴ MN⊥BD,又PD⊥平面ABCD,
由三垂线定理得:MN⊥PB.
(II)解法一:过P作PG⊥C1C交CC1于G,连BG交B1N于O1,
∵PB⊥平面B1MN, ∴PB⊥B1N.
又∵PG⊥平面B1BCC1, ∴ BG⊥B1N,∴ΔBB1N≌ΔBCG,
∴ BN=CG,NC=GC1,
∴BN∶NC=DP∶PD1=2∶1.
同理BM∶MA=DP∶PD1=2∶1.
设AB=3a, 则BN=2a, ∴
, ∴MN//AC,∴ MN⊥BD,又PD⊥平面ABCD,
由三垂线定理得:MN⊥PB.
(II)解法一:过P作PG⊥C1C交CC1于G,连BG交B1N于O1,
∵PB⊥平面B1MN, ∴PB⊥B1N.
又∵PG⊥平面B1BCC1, ∴ BG⊥B1N,∴ΔBB1N≌ΔBCG,
∴ BN=CG,NC=GC1,
∴BN∶NC=DP∶PD1=2∶1.
同理BM∶MA=DP∶PD1=2∶1.
设AB=3a, 则BN=2a, ∴ ,
,
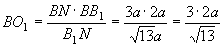 ,
连MO1,∵AB⊥平面B1BCC1, ∴ MO1⊥B1N,
∵∠MO1B就是二面角M-B1N-B的平面角,
,
连MO1,∵AB⊥平面B1BCC1, ∴ MO1⊥B1N,
∵∠MO1B就是二面角M-B1N-B的平面角,
 ,∴
,∴  .
解法二:设BD与MN相交于F,连结B1F,
∵PB⊥平面MNB1, ∴ PB⊥B1F,PB⊥MN,
∴在对角面BB1D1D内,ΔPBD∽ΔBB1F,
设BB1=DD1=3,则PD=2,
.
解法二:设BD与MN相交于F,连结B1F,
∵PB⊥平面MNB1, ∴ PB⊥B1F,PB⊥MN,
∴在对角面BB1D1D内,ΔPBD∽ΔBB1F,
设BB1=DD1=3,则PD=2, ,∴
,∴ , 即
, 即 ,故
,故 .
∵MN⊥PB,由三垂线定理得MN⊥BD,MN//AC,MN=2BF=
.
∵MN⊥PB,由三垂线定理得MN⊥BD,MN//AC,MN=2BF= , BN=2,
, BN=2,
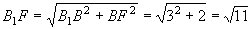 .
设二面角B-B1N-M的平面角为α,则
.
设二面角B-B1N-M的平面角为α,则 ,
,
 .
.
3.解:(1)当 (1分)
(1分)
证明:取PD中点E,则EF//CD,且
∴四边形ABFE为平行四边形. (3分)
∴BF//AE. 又AE 平面PAD ∴BF//平面PAD (4分)
平面PAD ∴BF//平面PAD (4分)
(2) 平面ABCD,
平面ABCD, 即是二面角的平
即是二面角的平
面角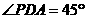 (5分)
(5分)
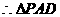 为等腰直角三角形,
为等腰直角三角形,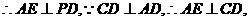
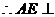 平面PCD 又BF//AE,
平面PCD 又BF//AE,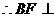 平面PCD.
平面PCD. 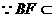 平面PBC,
平面PBC,
∴平面PCD⊥平面PBC,即二面角B-PC-D的大小为90°. (8分)
(3)在平面PCD内作EH⊥PC于点H,由平面PCD⊥平面PBC且平面PCD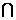
平面PBC=PC知:EH⊥平面PBC. (9分)
在 ,
,
在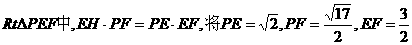 代入得:
代入得:
 即点E到平面PBC的距离为
即点E到平面PBC的距离为 (11分)
(11分)
又 点A到平面PBC的距离为
点A到平面PBC的距离为 (12分)
(12分)
3.[哈尔滨三中东北育才大连育明 天津耀华2005年四校高考模拟联考]
如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB= CD.
CD.
(I)点F在线段PC上运动,且设 为何值时,BF//平面PAD?并证明你的结论;
为何值时,BF//平面PAD?并证明你的结论;
(Ⅱ)二面角F-CD-B为45°,求二面角B-PC-D的大小;
(Ⅲ)在(Ⅱ)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.

2. 解:(1)取

 …………3分
…………3分


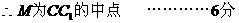
(2)取



 的距离,由
的距离,由 ,则B到面
,则B到面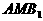 的距离为K到面
的距离为K到面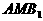 的距离的2倍 …………9分
的距离的2倍 …………9分


另法一:利用体积相等,
另法二:可利用面
2.[哈师大附中、东北师大附中、辽宁省实验中学2005年高三第二次联合考试数学试卷(理科)]
已知直三棱柱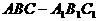 中,
中, ,AB=BC=a,
,AB=BC=a,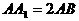 ,M为
,M为 上的点。
上的点。
(1)当M在 上的什么位置时,
上的什么位置时, 与平面
与平面 所成的角为
所成的角为 ;
;
(2)在(1)的条件下求B到平面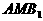 的距离。
的距离。

1.解:(I)
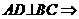 异面直线AD、BC所成角为
异面直线AD、BC所成角为 。 4分
。 4分
(II)过点P作 于E,过点E作
于E,过点E作 于F,连结PF。
于F,连结PF。

8分
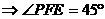 。
。
设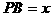 ,则在
,则在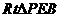 中,
中, ,
,
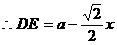
在 中,
中,
在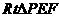 中,
中,
11分
即P、B两点间距离为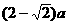 时,
时, 与
与 所在平面成
所在平面成 角。 12分
角。 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com