
题目列表(包括答案和解析)
7.圆锥的轴截面是等腰直角三角形,且圆锥的底面积为10,则它的侧面积为 ( )
 A .10 B. 10 C.
5 D.
5
A .10 B. 10 C.
5 D.
5
6.已知-9,a1,a2,-1四个实数成等差数列, -9,b1,b2,b3,-1五个实数成等比数列,则
b2(a2-a1)= ( )
A. 8 B. -8 C. ±8 D.
5.下列函数中,最小值为4的函数是 ( )
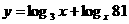
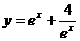
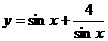
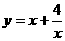
A. B. C. D.
4.设甲、乙两名射手各打了10发子弹,每发子弹击中环数如下:
甲:10,6,7,10,8,9,9,10,5,10;
乙:8,7,9,10,9,8,7,9,8,9
则甲、乙两名射手的射击技术评定情况是: ( )
A.甲比乙好 B。乙比甲好 C。甲、乙一样好 D。难以确定
3、下列各组函数中,表示同一函数的是 ( )
A.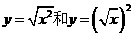 B.
B. 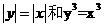
C.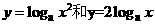 D.
D. 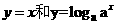
2、已知a>b,则不等式① <,② >,③ a2>b2,④ ac>bc(c≠0)中不能恒成立的是 ( )
A. 1个 B. 2个 C. 3个 D. 4个
1、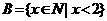
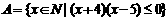 已知集合
, ,U=N,那么A∩(CUB)=(
)
已知集合
, ,U=N,那么A∩(CUB)=(
)
A . {1,2,3,4,5} B . {2,3,4,5}
C . {3,4,5} D . {x|1<x≤5}
21. 设关于x的一元二次方程2x2-ax-2=0的两根的α、β(α<β),函数f(x)=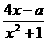
⑴求f(α)·f(β)的值;⑵证明f(x)是[α,β]的增函数;
(3)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小?
解:⑴ f(α)f(β)=-4
⑵设α≤x1<x2≤β,f(x1)-f(x2)=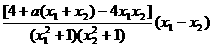 17. 已知函数
17. 已知函数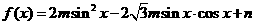 的定义域为
的定义域为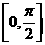 ,值域为
,值域为 .试求函数
.试求函数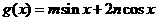 (
(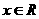 )的最小正周期和最值
)的最小正周期和最值
解: 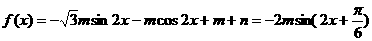
 ……2’
……2’
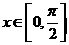
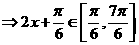
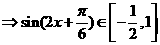 …………………………4’
…………………………4’
当 >0时,
>0时,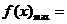
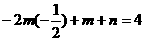 ,
,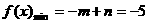
解得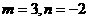 ,………………………………………………………………6’
,………………………………………………………………6’
从而,
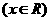 ,
,
T=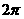 ,最大值为5,最小值为-5;………………………………………………8’
,最大值为5,最小值为-5;………………………………………………8’
当m<0时, 解得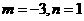 ,………………………………………………10’
,………………………………………………10’
从而, ,T=
,T=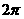 ,最大值为
,最大值为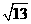 ,
,
最小值为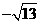 .……………………………………………………………………12
.……………………………………………………………………12
20. 已知集合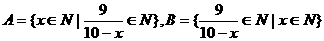 ,试问集合A与B共有几个相同的元素,并写出由这些“相同元素”组成的集合.
,试问集合A与B共有几个相同的元素,并写出由这些“相同元素”组成的集合.
解:因为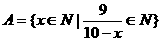 ,所以
,所以 ,
,
因为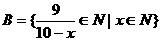 ,所以
,所以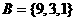 ,
,
所以A、B有两个公共元素,由这些“相同元素”组成的集合是{1,9}.
19. 已知函数: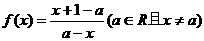 .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+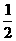 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(3)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值 .
解(1)证明: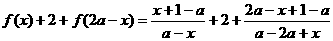
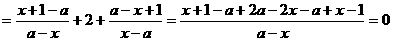 .
.
∴结论成立 ………………………………………………………………………………4’
(2)证明: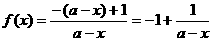
当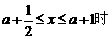 ,
,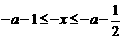 ,
,
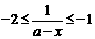 ,
,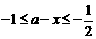 ,
,
∴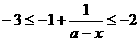 .
.
即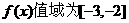 .………………………………………………………………8’
.………………………………………………………………8’
(3)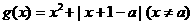
①当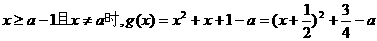 .
.
如果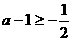 即
即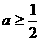 时,则函数在
时,则函数在 上单调递增,
上单调递增,
∴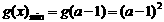 .
.
如果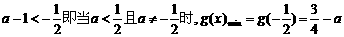 .
.
当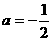 时,
时,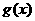 最小值不存在.……………………………………………………10’
最小值不存在.……………………………………………………10’
②当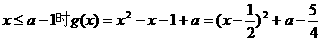 ,
,
如果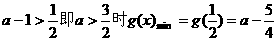 .
.
如果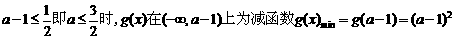 .
.
当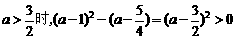 .
.
 .……………………………………………12’
.……………………………………………12’
综合得:当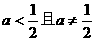 时, g(x)最小值是
时, g(x)最小值是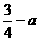 ;当
;当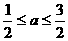 时, g(x)最小值是
时, g(x)最小值是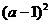 ;当
;当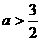 时, g(x)最小值为
时, g(x)最小值为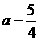 ;当
;当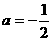 时, g(x)最小值不存在.
时, g(x)最小值不存在.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com