2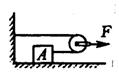．如图所示，在水平拉力F作用下，使重40N的物体A匀速移动5m，物体A受到地面的摩擦力为5N，不计滑轮、绳子的重力及摩擦，拉力F做的功　　 (　 )

A．50J　　 B．25J　　 C．100J　　 D．200J　　

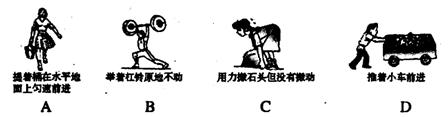
1．在图中的四种情境中，人对物体做功的是(　　 )

3．信息技术与数学学科的有机结合，使重点得以突出，难点得以突破

这节课内容的要求较高，学生由于受到年龄、思维能力以及所学知识的限制，不能很好地将知识整理、归纳，要想概括出其中的规律也是比较困难的。因此在本节课的教学中，利用电脑操作形象直观的特点及学生小组合作探索，在实验、交流、讨论、说理的过程中，使重点得以突出，难点得以突破。但这节课对电脑操作有一定要求，部分学生电脑操作能力较弱，虽然课前有过培训，但速度较慢，因此在今后教学中应不断加强学生信息技术素养的培养。

2．电脑与网络的运用，使学生学习方式多样化。

电脑给学生一个现实的实验情境，给学生一个探索的空间，使学生能够真正地的在“做”中学数学，在做的过程中，注重学生经历了知识的形成过程、注重学生的探究学习过程，在活动的过程中，体现了学生的主体作用，提高了学生的电脑操作能力。网上查询及BBS的使用，让学生能多途径吸取信息，达到自主学习，并让学生的交流方式、学习方式多样化了，使学生乐意投入到现实的、探索性的数学活动中。虽然整节课注重关注学生，师生互动较好，但个别较内向的学生在小组讨论时，没有发表自己的意见，积极性不够，因此在今后教学中更应全面关注每一个学生。

课后反思

1．激发学生兴趣，充分调动学生学习积极性。

在教学中，学生要学会把实际问题抽象成数学问题，逐渐培养他们分析问题和解决问题的能力，从而树立起数学意识。要学有价值的数学。长期以来，在部分学生的脑海里，数学始终是抽象、乏味的，对数学知识在实际生活中的应用感到茫然，而在这节课上，学生用学过的多边形的知识探索图形镶嵌的秘密，能充分感受到数学的有用性、实用性，并通过镶嵌图片的展示，让学生感受到图形的美、数学的美，从而激发学生的学习兴趣。

在活动中，由于拼装结果并不惟一，这会激发学生学习数学的兴趣，帮助他们在自主探索和合作交流的过程中，真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。

学生通过讨论，在电脑上动手操作，亲自体验数学知识的应用，并分析、归纳出一般性的结论。将知识应用于实践，又上升到理论，这样的教学使学生经历实验、观察、猜想、论证等过程，体验了发现与实践的过程，同时得出的结论记忆也会较深刻。

21.请以“踮起脚尖”为题目，写一篇不少于800字的议论文或记叙文。 (60分)