
3.偶函数
⑴偶函数: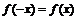 .设(
.设(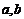 )为偶函数上一点,则(
)为偶函数上一点,则(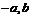 )也是图象上一点.
)也是图象上一点.
⑵偶函数的判定:两个条件同时满足
①
定义域一定要关于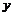 轴对称,例如:
轴对称,例如: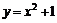 在
在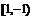 上不是偶函数.
上不是偶函数.
②
满足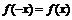 ,或
,或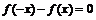 ,若
,若 时,
时,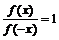 .
.
2、单调性:研究函数的单调性应结合函数单调区间,单调区间应是定义域的子集。
判断函数单调性的方法:
① 定义法(作差比较和作商比较);
② 图象法;
③ 单调性的运算性质(实质上是不等式性质);
④ 复合函数单调性判断法则;
⑤ 导数法(适用于多项式函数)
注:函数单调性是函数性质中最活跃的性质,它的运用主要体现在不等式方面,如比较大小,解抽象函数不等式等。
1、函数的单调区间可以是整个定义域,也可以是定义域的一部分. 对于具体的函数来说可能有单调区间,也可能没有单调区间,如果函数在区间(0,1)上为减函数,在区间(1,2)上为减函数,就不能说函数在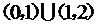 上为减函数.
上为减函数.
15、已知函数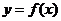 为奇函数,若
为奇函数,若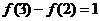 ,则
,则 1.
1.
14、设函数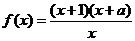 为奇函数,则
为奇函数,则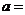 -1.
-1.
13、已知函数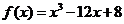 在区间
在区间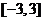 上的最大值与最小值分别为
上的最大值与最小值分别为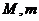 ,则
,则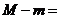 24.
24.
12、函数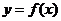 的图象与函数
的图象与函数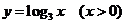 的图象关于直线
的图象关于直线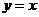 对称,则
对称,则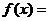 3
3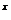 。
。
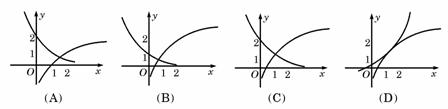
9、函数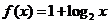 与
与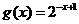 在同一直角坐标系下的图象大致是C
在同一直角坐标系下的图象大致是C
8、函数 的单调增区间为 (
的单调增区间为 ( )
)
7、已知定义域为R的函数f(x)在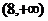 上为减函数,且函数y=f(x+8)函数为偶函数,则D
上为减函数,且函数y=f(x+8)函数为偶函数,则D
A.f(6)>f(7) B.f(6)>f(9) C.f(7)>f(9) D.f(7)>f(10)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com