
5. 如图为函数y=m+lognx的图象,其中m,n为常数,则下列结论正确的是
( )
如图为函数y=m+lognx的图象,其中m,n为常数,则下列结论正确的是
( )
?A.m<0,n>1 B.m>0,n>1
?C.m>0,0<n<1 ?D.m<0,0<n<1
答案?D?
4.(2008·杭州模拟)已知偶函数f(x)满足条件:当x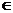 R时,恒有f(x+2)=f(x),且0≤x≤1时,有
R时,恒有f(x+2)=f(x),且0≤x≤1时,有
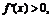 则f
则f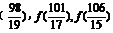 的大小关系是
( )
的大小关系是
( )
A.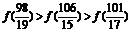 B.
B.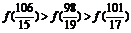
C. D.
D.
答案 B
3.(2008·湛江模拟)下列函数在其定义域内既是奇函数又是增函数的是 ( )
?A. (x∈(0,+∞))
?B.y=3x(x∈R)
(x∈(0,+∞))
?B.y=3x(x∈R)
?C. 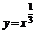 (x∈R)
?D.y=lg|x|(x≠0)
(x∈R)
?D.y=lg|x|(x≠0)
答案?C?
2.下列同时满足条件①是奇函数;②在[0,1]上是增函数;③在[0,1]上最小值为0的函数是 ( )
?A.y=x5-5x?
B.y=sinx+2x
C.y=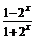 ?
D.y=
?
D.y=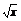 -1
-1
答案?B?
1.函数y= 的定义域是
( )
的定义域是
( )
A.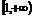 B.
B.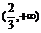 C.
C.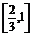 D.(
D.(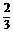 ,1]
,1]
答案 D?
12.某工厂生产某种产品,已知该产品的月生产量x(t)与1 t产品的价格p(元/t)之间的关系为:
p=24 200-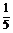 x2,且生产x t的成本为R(元),其中R=50 000+200x.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
x2,且生产x t的成本为R(元),其中R=50 000+200x.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
解 每月生产x t时的利润为
f(x)=(24 200-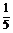 x2)x-(50 000+200x)=-
x2)x-(50 000+200x)=-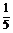 x3+24
000x-50 000 (x≥0),
x3+24
000x-50 000 (x≥0),
由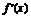 =-
=- x2+24
000=0,
x2+24
000=0,
解得x1=200,x2=-200(舍去).
因f(x)在[0,+∞)内只有一个极值点x=200且为极大值,故它就是最大值点,且最大值为
f(200)=-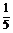 (200)3+24 000×200-50 000=3 150 000(元).
(200)3+24 000×200-50 000=3 150 000(元).
故该厂每月生产200吨产品才能使利润达到最大且最大利润为3 150 000元.
? 单元检测二
11.一位牧民计划用篱笆为他的马群围一个面积为1 600 m2的矩形牧场,由于受自然环境的影响,矩形的一边不能超过
a m,求用最少篱笆围成牧场后矩形的长与宽.
解 设一边的长为x m,0<x≤a,则宽为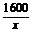 m,矩形的周长为W,
m,矩形的周长为W,
那么W=2(x+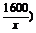 ,则W=2
,则W=2
显然当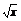 =
=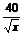 ,即x=40时,
,即x=40时,
若a≥40时,周长W最小,其最小值为160,
此时,矩形的长与宽都是40 m.
若0<a<40时,由于函数W=2(x+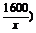 在区间(0,a]上是减函数,则当x=a时,周长W最小,其最小值为2(a+
在区间(0,a]上是减函数,则当x=a时,周长W最小,其最小值为2(a+ ,此时,矩形的长与宽分别是a m与
,此时,矩形的长与宽分别是a m与 m?.
m?.
故当a≥40时,矩形的长与宽都是40 m;
当0<a<40时,矩形的长与宽分别是a m与 m.
m.
10.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出 厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
解 (1)设每个零件的实际出厂价恰好降为51元时,一次订购量为x0个,则x0=100+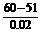 =550,
=550,
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元.
(2)当0<x≤100时,P=60;
当100<x<550时,P=60-0.02(x-100)=62- ;
;
当x≥550时,P=51,
所以P=f(x)=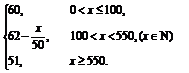
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,则
L=(P-40)x=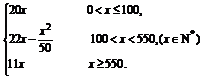
当x=500时,L=6 000;当x=1 000时,L=11 000,
因此,当销售商一次订购500个零件时,该厂获得的利润是6 000元;如果订购1 000个,利润是11 000元.
9.某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元,已知甲、乙两用户该月用水量分别为5x,3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费.
解 (1)当甲的用水量不超过4吨时,即5x≤4,
乙的用水量也不超过4吨,y=(5x+3x)×1.8=14.4x;
当甲的用水量超过4吨,乙的用水量不超过4吨时,
即3x≤4且5x>4,
y=4×1.8+3x×1.8+3×(5x-4)=20.4x-4.8.
当乙的用水量超过4吨时,
即3x>4,y=8×1.8+3(8x-8)=24x-9.6,
所以y=
(2)由于y=f(x)在各段区间上均为单调递增,
当x∈[0,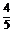 ]时,y≤f(
]时,y≤f(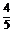 )<26.4;
)<26.4;
当x∈(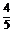 ,
,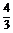 ]时,y≤f(
]时,y≤f(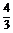 )<26.4;
)<26.4;
当x∈(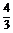 ,+∞)时,令24x-9.6=26.4,解得x=1.5,
,+∞)时,令24x-9.6=26.4,解得x=1.5,
所以甲户用水量为5x=7.5吨,
付费S1=4×1.8+3.5×3=17.70(元);
乙户用水量为3x=4.5吨,
付费S2=4×1.8+0.5×3=8.70(元).
8.某商场宣传在节假日对顾客购物实行一定的优惠,商场规定:
①如一次购物不超过200元,不予以折扣;
②如一次购物超过200元,但不超过500元,按标价予以九折优惠;
③如一次购物超过500元的,其中500元给予九折优惠,超过500元的给予八五折优惠;某人两次去购物,分别付款176元和432元,如果他只去一次购买同样的商品,则应付款 元.
答案 582.6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com