
9.(2009·菏泽模拟)函数f(x)定义在R上且f(x+3)=f(x),当 ≤x≤3时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.
≤x≤3时,f(x)=log2(ax2-2x+2).若f(35)=1,求实数a的值.
解 由题意知f(x)的周期为3,
∴f(35)=f(3×11+2)=f(2)
=log2(a·22-4+2)=1,所以a=1.
8.f(x)、g(x)都是定义在R上的奇函数,且F(x)=3f(x)+5g(x)+2,若F(a)=b,则F(-a)= .
答案 -b+4
7.已知函数f(x)=g(x)+2,x∈[-3,3],且g(x)满足g(-x)=-g(x),若f(x)的最大值、最小值分别为M、N,则M+N= .
答案 4
6.已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则在R上f(x)的表达式为 ( )
?A.-x(x-2) ?B.x(|x|-2) C.|x|(x-2) ?D.|x|(|x|-2)
答案?B?
5.设f(x)是R上的偶函数,且在(0,+∞)上是减函数,若x1<0,且x1+x2>0,则 ( )
?A.f(x1)>f(-x2) B.f(-x1)=f(-x2)
?C.f(-x1)<f(-x2) D.f(-x1)与f(-x2)大小关系不确定
答案?A?
4.已知函数y=f(x)是定义在R上的奇函数,则下列函数中是奇函数的是 ( )
①y=f(|x|);②y=f(-x);③y=x·f(x);④y=f(x)+x.
?A.①③ B.②③ C.①④ D.②④
答案?D?
3.已知函数f(x)是R上的偶函数,g(x)是R上的奇函数,且g(x)=f(x-1),若f(0)=2,则f(2 008)的值为 ( )
A.2 ?B.0 ?C.-2 D.±2
答案 A?
2.(2008·重庆理,6)若定义在R上的函数f(x)满足:对任意x1,x2∈R有f(x1+x2)=f(x1)+f(x2)+1,则下列说法一定正确的是 ( )
?A.f(x)为奇函数? B.f(x)为偶函数
C.f(x)+1为奇函数 D.f(x)+1为偶函数
答案?C?
1. f(x),g(x)是定义在R上的函数,h(x)=f(x)+g(x),则“f(x),g(x)均为偶函数”是“h(x)为偶函数”的 ( )
?A.充要条件 B.充分而不必要的条件
?C.必要而不充分的条件 ? D.既不充分也不必要的条件
答案?B?
3.设f(x)是定义在R上的偶函数,其图象关于直线x=1对称,对任意x1、x2∈[0, ]都有f(x1+x2)=f(x1)·f(x2),
]都有f(x1+x2)=f(x1)·f(x2),
且f(1)=a>0.
(1)求f( )及f(
)及f(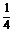 )
)
(2)证明:f(x)是周期函数;
(3)记an=f(2n+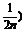 ,求an.
,求an.
(1)解 ∵对x1、x2∈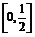 ,
,
都有f(x1+x2)=f(x1)·f(x2),
∴f(x)=f(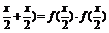 ≥0,x∈[0,1].
≥0,x∈[0,1].
∴f(1)=f(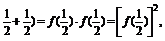
f(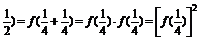 .
.
∵f(1)=a>0, ∴f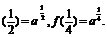
(2)证明 ∵y=f(x)的图象关于直线x=1对称,
∴f(x)=f(1+1-x),即f(x)=f(2-x),x∈R.
又由f(x)是偶函数知,f(-x)=f(x),x∈R,
∴f(-x)=f(2-x),x∈R.
将上式中-x用x代换,得f(x)=f(x+2),x∈R.
这表明f(x)是R上的周期函数,且2是它的一个周期.
(3)解 由(1)知f(x)≥0,x∈[0,1].
∵f(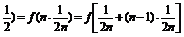 =f(
=f(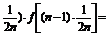 …
…
=f(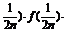 …·f(
…·f(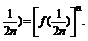 又f(
又f(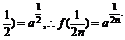
∵f(x)的一个周期是2,∴an=f(2n+ )=f(
)=f( ),∴an=a
),∴an=a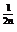 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com