
512. 以四面体各面的重心为顶点构成一个新的四面体.求这两个四面体的表面积的比.
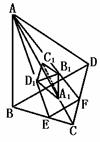
解析:因相似多面体全面积的比等于对应边的平方的比,故只须求出对应边的比.
∵B1D1=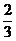 EF=
EF=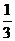 BD,
BD,
∴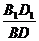 =
=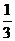 .
.
同理,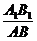 =
=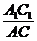 =
=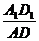 =
=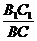 =
= =
=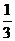 ,
,
故ABCD和A′B′C′D′是相似多面体,其表面积的比为1∶9.
511. 已知四棱锥S-ABCD的底面是边长为6的正方形,SA⊥底面ABCD,且SA=8,M是SA的中点,过M和BC作截面交SD于N.
(1)求证:截面MBCN是梯形,并求截面的面积;
(2)求截面MBCN与底面ABCD的夹角α.
解析:(1)先证MN∥BC且MN≠BC.因为BC∥AD,所以AD∥截面MBCN,从而
AD∥MN,BC∥MN.
又MN=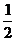 AD=
AD=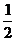 BC,所以MN≠BC.于是MN和BC平行但不相等,故MBCN是梯形.
BC,所以MN≠BC.于是MN和BC平行但不相等,故MBCN是梯形.
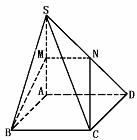
再求截面的面积:SA⊥平面ABCD.易证MN和BC都垂直于平面ABS.所以MB⊥MN,MB⊥BC,故
S截=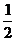 (MN+BC)·MB
(MN+BC)·MB
=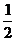 (3+6)
(3+6)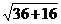 =9
=9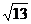 .
.
(2)首先要找到二面角的平面角.根据上面的证明,知∠MBA的是截面与底面所成二面角的平面角,即∠MBA=α.于是
tanα=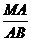 =
=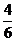 =
=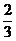
∴α=arctan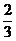
510. 棱锥被平行于底的平面分成体积相等的三部分.求这棱锥的高被分成三部分的比.
解析:设棱锥的高为h,它被截成的三部分自上而下设为h1,h2,h3,则有
(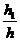 )3=
)3=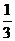 ,(
,(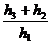 )3=2,(
)3=2,(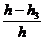 )3=
)3=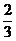 .
.
所以h1=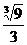 h,h2=(
h,h2=(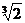 -1)h1=
-1)h1=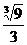 (
(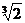 -1)h,
-1)h,
h3=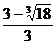 h.
h.
所以h1∶h2∶h3=1∶(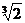 -1)∶(
-1)∶(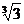 -
-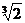 ).
).
说明 求体积之比或面积之比常用相似比.
509. 已知三棱锥S-ABC的底面面积是a,三棱锥的高是h,M、N、P、Q分别是SB、SC、AC、AB的中点,求五面体MN-PQBC的体积
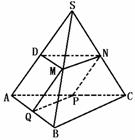
解析: 如图,过M作MD∥BA交SA于D,则D是SA的中点,连结ND,则ND∥AC
所求五面体MN-PQBC的体积等于原三棱锥的体积与五面体SA-MQPN的体积之差
而VS-ABC=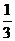 ah,
ah,
VS-DMN=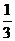 ·
·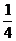 a·
a·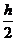 =
=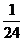 ah,
ah,
V三棱主柱DMN-APQ=S△AQP·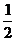 h=
h=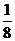 ah,
ah,
∴VMN-PQBC=VS-ABC-VSA-MQPN
=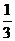 ah-(
ah-(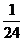 ah+
ah+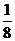 ah)
ah)
= ah
ah
508. 三棱锥A-BCD中,AC=BD,AD=BC,AB=CD,三个侧面与底面所成的二面角分别为α、β、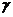 ,则cosα+cosβ+cos
,则cosα+cosβ+cos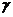 = .
= .
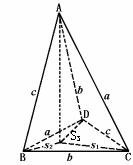
解析:如图所示,设AC=BD=a,AD=BC=b,AB=CD=c
由已知所有侧面三角形和底面三角形都是全等的三角形.
记为S,侧面在底面的射影分别为S1、S2、S3
则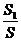 =cosα,
=cosα, 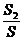 =cosβ,
=cosβ, 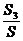 =cos
=cos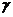
cosα+cosβ+cos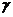 =
=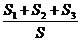 =
=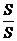 =1
=1
507. 下列命题中是真命题的是( )
A.底面是正方形的棱锥是正四棱锥
B.各条侧棱都相等的棱锥是正棱锥
C.由一个面是多边形,其余各个面是三角形所围成的几何体是棱锥
D.正四面体是正三棱锥
解析: 解此题时概念要明确,正棱锥不仅要求底面是正多边形,而且还要求其顶点在底面的射影是底面的中心,所以A、B不正确,C中的各三角形没有指明共顶点,C也不正确,D是真命题,所以选D.
506. 在空间中,
①若四点不共面,则这四点中任何三点都不共线.
②若两条直线没有公共点,则这两条直线是异面直线.
以上两个命题中,逆命题为真命题的是__________.
(把符合要求的命题序号都填上)
解析:②.①的逆命题为:空间四点中若任何三点都不共线,则这四点不共面.此命题是假命题.平行四边形的四个顶点是其反例.
②的逆命题为:若两条直线是异面直线,则这两条直线没有公共点,可知此命题为真命题.
505. 如图9-19,在棱长为a的正方体ABCD-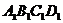 中,O是AC、BD的交点,E、F分别是AB与AD的中点.
中,O是AC、BD的交点,E、F分别是AB与AD的中点.
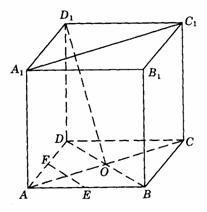
图9-19
(1)求异面直线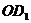 与
与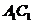 所成角的大小;
所成角的大小;
(2)求异面直线EF与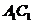 所成角的大小;
所成角的大小;
(3)求异面直线EF与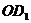 所成角的正切值;
所成角的正切值;
(4)求异面直线EF与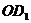 的距离.
的距离.
解析:(1)∵
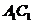 ∥AC,∴
∥AC,∴
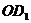 与AC所成的锐角或直角就是
与AC所成的锐角或直角就是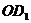 与
与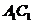 所成的角,连结
所成的角,连结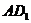 、
、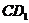 ,在△
,在△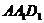 和△
和△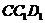 ,∵
,∵ 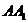 =
=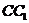 ,
,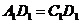 ,
,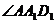
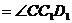
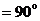 ,∴△
,∴△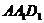 ≌△
≌△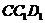 ,∴
,∴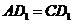 .∴△
.∴△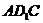 是等腰三角形.∵ O是底边AC的中点,∴
是等腰三角形.∵ O是底边AC的中点,∴
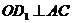 ,故
,故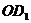 与
与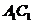 所成的角是90°.
所成的角是90°.
(2)∵ E、F分别是AB、AD中点,∴
EF∥BD,又∵
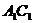 ∥AC,∴
AC与BD所成的锐角或直角就是EF与
∥AC,∴
AC与BD所成的锐角或直角就是EF与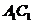 所成的角.∵ 四边形ABCD是正方形,∴
AC⊥BD,∴
EF与
所成的角.∵ 四边形ABCD是正方形,∴
AC⊥BD,∴
EF与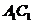 所成的角为90°
所成的角为90°
(3)∵ EF∥BD,∴
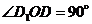 为异面直线EF与
为异面直线EF与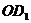 所成的角.∵ 四边形
所成的角.∵ 四边形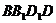 是正方形,∴
是正方形,∴ 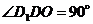 ,∴ 在Rt△
,∴ 在Rt△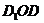 中,
中,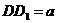 ,
,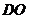 =
=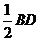 =
=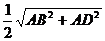
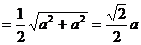 ,∴
,∴ 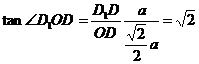 ,即EF与
,即EF与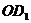 所成角的正切值为
所成角的正切值为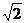 .
.
(4)∵ EF∥BD,BD⊥AC,∴
EF⊥AC,设交点为G.∵ 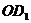 ⊥AC(由(1)
⊥AC(由(1)
知)于O,则AC是异面直线EF与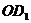 的公垂线,OG的长即为EF与
的公垂线,OG的长即为EF与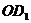 间的距离,由于G是OA中点,O是AC中点,且
间的距离,由于G是OA中点,O是AC中点,且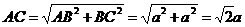 ,∴
,∴ 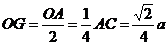 ,即EF与
,即EF与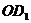 间的距离为
间的距离为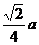 .
.
504. 如图9-18,已知P为△ABC所在平面外一点,PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点.
(1)求证:EF与PC是异面直线;
(2)EF与PC所成的角;
(3)线段EF的长.
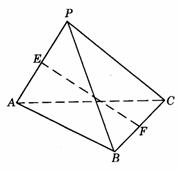
解析:(1)用反证法.假设EF与PC共面于a,则直线PE、CF共面a,则A∈a,B∈a,于是P与A、B、C共面于a,这与已知“P是平面ABC外一点”矛盾.故EF与PC是异面直线.
(2)取PB中点G,连结EG、FG,由E、F分别是线段PA、BC中点,有EG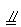
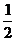 AB,GF
AB,GF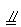
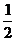 PC
∴ ∠GFE为异面直线EF与PC所成的角,∠EGF是异面直线PC与AB所成的角,∵ PC⊥AB,∴
EG ⊥GF,即∠EGF=90°.∵
PC=AB=2,∴ EG=1,GF=1,故△EFG是等腰直角三角形,∴ ∠GFE=45°,即EF与PC所成的角是45°.
PC
∴ ∠GFE为异面直线EF与PC所成的角,∠EGF是异面直线PC与AB所成的角,∵ PC⊥AB,∴
EG ⊥GF,即∠EGF=90°.∵
PC=AB=2,∴ EG=1,GF=1,故△EFG是等腰直角三角形,∴ ∠GFE=45°,即EF与PC所成的角是45°.
(3)由(2)知Rt△EGF中EG=1,GF=1,∠EGF=90°,∴
EF=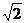
503. 借助两支铅笔,试研究以下问题:
(1)在平面内,过直线外一点有多少条直线与已知直线平行?在空间呢?
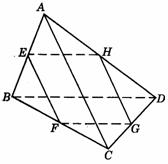
图9-17
(2)在一个平面内,过一点有多少条直线与已知直线垂直?在空间呢?
(3)在一个平面内,与该平面内的已知直线所成角为60°的直线有多少条?这些直线与已知直线的位置关系如何?在空间,与一条直线所成角为60°的直线有多少条?这些直线与已知直线的位置关系如何?
解析:(1)在一个平面内,过直线外一点有且只有一条直线与已知直线平行;在空间也如此.
(2)在一个平面内,过一点(该点可在直线上,也可在直线外)有且只有一条直线与已知直线垂线;在空间过直线上或直线外一点都有无数条直线和已知直线垂直,这无数条直线在过已知点的一个平面上(以后可知该平面与直线垂直).
(3)在一个平面内,与已知直线成60°角的直线有无数条,这无数条直线平行,且都与已知直线相交;在空间也是有无数条直线与已知直线成60°角,它们与已知直线位置关系是相交或异面.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com