
上“东海高级中学高三强化班数学周练五
一、填空题(本大题共14小题,每小题5分,共70分,把答案填写在题中的横线上)
1、集合 = ▲ .
= ▲ .
2、若幂函数 的图象不过原点,则实数
的图象不过原点,则实数 的值为 ▲ .
的值为 ▲ .
3、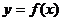 是关于
是关于 对称的奇函数,
对称的奇函数,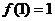 ,
, ,则
,则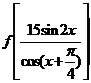 = ▲ .
= ▲ .
4、在公差不为零的等差数列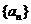 中,有
中,有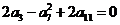 ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则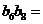 ▲
.
▲
.
5、若 则
则 = ▲ .
= ▲ .
6、若方程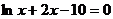 的解为
的解为 ,则大于
,则大于 的最小整数是 ▲ .
的最小整数是 ▲ .
7、若f(tanx)=cos2x,则 的值是 ▲ .
的值是 ▲ .
8、二次函数 是正整数),
是正整数),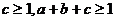 ,方程
,方程 有两个小于1的不等正根,则a的最小值为_ _▲ __.
有两个小于1的不等正根,则a的最小值为_ _▲ __.
9、在数列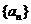 在中,
在中,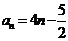 ,
, ,
,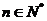 ,其中
,其中 为常数,则
为常数,则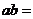 ▲ .
▲ .
10、若 为
为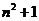
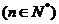 的各位数字之和,如
的各位数字之和,如 ,
,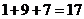 ,则
,则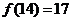 ,记
,记 ,
, ,…,
,…, ,
,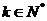 ,则
,则 ▲ .
▲ .
11、已知函数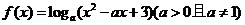 满足:对于任意实数
满足:对于任意实数 当
当 时总有
时总有 则实数a的取值范围是 ▲ .
则实数a的取值范围是 ▲ .
12、已知表中的对数值有且只有两个是错误的:
x
1.5
3
5
6
7
8
9
14
lgx
a+c
1+a-b-c
2(a+c)
3(1-a-c)
2(
1-a+2b
请你指出这两个错误 ▲ .(答案写成如lg20≠a+b-c的形式)
13、已知两个等差数列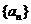 和
和 的前
的前 项和分别为A
项和分别为A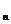 和
和 ,且
,且 ,则使得
,则使得 为整数的正整数
为整数的正整数 的个数是_ ▲
_.
的个数是_ ▲
_.
14、关于函数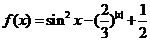 有下列四个个结论:①
有下列四个个结论:①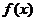 是奇函数.②当
是奇函数.②当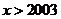 时,
时,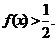 ③
③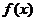 的最大值是
的最大值是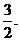 ④
④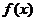 的最小值是
的最小值是 其中正确结论的序号是 ▲ .
其中正确结论的序号是 ▲ .
二、解答题(本大题共6小题,共90分,解答应写出文字说明,证明过程或演算步骤)
15(14分).集合A={1,3,a},B={1,a2},问是否存在这样的实数a,使得B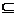 A,
A,
且A∩B={1,a}?若存在,求出实数a的值;若不存在,说明理由.
16(14分)、在 中,
中, 、
、 、
、 分别是三内角A、B、C的对应的三边,已知
分别是三内角A、B、C的对应的三边,已知 。
。
(Ⅰ)求角A的大小:
(Ⅱ)若 ,判断
,判断 的形状。
的形状。
17(14分)、已知数列{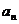 }的前n项和为Sn,若
}的前n项和为Sn,若 ,问是否存在
,问是否存在 ,使得对于一切
,使得对于一切
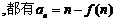 成立,请说明理由.
成立,请说明理由.
|