1、下列结论对否：

  （   ）                 （   ）

           （   ）          （   ）

         （   ）                 （   ）

2、成立的充要条件为              

3、用“＞”“＜”“＝”填空：

(1)a<b<c<0则ac    bc ；    ；     ；

(2) 0<a<b<c<1，则a^c   b^c ；a^b    a^c；log_ca    log_cb；algc    blgc；arcsina    arcsinb.

1、比较下面各小题中a与b的大小：

(1)a=m³－m²n－3mn² 与 b=2m²n－6mn²＋n³            (2)a=3x²－x＋1与b=2x²＋x－1

(3) .

2、a＞0，a≠1，t＞0，比较m=与n=的大小.

3、，1≤≤2，13≤≤20，求的取值范围.

1、若，则下列不等式成立的是………………………………………………………………… （   ）

(A)             (B)     (C)          (D)

2、设，那么下列不等式成立的是……………………………………………………… （   ）

(A)  (B)   (C)   (D) 以上都不对

3、已知，则下列不等式能成立的是 …………………………………………………………（   ）

(A)              (B)             (C)                (D)

4、已知，则下列不等式成立的是 ……………………………………………………（   ）

(A)         (B)          (C)            (D)

5、若，则下列不等关系中不能成立的是 …………………………………………………… (   )

(A)             (B)            (C)                (D)

1、不等式的基本性质是解不等式与证明不等式的理论依据，必须透彻理解，特别要注意同向不等式可相加，也可相乘，但相乘时，两个不等式都需大于零.

2、处理分式不等式时不要随便将不等式两边乘以含有字母的分式，如果需要去分母，一定要考虑所乘的代数式的正负.

3、作差法是证明不等式的最基本也是很重要的方法，应引起高度注意.

五、能力测试：                           姓名              得分          

1、下列命题中正确的是……………………………………………………………………………… (    )

(A)  (B)   (C)    (D)

2、设 ，则有 …………………………………………………………………………………（    ）

(A)          (B)       (C)             (D)

3、若,则有…………………………………………………………………… (     )

(A)          (B)            (C)             (D)以上皆错

4、若,则 ………………………………………………………………………………(     )

(A)          (B)              (C)                (D)c、d大小不确定

5、以下命题：⑴a>b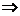|a|>b    ⑵a>b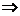a²>b²    ⑶|a|>b  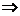a>b    ⑷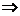a>|b|  a>b

正确的个数有………………………………………………………………………………………（    ）

(A) 1个            (B) 2个              (C)  3个              (D)4个

6、已知a＞,比较与的大小.

7、比较下列各数的大小：

(1)    （提示：分a＞1，a＜1讨论）

(2)与 （提示：分子有理化后再比较）

8、如果二次函数的图象过原点，并且1≤≤2,3≤≤4,求的取值范围.

不等式的解法――分式与高次

〖考纲要求〗在熟练掌握一元一次与一元二次不等式的解法的基础上初步分式与高次不等式的解法.

〖复习建议〗分式与高次不等式的一般解法：序轴标根法，能注意到其中的一些特殊点与解集的关系，能注意到区间端点与解集的关系.

1、下列不等式与 同解的是……………………………………………………………（    ）

(A)                             (B)   

(C)                          (D)

2、不等式(x－2)²?(x－1)>0的解集为                        .

3、不等式(x＋1) ?(x－1)²≤0的解集为                      .

4、不等式的解集为                    .

1、解不等式：(x－1)?(x－2)?(x－3)?(x－4)>120

2、解不等式：

3、解不等式：

4、若不等式对一切x恒成立,求实数m的范围

  5、求适合不等式的整数x的值.

  6、解关于x的不等式

1、不等式的解集为……………………………………………………………………（    ）

(A){x|≤x≤2}                          (B) {x|≤x<2}    

(C) {x|x>2或者x≤}                     (D){x|x＜2

2、不等式的解集为                     .

3、如果不等式的解集为（，1），则=          .

分式与高次不等式的解题基础是一元二次不等式的解法，常用方法是序轴标根法，但是要注意标根时的起点位置.

五、能力测试：

1、与不等式同解的不等式是……………………………………………………………（    ）

  (A)(x－3)(2－x)≥0     (B)lg(x－2)≤0       (C)        (D)(x－3)(2－x)>0

2、如果x₁<x₂<…<x_n，n≥2,并且{x|(x－x₁)(x－x₂)…(x－x_n)>0}{x|x²－(x₁＋x₂)x＋x₁x₂<0}，那么自然数n…………………………………………………………………………………………………（    ）

(A)等于2                                 (B)是大于2的奇数

(C) 是大于2的偶数                        (D)是大于1的任意自然数

3、不等式(x－1)(x＋2)(3－x)>0的解集为                 .

4、不等式的解集为               .

5、a>0,b>0，那么不等式的解集为                   .

6、已知不等式的解集为{x|x<1或x>2}，那么a=          .

7、解不等式：（提示：）

8、不等式对一切x都成立，求n的值.

9、解关于x的不等式

不等式的解法――指数 对数（无理不等式）

〖考纲要求〗新的考纲虽然没有明确要求掌握简单的指数、对数无理不等式的解法，但是却要求掌握函数的单调性，会利用函数单调性比较大小，而这也正是我们这一讲的出发点..

〖复习建议〗1、掌握解指数、对数不等式的方法，一般来说，与解指数、对数方程的方法类似.即：

(1)同底法：能化为同底数先化为同底，再根据指数、对数的单调性转化为代数不等式，底是参数时要注意对其进行讨论.并注意到对数真数大于零的限制条件.

(2)转化法：多用于指数不等式，通过两边取对数转化为对数不等式（注意转化的等价性）.

(3)换元法：多用于不等式两边是和的形式，或取对数后再换元，并注意所换“元”的范围.

          2、掌握基本无理不等式的转化方法.

1、当等价的不等式是 …………………………………（   ）

（A）  （B） （C） （D）以上都不对

2、当等价的不等式是 …………………………………………………（   ）

（A）（B）（C）  （D）

3、不等式的解集为……………………………………………………………（    ）

（A）{x|x<2}         （B）{x|0<x<2}       （C）{x|1<x<2}      （D）{x|x>2}

4、不等式(x－1)的解为……………………………………………………………（    ）

(A)x≥1　          (B)x>1               (C) x≥1或者x=－2  (D) x≥－2且x≠1

5、不等式 的解集为            ；

  1、解不等式

2、解不等式 .

3、如果x=3是不等式：的一个解，解此关于x的不等式.

4、解关于x的不等式：

*5、解不等式：

1、不等式 的解集为                ；

2、不等式的解集为             ；

3、不等式的解集是 ……………………………………………………………（   ）

（A）       （B）       （C）       （D）

掌握指数、对数、无理不等式的常规解法―取对数法、换底法、换元法、利用函数单调性，将它们转化为代数不等式.在进行转化时，应充分注意函数定义域，保证同解变形.在转化为求不等式组的解时，应注意区别“且”、“或”，涉及到最后几个不等式的解集是“交”，还是“并”.

五、能力测试：

1、与不等式同解的不等式是 …………………………………………………………（   ）

（A）   （B）    （C）      （D）

2、不等式的解为 ……………………………………………………………………（   ）

（A）x>11           （B）x<－9         （C）x<－9或x>11   （D）－9<x<11

3、设c<0，下列不等式成立的是 ……………………………………………………………………（   ）

（A）        （B）     （C）       （D）

4、不等式的解集为……………………………………………………………………（    ）

（A）{x|x≤1}        （B）{x|＜x≤1   （C）{x|＜x＜1  （D）R

5、不等式 的解集为 ……………………………………………………………………（   ）

（A）    （B） (C)           （D）

6、 的同集不等式为 …………………………………………………（    ）

(A) (B)     (C) (D）

7、                   

8、不等式lgx＋lg(x－3)<1的解集为              .

9、解关于x的不等式：

*10、解不等式

不等式的证明―比较法

〖考纲要求〗掌握不等式的性质及其证明，能正确使用这些性质解决一些简单问题.

〖复习建议〗掌握求差法与求商法比较两个数的大小。

〖双基回顾〗

1、求差法：a＞b a－b＞0          2、求商法：a＞b＞0

3、用到的一些特殊结论：同向不等式可以相加（正数可以相乘）；异向不等式可以相减；

1、已知下列不等式:

       其中正确的个数为 ……………………………………………………………………………………(    )

(A)0                 (B)1                (C) 2                 (D) 3

2、1＞a＞b＞0，那么…………………………………………………………………………………（    ）

(A)a＞＞＞b                    (B) b＞＞＞a

(C) a＞＞b＞                    (D) ＞＞a＞b

3、如果－＜b＜a＜，则b－a的取值范围是……………………………………………………（    ）

(A)－＜b－a＜0     (B) －＜b－a＜   (C) －＜b－a＜0    (D) －＜b－a＜

4、已知      1.（填“>”或者“<”）

1、求证：若a、b>0,n>1,

2、a、b、c、d、m、n全是正数，比较p=q=的大小.

3、比较的大小

4、a∈R，函数

(1)判断此函数的单调性。

(2)F(n)=,当函数为奇函数时，比较的大小.

1、a＞b与同时成立，那么有………………………………………………………………（    ）

(A) a＞b＞0          (B) a＞0＞b         (C) ＞0          (D)

2、

    比较法是证明不等式最常用最基本的方法.当欲证的不等式两端是多项式或分式时，常用差值比较法。当欲证的不等式两端是乘积的形式或幂指不等式时常用商值比较法，即欲证

五、能力测试：                           姓名              得分          

1、不等式：⑴x³＋3>2x；⑵a⁵＋b⁵<a³b²＋a²b³；⑶a²＋b²≥2(a＋b－1)；⑷恒成立的有(    )

(A)⑴、⑵           (B) ⑴、⑶          (C) ⑶、⑷         (D) ⑴、⑵、⑶、⑷

2、 对都成立的不等式是…………………………………………………………………… (    )

(A) (B)      (C)       (D)

3、0＜a＜1，F=，G=，H=，那么F、G、H中最小的是…………………………（    ）

(A)F                (B) G               (C) H              (D) 不能确定

4、a>b>0，则下列不等式恒成立的是………………………………………………………………（    ）

(A)      (B)      (C)   (D) a^a>b^b

5、x>100，那么lg²x,lgx²,lglgx从大到小的顺序为                   .

6、a＞0，b＞0，a＋b=1，比较M=x²＋y²与N=(ax＋by)²＋(bx＋ay)²的大小.

7、比较大小

8、求证：

9、比较A=a⁶＋a⁴＋a²＋1与B=a⁵＋a³＋a的大小.（提示：分a＞1，a=1，a＜1讨论）

证明：a＞1时，A－B=a⁶＋a⁴＋a²＋1－（a⁵＋a³＋a）=(a⁶－a⁵)＋(a⁴－a³)＋(a²－a)＋1

不等式证明的其它方法

〖考纲要求〗掌握用“分析法”证明不等式；理解反证法、换元法、判别式法、放缩法证明不等式的步骤及应用范围.

〖复习建议〗搞清分析法证题的理论依据，掌握分析法的证题格式和要求。搞清各种证明方法的理论依据和具体证明方法和步骤。

说明：数学归纳法法证明不等式将在数学归纳法中专门研究.

〖双基回顾〗

1、“分析法”证题的理论依据：寻找结论成立的充分条件或者是充要条件.

2、“分析法”证题是一个非常好的方法，但是书写不是太方便，所以我们可以利用分析法寻找证题的途径，然后用“综合法”进行表达.

1、推理：如果a≠b，要证a²＋b²<1＋a²b²，由于2ab<a²＋b²，只要证：2ab<a²＋b²    正确吗？

2、推理：要证|a＋b|≤|a|＋|b|，只要证|a＋b|²≤(|a|＋|b|)²                            正确吗？

3、推理：要证a<b，只要证a²<b²                                                 对吗？

4、a、b、c∈R，a＞b是ac²＞bc²成立的…………………………………………………………（    ）

(A)充分条件      (B)必要条件      (C)充要条件      (D)既不充分又不必要条件

1、x＞0，y＞0，求证：

2、a＞b＞0，2c＞a＋b，求证：

3、函数，求证：

4、（三角换元法）

5、求证： （判别式法）

6、若a,b,c都是小于1的正数，求证：（反证法）

7、求证：（放缩法）

1、a＞b＞0，求证：

2、A、B、C是ㄓABC的内角，求证：x²＋y²＋z²≥2yzcosA＋2zxcosB＋2xycosC.（判别式法）

1、“分析法”证明不等式就是“执果索因”，从所证的不等式出发，不断利用充分条件或者充要条件替换前面的不等式，直至找到显然成立的不等式，书写方法习惯上用“”来表达.

2、凡是“至少”、“唯一”或含有否定词的命题适宜用反证法.

3、换元法（主要指三角代换法）多用于条件不等式的证明，此法若运用恰当，可沟通三角与代数的联系，将复杂的代数问题转化成简单的三角问题.

4、含有两上字母的不等式，若可化成一边为零，而另一边是关于某字母的二次式时，这时可考虑判别式法，并注意根的取值范围和题目的限制条件.

5、有些不等式若恰当地运用放缩法可以很快得证，放缩时要看准目标，做到有的放矢，注意放缩适度.

五、能力测试：                           姓名              得分          

1、如果P=，Q=1+，R=，那么有………………………………………………（    ）

(A)P＞Q＞R         (B)R＞P＞Q          (C) Q＞R＞P        (D)R＞Q＞P

2、a＞b＞0，那么下列不等式中恒成立的是………………………………………………………（    ）

(A)     (B)      (C)      (D)

3、四个命题：⑴a²＜b²|a|＜|b|  ⑵ a²＜b²a＋b与a－b符号相反  ⑶a²＜b²|a|＋|b|与|a|－|b|符号相反  ⑷a²＜b²|a|²＜|b|²符号相反  其中是真命题的有……………………………（    ）

(A) 4个             (B)3个               (C) 2个             (D)1个

4、x、y∈R，|x|＜1，|y|＜1是0＜xy＜1的………………………………………………………（    ）

(A) 充分条件        (B)必要条件           (C) 充要条件       (D)既不充分也不必要条件

5、a、b、c∈R^-，a≠b，求证：

6、a＞b＞c，求证：

（提示：换元法，令a－b=m∈R^＋，b－c=n∈R^＋）

7、求证：

8、证明不等式：（提示：使用放缩法）

9、x＞0，y＞0并且x+y＞2，求证中至少有一个小于2（提示：反证法）

不等式的应用

〖考纲要求〗

1、熟练运用不等式的知识综合解决函数、方程等中的有关问题.

2、在掌握一次函数单调性、二次函数的最值以及在定区间上的最值问题，学会变量的转换，掌握：恒正、恒负、解集为R、解集为空集的实际含义并且会转化

3、掌握 “两个正数的算术平均数不小于他们的几何平均数”，并能运用此定理解决一些问题.

〖复习建议〗重要不等式的功能在于和积互化，要注意三个条件：一正、二定、三相等的检验。在运用过程中，要注意创造特殊的环境：

1、下列函数中，最小值为4的是………………………………………………………………… (    )

(A)                           (B)

(C)                        (D)

2.当x               时，等式成立；

当x              时，等式成立.

1、若的最值.

2、的最小值.

3、时恒正，求x的取值范围（关于a的一次函数）.

4、函数=x²＋ax＋3，当x∈[－2，2]时，恒有≥a，求a的最小值.

   5、已知函数，x∈[a，b]，如果对任意的x∈[a，b]，都有，则就称可以被函数y=“替代”.试判断：函数 ，x∈[4，16]是否可以被函数=，x∈[4，16]替代，并且说明理由！

*6、设函数是定义在R上的单调函数并且满足：，

⑴求证：为奇函数  ⑵为减函数 

⑶如果+>0恒成立，求实数k的取值范围.

1、有意义，则实数a的取值范围是                   .

2、，则实数a的取值范围是               .

1、若x+2y=4,且x>0,y>0,则 lgx+lgy的最大值为 ……………………………………………………（   ）

（A）2              （B）2lg2              （C）lg2             （D）

2、设a,b为实数，且a+b=3,则2^a+2^b的最小值是 ……………………………………………………（   ）

（A）6              （B）             （C）           （D）8

3、函数图象上最低点的坐标为………………………………………………（   ）

（A）（0，5）         (B) （3，4）           (C) （3，2）          (D) （8，）

4、x、y∈R⁺，那么不等式恒成立的最小正数a=        .

5、(1)若的最大值是          ；(2)函数tgx+ctgx的值域是                    ；

6.现有含盐7%的食盐水200克，生产上需要含盐在5%以上，6%以下的食盐水，设需要加入含盐

4%的食盐水x克，则x的范围是           .

7、函数y=x²＋ax＋3的图象恒在函数y=2ax－5的上方，求实数a的取值范围.

8、定义在上的函数y=单调递减，是否存在实数k，使： 对一切实数恒成立？存在请求出，不存在请说明理由！

*9、对满足：|p|＜2的一切p，不等式＋p＋1＞2＋p恒成立，求实数x的取

值范围（提示：可以理解为关于p的一次函数）.

不等式的应用2

〖考纲要求〗

能运用不等式的知识解决实际问题.

〖复习建议〗

    能从实际问题中抽象出数学模型，寻找出该数学模型中已知量与未知量，建立数学关系式，并用适当的方法解决问题。

1、已知三角形的三边长分别为15，19，23厘米，把它的三条边长分别缩短x厘米，使它只能构成钝角三角形，求x的取值范围.

2、从边长为2a的正方形铁皮的四角各截去一小块边长为x的正方形，再将

四边向上折起，做成一个无盖的方铁盒，问x取何值时，盒的容积最大？

最大的容积为多少？

3、某杂志若以每本2元的价格出售，可以发行10万本，若每本价格提高0.2元，发行量就少5000

本，要使销售总收入不低于22.4万元，则该杂志的定价最高和最低各为多少？

4、在某种商品生产过程中，每日次品数y是每日产量x的函数：，该产品每售出一件正品获得利润A元，每生产一件次品就损失元，为了获得最大利润，日产量应该是多少？

5、（12分）在某海滨城市附近海面有一台风，根据监测，当前台风中心位于城市O（如图）的东偏南（）方向300km的海面P处，并且以20km/h的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并且以10km/h的速度不断增大，问几个小时后，该城市开始受到台风的侵袭？

*6、甲、乙两地相距240千米,汽车从甲地匀速行驶到乙地,速度不得超过60千米/时.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为b；固定部分为a元.

⑴全程运输成本把y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;

⑵为了使全程运输成本最小,汽车应以多大速度行驶?

1、等边圆锥母线长为8，其的内接圆柱的高为x，当内接圆柱侧面积最大时，x的值为………（    ）

（A）3              （B）2         （C）           （D）4

次

案

第一次提价

第二次提价

甲

p%

q%

乙

q%

p%

丙

2、某商店计划两次提价，有甲、乙、丙三种方案，(如右表，其

中p>q>0.)经两次提价后，则     种方案的提价幅度最大！

3、某工厂生产一种文具所需支付的费用有三种：

⑴不论生产不生产，都需支付职工工资等固定开支1.25万元；

⑵生产x件产品，所需各种原材料费用，平均每件36元；

⑶由于能源供应的特殊政策，经测算，生产x件产品的能源

费为每件0.05x元.

   问这种文具平均每件生产成本最低是多少元？

4、某工厂有旧墙一面14米，现在准备利用这面旧建造平面图形为矩形、面积为126平方米的厂房，条件是⑴建1米新墙的费用为100元；⑵修1米旧墙的费用为25元；⑶拆1米旧墙，用所得的材料建1米新墙的费用为50元，现在有两种方案：

第一种：利用旧墙的一面长为x米（0<x<14米）；

第二种：利用旧墙的一面长为x米（x≥14米）.    问：那一种方案好？最少费用是多少？

5、某轮船公司争取到一个相距1000海里的甲、乙两地的航运权，已知轮船限载400人，轮船每小时的燃料费用和轮船的速度的立方成正比，轮船的最大时速为25海里/小时，当航速为10海里/小时时，它的燃料费用为30元/小时，其余费用（与速度无关）都是480元/小时，如果公司打算从每个顾客身上获得平均利润a元，在轮船满载航行时，你能为该公司设计一种比较合理的船票价格吗？为什么！

*6、某保健中心用60万元买进一台仪器，该仪器第一年的保养、维修费为1.2万元，以后每年保养、

维修费都比上一年增加2千元，第一年管理人员工资费用2万元，以后每年比上一年增加5%，

据调查平均每年有1000人次使用次仪器，如果计划10年收回投资（含购买、保养、维修、工资等），问每人检查一次应该收费不少于多少元？

  *7、设计一宣传画，要求画面面积4840cm²，画面的宽与高的比为（<1）,画面的上下各留8cm空白,左右各留5cm空白,怎样确定画面宽与高的尺寸,才能使宣传画所有的纸张面积最小?如果要求∈[],那么为何值时, 才能使宣传画所有的纸张面积最小?(2001广东题)

高三数学总复习测试――不等式

                   姓名              得分       

1、四个命题：⑴a>b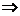|a|>b；⑵a>b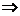a²>b²；⑶|a|>b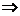a>b；⑷a>|b|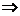a>b  正确的共有…（    ）

  (A)1个                (B)2个             (C) 3个               (D)4个

2、如果1<a<b,a+b=1,那么四个数：b，2ab，，最大的是…………………………（    ）

  (A)b                  (B)2ab              (C)              (D)  

3、1＞x＞0，下列三个数：a=，b=1＋x，c=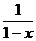，则其中最大的一个是……………………（    ）

(A)a                  (B) b                (C) c                 (D) 不能确定

4、不等式组有解，则实数a的取值范围是……………………………………………（    ）

(A)(－1,3)                                 (B) (－3,1)  

(C) (－∞,－1)∪(3,＋∞)                     (D) (－∞,－3)∪(1,＋∞)

5、x是实数，则下列不等式恒成立的是……………………………………………………………（    ）

(A)        (B)        (C)  (D)  

6、如果实数x、y、m、n满足x²＋y²=a，m²＋n²=b，则mx＋ny的最大值为……………………（    ）

  (A)              (B)            (C)              (D)

7、如果a，b＞0，并且4x+y=a，如果xy的最大值为16，那么常数a=………………………………（    ）

(A)8                  (B) 64               (C) 32                 (D) 16

8、下列函数中，最小值为2的是……………………………………………………………………（    ）

(A)                              (B)   

(C)                        (D)

9、不等式的解集为…………………………………………………………………（    ）

(A)(0,1)             (B)(0,＋∞)             (C) (1,＋∞)            (D) (－∞，1) 

10、如果的值恒为正数，那么a的取值范围是………………………………………（    ）

(A)a＞            (B)          (C)a＞1               (D) a＞1或

11、如果不等式：|x－2|+|x－5|≥a的解集为R，那么实数a的取值范围是………………………（    ）

(A)           (B)              (C)             (D)

12、如果方程：x²－x－(m＋1)=0在[－1，1]上有解，则m的范围是…………………………………（    ）

(A)            (B)         (C)             (D)

13、不等式：(a²－1)x²－(a－1)x－1<0对任意实数都成立，那么实数a的取值范围是              .

14、不等式组的解集为                       .

15、如果关于x的不等式：x²－ax－4<0的解集是(－1,m)，那么a=       ；m=        .

16、设a、b、x都是正数，且a、b是常数，则函数的最小值为             .

17、解不等式：

18、一批货物随17列货车从A地以vkm/h的速度匀速直达B地，已知两地铁路线长400km，为了安全，两货车距离不得小于km，求这批货物全部抵达B地所需要的最少时间！

19、已知奇函数在定义域（－1，1）上单调递减，并且满足：，

求实数a的取值范围.

20、某小区要建一个面积为a平方米的矩形绿地，四周有小路，绿地长边外路宽5米，短边外小路宽8米，绿地边长至多长28米，最小长20米，对于给定的a（300≤a≤700），怎样设计绿地的长与宽，使绿地和小路所占的总面积最小！

21、已知曲线C₁的方程为xy=－1，曲线C₁关于点M（－，）的对称曲线为C₂.

⑴求曲线C₂的表达式并求函数的单调区间；

⑵如果，求证：

22、已知二次函数=ax²＋bx＋c（a、b、c是实数）同时满足下列条件：⑴；⑵对任意实数x，都有－x≥0；⑶当x∈（0，2）时，有.

⑴求；

⑵求a、b、c；

⑶当x∈[－1，1]时，=－mx（m是实数）是单调函数，求实数m的取值范围.