2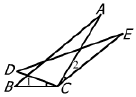．如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是(　　 )

(A) SAS　　 (B) ASA　　 (C) AAS　　 (D) SSS

1．ax²+bx+c=0，是一元二次方程的条件是(　 ).

(A)a,b,c为任意实数　 (B)a与b不同时为零

　(C)a取不为零的实数　 (D)b与c不同时为零　 27.2.6

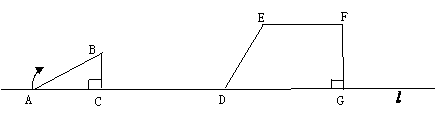
28.(14分)已知：如图，在直线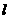上摆放有△ABC和直角梯形DEFG，且CD＝6㎝；在△ABC中：∠ACB＝90^O，∠A＝30⁰，AB＝4㎝；在直角梯形DEFG中：EF//DG，∠DGF＝90^O ,DG＝6㎝，DE＝4㎝，∠EDG＝60⁰。解答下列问题：

(1)旋转：将△ABC绕点C顺时针方向旋转90⁰，请你在图中作出旋转后的对应图形△A₁B₁C，并求出AB₁的长度；

(2)翻折：将△A₁B₁C沿过点B₁且与直线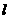垂直的直线翻折，得到翻折后的对应图形△A₂B₁C₁，试判定四边形A₂B₁DE的形状？并说明理由；

(3)平移：将△A₂B₁C₁沿直线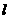向右平移至△A₃B₂C₂，若设平移的距离为x，△A₃B₂C₂与直角梯形重叠部分的面积为y，当y等于△ABC面积的一半时，x的值是多少？

友情提示：请同学做完试卷后， 再仔细检查一下，也许你会做得更好，祝你成功！

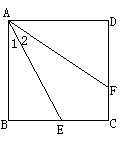
27.(10分)(1)已知：如图，在正方形ABCD中，E是BC的中点，F为DC上一点，且∠1=∠2，求证：AF=BC+FC；

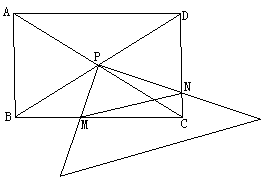
(2) 已知：如图，把三角尺的直角顶点落在矩形ABCD的对角线交点P处，若旋转三角尺时，它的两条直角边与矩形的两边BC、CD分别相交于M、N，试证：MN²=BM²+DN²。

26.(10分)如图，(1)图中将两个等宽矩形重叠一起，则重叠四边形ABCD是什么特殊四边形？请说明理由。(2)若(1)中是两个全等的矩形，矩形的长为8cm，宽为4cm，重叠一起时不完全重合，试求重叠四边形ABCD的最小面积和最大面积，并请对面积最大时的情况画出示意图。

25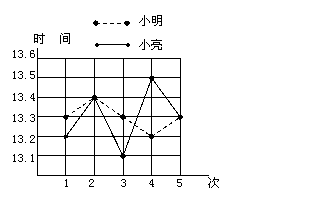．(9分)为了让广大青少年学生走向操场，走进自然，走到阳光下，积极参加体育锻炼。我国启动了“全国亿万学生阳光体育运动”。短跑运动，可以锻炼人的灵活性，增强人的爆发力，因此小明和小亮在课外活动中，报名参加了短跑训练小组。在近几次百米训练中，所测成绩如图所示，请根据图中所示解答以下问题。

(1)请根据图中信息，补齐下面的表格；

(2)分别计算他们的平均数、极差和方差填入下表格，若你是他们的教练，将小明与小亮的成绩比较后，你将分别给予他们怎样的建议？

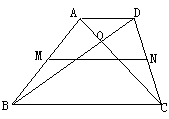
24．(8分)如图在梯形ABCD中，两对角线AC、BD互相垂直于O点，且AC=6、BD=8，试求梯形ABCD的中位线MN及高h的长？

23．(6分)(1)如图1，点O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角OAB和等边三角形OCD，连结AC和BD，相交于点E，连结BC.

求：∠AEB的大小；

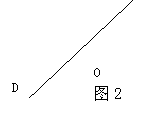
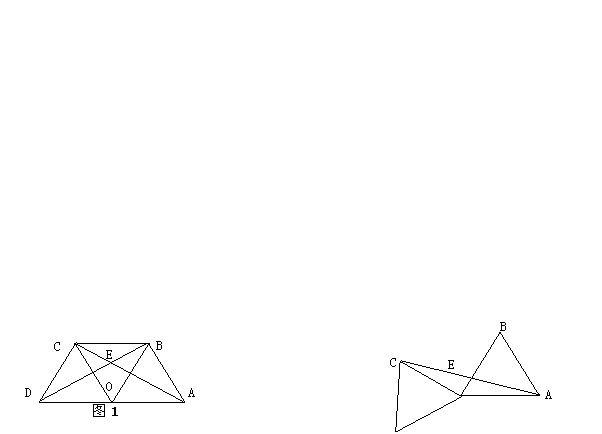
(2)如图2，△OAB固定不动，保持△OCD的形状和大小不变，将△OCD绕着点O旋转(△OAB和△OCD不能重叠)，求：∠AEB的大小.

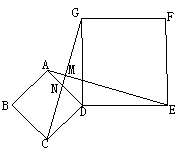
22.(6分)如图，四边形ABCD、DEFG都是正方形，连接AE、CG，AE与CG相交于点M，CG与AD相交于点N。试判断AE与CG之间的关系？并说明理由。

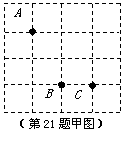
21.(6分)如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边(包括顶点)上，且四边形的顶点在方格的顶点上．

(1)在图甲中作出的四边形是中心对称图形但不是轴对称图形；

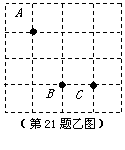
(2)在图乙中作出的四边形是轴对称图形但不是中心对称图形；

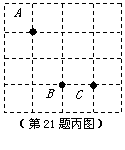
(3)在图丙中作出的四边形既是轴对称图形又是中心对称图形．