
19、(广东省北江中学2009届高三上学期12月月考)旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(Ⅰ)求3个旅游团选择3条不同的线路的概率;
(Ⅱ)求选择甲线路旅游团数的分布列和期望.
解:(1)3个旅游团选择3条不同线路的概率为:P1=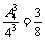 ……4分
……4分
(2)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3………………5分
P(ξ=0)=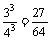 P(ξ=1)=
P(ξ=1)=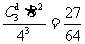
P(ξ=2)= 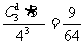 P(ξ=3)=
P(ξ=3)= 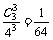 ………………9分
………………9分
∴ξ的分布列为:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
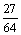 |
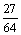 |
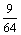 |
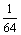
|
………………10分
∴期望Eξ=0×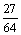 +1×
+1×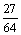 +2×
+2×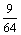 +3×
+3×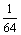 =
=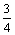 ………………12分
………………12分
18、(江苏省常州市2008-2009高三第一学期期中统一测试数学试题)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数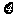 的分布列和数学期望.
的分布列和数学期望.
解:(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知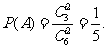 4′
4′
(2)ξ可取1,2,3,4.
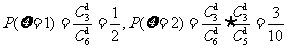 ,
,
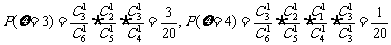 ; 8′
; 8′
故ξ的分布列为
|
ξ |
1 |
2 |
3 |
4 |
|
P |
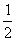 |
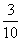 |
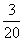 |
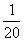 |

答:ξ的数学期望为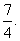 10′
10′
17、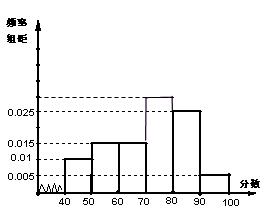 (江苏省常州市2008-2009高三第一学期期中统一测试数学试题)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(是不小于40不大于100的整数)分成六段
(江苏省常州市2008-2009高三第一学期期中统一测试数学试题)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(是不小于40不大于100的整数)分成六段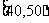 ,
,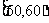 …
…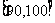 后画出如下部分
后画出如下部分
(1)求第四小组的频率,并补全这个频率分布直方图.
(2) 观察频率分布直方图图形的信息,估计这次考试的及格率(60分及以上为及格)和平均分.
解:(1)因为各组的频率和等于1,故第四组的频率:
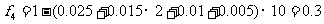 3′
3′
直方图如右所示 6′
(2)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为
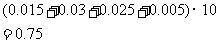
所以,抽样学生成绩的合格率是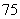 %..
9 ′
%..
9 ′
利用组中值估算抽样学生的平均分
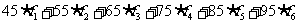
=
=71
估计这次考试的平均分是71分 12′
16、(四川省成都市高中数学2009级九校联考)在一次篮球练习课中,规定每人投篮5次,若投中2次就称为“通过”若投中3次就称为“优秀”并停止投篮。已知甲每次投篮投中概率是。
(1)求甲恰好投篮3次就“通过”的概率;
(2)设甲投中篮的次数为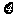 ,求随机变量
,求随机变量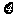 的分布列及期望
的分布列及期望 。
。
解:①前2次中恰有一次投中且第3次也投中,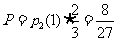 …………5分
…………5分
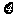 |
0 |
1 |
2 |
3 |
|
p |
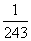 |
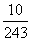 |
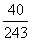 |
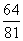 |
②
……………………………………5分
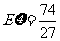 …………………………2分
…………………………2分
15、(四川省成都市高中数学2009级九校联考)某单位组织4个部门的职工旅游,规定每个部门只能在峨眉山、泰山、华山3个景区中任选一个,假设各部门选择每个景区是等可能的.
(Ⅰ)求3个景区都有部门选择的概率;
(Ⅱ)求恰有2个景区有部门选择的概率.
解:某单位的4个部门选择3个景区可能出现的结果数为34.由于是任意选择,这些结果出现的可能性都相等.
(I)3个景区都有部门选择可能出现的结果数为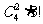 (从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有
(从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有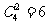 种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为
种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为
P(A1)=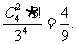 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
(II)解法一:分别记“恰有2个景区有部门选择”和“4个部门都选择同一个景区”为事件A2和A3,则事件A3的概率为P(A3)=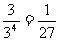 ,事件A2的概率为
,事件A2的概率为
P(A2)=1-P(A1)-P(A3)=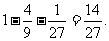 。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。6分
14、(2009届福建省福鼎一中高三理科数学强化训练综合卷一)下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为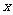 ,数学成绩为
,数学成绩为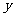 。设
。设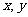 为随机变量(注:没有相同姓名的学生)
为随机变量(注:没有相同姓名的学生)
  |
数学 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英语 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
 |
6 |
0 |
 |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
(1)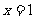 的概率为多少?
的概率为多少?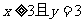 的概率为多少?
的概率为多少?
(2) (理)  等于多少?若
等于多少?若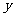 的期望为
的期望为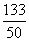 ,试确定
,试确定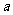 ,
, 的值 .
的值 .
解:(1)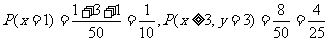 ;6分
(2)(理)
;6分
(2)(理)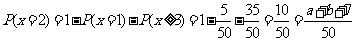
 ①;---------9分
又
①;---------9分
又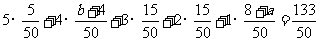
 ②; - --------11分
②; - --------11分
结合①②可得 ,
,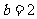 .
---------12分
.
---------12分
13、(重庆市大足中学2009年高考数学模拟试题)甲、乙两个箱子中装有大小相同的小球,甲箱中有2个红球和2个黑球,乙箱中装有2个黑球和3个红球,现从甲箱和乙箱中各取一个小球并且交换。
(1)求交换后甲箱中刚好有两个黑球的概率。(6分)
(2)设交换后甲箱中黑球的个数为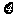 ,
,
求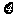 的分布列和数学期望。(6分)
的分布列和数学期望。(6分)

12、(天津市汉沽一中2008~2009学年度高三第四次月考试题)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入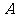 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
 (Ⅰ)求小球落入
(Ⅰ)求小球落入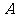 袋中的概率
袋中的概率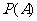 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记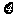 为落入
为落入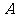
袋中小球的个数,试求 的概率和
的概率和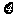 的数学期望
的数学期望 .
.
解: (Ⅰ)解法一:记小球落入 袋中的概率
袋中的概率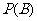 ,则
,则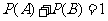 ,
,
由于小球每次遇到黑色障碍物时一直向左或者一直向右下落,小球将落入 袋,所以
袋,所以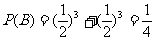 ‘………………………………………………………………… 2分
‘………………………………………………………………… 2分
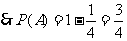 . ……………………………………………………………… 5分
. ……………………………………………………………… 5分
解法二:由于小球每次遇到黑色障碍物时,有一次向左和两次向右或两次向左和一次向右下落时小球将落入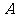 袋.
袋.
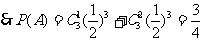 ,
……………………………… 5分
,
……………………………… 5分
(Ⅱ)由题意,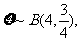 所以有 ……………………………………………… 7分
所以有 ……………………………………………… 7分
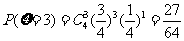 ,
……………………………………… 10分
,
……………………………………… 10分
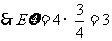 .
………………………………
12分
.
………………………………
12分
11、(辽宁省大连市第二十四中学2009届高三高考模拟)有一种舞台灯,外形是正六棱柱ABCDEF-A1B1C1D1E1F1,在其每一个侧面上(不在棱上)安装5只颜色各异的彩灯,假若每只灯正常发光的概率是0.5,若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面. 假定更换一个面需100元,用ξ表示维修一次的费用.
(1)求面ABB1A1需要维修的概率;
(2)写出ξ的分布列,并求ξ的数学期望.
解:(1)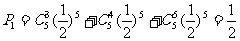 …………………………6分
…………………………6分
(2)因为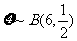
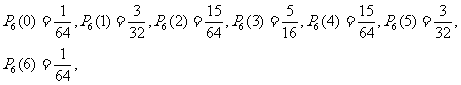
|
ξ |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
|
P |
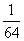 |
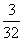 |
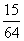 |
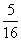 |
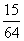 |
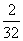 |
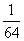 |
………………………………………………10分
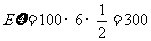 (元)………………………………………………12分
(元)………………………………………………12分
10、(湖南省衡阳市八中2009届高三第三次月考试题)2008年中国北京奥运会吉祥物由5个“中国福娃”组成,分别叫贝贝、晶晶、欢欢、迎迎、妮妮。现有8个相同的盒子,每个盒子中放一只福娃,每种福娃的数量如下表:
|
福娃名称 |
贝贝 |
晶晶 |
欢欢 |
迎迎 |
妮妮 |
|
数量 |
1 |
2 |
3 |
1 |
1 |
从中随机地选取5只。
(1)求选取的5只恰好组成完整“奥运吉祥物”的概率;
(2)若完整地选取奥运会吉祥物记100分;若选出的5只中仅差一种记80分;差两种记60分;以此类推。设ξ表示所得的分数,求ξ的分布列和期望值。
解:(1)选取的5只恰好组成完整“奥运吉祥物”的概率
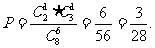
(2)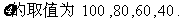
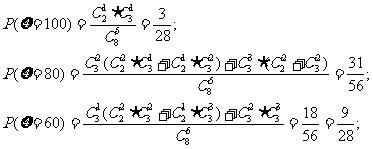
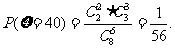 ξ的分布列为:
ξ的分布列为:
|
ξ |
100 |
80 |
60 |
40 |
|
P |
 |
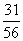 |
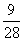 |
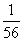 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com