
(1)整式不等式的解法(根轴法).
步骤:正化,求根,标轴,穿线(偶重根打结),定解.
特例① 一元一次不等式ax>b解的讨论:对ax>b形式的不等式,当a>0时解集为 当a<0时解集为
当a<0时解集为 。当a=0且b<0时解集为R当a=0且b≥0时,解集为
。当a=0且b<0时解集为R当a=0且b≥0时,解集为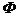 ;
;
因未限制a的符号,故ax<b可改为-ax>-b不必另行列出。
②一元二次不等式我们总可化为ax2+bx+c>0和ax2+bx+c+<0(a>0)两形式之一,记△=b2-4ac。
|
|
ax2+bx+c>0 |
ax2+bx+c+<0 |
|
△<0 |
R |
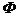 |
|
△=0 |
{x|x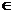 R且x R且x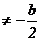 } } |
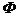 |
|
△>0 |
 |
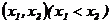 |
(2)分式不等式的解法:先移项通分标准化,则
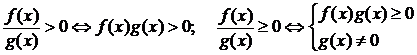
3.若集合M={y|y=2-x},P={y|y=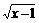 },那么集合M∩P=
},那么集合M∩P=
A.{y|y>1} B.{y|y≤1} C.{y|y>0} D.{y|y≥0}
2.已知集合M={x|-1<x<2},N={y|y=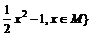 ,则M∩N=
,则M∩N=
A.{a|-1≤a<2 B.{a|-1<a<2} C.{a|-1<a<1} D.φ
1.含有三个实数的集合可表示为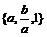 ,也可表示为{a2,a+b,0},则a2003+b2003的值为
,也可表示为{a2,a+b,0},则a2003+b2003的值为
A.0 B.1 C.-1 D.±1
例1.已知函数f(x)=x+1,g(x)=x2,D=[-1,a](a>-1),求使集合A= 与集合B=
与集合B=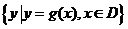 相等的实数a的值.
相等的实数a的值.
例2.已知集合A=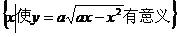 ,集合B=
,集合B=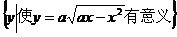 ,A=B是否可能成立?如可能成立,求出使A=B的a的取值范围,如不可能成立,说明理由.
,A=B是否可能成立?如可能成立,求出使A=B的a的取值范围,如不可能成立,说明理由.
例3.定义域为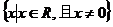 的奇函数f(x)在(0,+∞)上单调递增,而f(1)=0,设函数g(x)=sin2x+kcosx-2k(x∈[0,
的奇函数f(x)在(0,+∞)上单调递增,而f(1)=0,设函数g(x)=sin2x+kcosx-2k(x∈[0, ])集合M=
])集合M=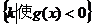 N=
N=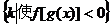 ,求M∩N.
,求M∩N.
例4.已知集合A=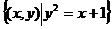 ,B=
,B=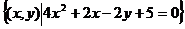 ,C=
,C=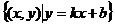 ,是否存在正整数k与b,使(A∪B)∩C=φ?
,是否存在正整数k与b,使(A∪B)∩C=φ?
3.(05浙江卷)设f(n)=2n+1(n∈N),P={1,2,3,4,5},Q={3,4,5,6,7},记 ={n∈N|f(n)∈P},
={n∈N|f(n)∈P},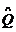 ={n∈N|f(n)∈Q},则(
={n∈N|f(n)∈Q},则( ∩
∩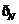
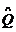 )∪(
)∪(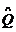 ∩
∩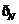
 )=( A
)
)=( A
)
(A) {0,3} (B){1,2} (C) (3,4,5) (D){1,2,6,7}
2.(05江西卷)设集合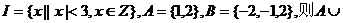 (
(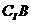 )=(D)
)=(D)
A.{1} B.{1,2} C.{2} D.{0,1,2}
1.(05上海卷)已知集合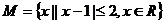 ,
,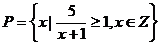 ,则
,则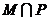 等于
(B)
等于
(B)
A.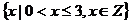 B.
B.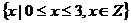
C.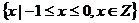 D.
D.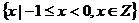
5.定义A-B={x|x∈A且x B},若M={1,2,3,4,5},N={2,3,6},则N-M等于 ( )
B},若M={1,2,3,4,5},N={2,3,6},则N-M等于 ( )
A.M B.N C.{1,4,5} D.{6}
4.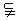 设集合P={a,b,c,d},Q={A|A P},则集合Q的元素个数__________________.
设集合P={a,b,c,d},Q={A|A P},则集合Q的元素个数__________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com