2009.3
命题:梅红卫(台州一中) 应福贵(仙居中学)
审题:王建华(黄岩中学)
注意事项:
1. 本卷共4页,三大题,22小题,满分150分,考试时间120分钟;
2. 用蓝、黑色水笔或圆珠笔书写答案,考试结束只需将答案纸交回.
参考公式:
球的表面积公式  棱柱的体积公式V=Sh
棱柱的体积公式V=Sh
球的体积公式  其中S表示棱柱的底面积,h表示棱柱的高
其中S表示棱柱的底面积,h表示棱柱的高
其中R表示球的半径
棱台的体积公式
棱锥的体积公式 V= Sh
其中S1,
S2分别表示棱台的上底、下底面积,
Sh
其中S1,
S2分别表示棱台的上底、下底面积,
h表示棱台的高
其中S表示棱锥的底面积,h表示棱锥的高 如果事件A,B互斥,那么
一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
5. 已知向量 的夹角为
的夹角为 ,
, 则
则
(A) 7 (B) 6 (C)5 (D)4
试题详情
 6. 一个空间几何体的三视图及部分数据如图所示,
6. 一个空间几何体的三视图及部分数据如图所示,
则这个几何体的体积是
试题详情
(A) (B)1
(B)1
试题详情
(C) (D)2
(D)2
试题详情
7. 现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.
③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是
(A)①简单随机抽样,②系统抽样,③分层抽样.
(B)①简单随机抽样,②分层抽样,③系统抽样.
(C)①系统抽样,②简单随机抽样,③分层抽样.
(D)①分层抽样,②系统抽样,③简单随机抽样.
试题详情
试题详情
(A)4
(B) 1或 (C)
(C) 或4 (D)1,
或4 (D)1,  或4
或4
试题详情
试题详情
(A)0 (B)1 (C)-1 (D)-1004.5
试题详情
试题详情
(A)2
(B)1 (C) (D)
(D)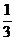
试题详情
二.填空题:本大题共7小题,每小题4分,共28分. 把答案填在答题卡的相应位置.
试题详情
12. 已知直线 和两个不同的平面
和两个不同的平面 ,则下列命题中错误的是 ▲
(请写出错误命题的序号).
,则下列命题中错误的是 ▲
(请写出错误命题的序号).
试题详情
试题详情
试题详情
试题详情
若输出 的值是4,
的值是4,
试题详情
则输入的实数 = ▲
.
= ▲
.
试题详情
试题详情
命题 是命题
是命题 的否定,则命题
的否定,则命题
试题详情
试题详情
15.已知双曲线 的右焦点是椭圆
的右焦点是椭圆 的一个顶点,则
的一个顶点,则
试题详情
 = ▲ .
= ▲ .
试题详情
试题详情
17.有一堆除颜色外其它特征都相同的红白两种颜色的球若干个,已知红球的个数比白球多,
试题详情
但比白球的2倍少,若把每一个白球都记作数值2,每一个红球都记作数值3,则所有球的数值的总和等于60.现从中任取一个球,则取到红球的概率等于 ▲
.
试题详情
三.解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
试题详情
 .
.
试题详情
(Ⅰ)求角 的大小;
的大小;
试题详情
试题详情
试题详情
19.(本题满分14分)已知四棱锥 中,
中, ⊥底
⊥底
试题详情
试题详情
 ,
, .
.
试题详情
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
试题详情
(Ⅱ)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
试题详情
试题详情
(Ⅰ)求证: ;
;
试题详情
试题详情
试题详情
(Ⅰ)求 的解析式;
的解析式;
试题详情
(Ⅱ)已知实数 能使函数
能使函数 上既能取到极大值,又能取到极小值,记所有的实数
上既能取到极大值,又能取到极小值,记所有的实数 组成的集合为M.请判断函数
组成的集合为M.请判断函数 的零点个数.
的零点个数.
试题详情
试题详情
都是圆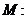
 的切线.
的切线.
试题详情
试题详情
试题详情
1-10.CDBBA CACBD
11. 12. ①③④ 13.-2或1 14.
12. ①③④ 13.-2或1 14.  、
、 15.2 16.
15.2 16.  17.
17. .
.
18.
解:(1)由已知
 7分
7分
(2)由 10分
10分
由余弦定理得 14分
14分
19.(1)证明:∵PA⊥底面ABCD,BC 平面AC,∴PA⊥BC, 3分
平面AC,∴PA⊥BC, 3分
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC. 5分
(2)解:过C作CE⊥AB于E,连接PE,
∵PA⊥底面ABCD,∴CE⊥面PAB,
∴直线PC与平面PAB所成的角为 , 10分
, 10分
∵AD=CD=1,∠ADC=60°,∴AC=1,PC=2,
 中求得CE=
中求得CE= ,∴
,∴ . 14分
. 14分
 20.解:(1)由
20.解:(1)由 ①,得
①,得 ②,
②,
②-①得: . 4分
. 4分
(2)由 求得
求得 . 7分
. 7分
∴ ,
, 11分
11分

∴ .
14分
.
14分
21.解:
(1)由 得c=1 1分
得c=1 1分
 , 4分
, 4分
