S← 1 For I from 1 to 9
step 2 S←S + I End for Print S
试题详情
试题详情
试题详情
试题详情
试题详情
9.将一枚骰子抛掷两次,若先后出现的点数分别为 ,则方程 ,则方程 有实根的概率 有实根的概率 为 ▲ . 高三数学试卷?第1页(共4页) 试题详情
试题详情
则 ▲ . ▲ . 试题详情
试题详情
12.在一个密封的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围是
▲ . 试题详情
试题详情
试题详情
甲说:“可视 为变量, 为变量, 为常量来分析”. 为常量来分析”. 试题详情
乙说:“不等式两边同除以 2,再作分析”. 2,再作分析”. 试题详情
丙说:“把字母 单独放在一边,再作分析”. 单独放在一边,再作分析”. 试题详情
参考上述思路,或自已的其它解法,可求出实数 的取值范围是 ▲ . 的取值范围是 ▲ . 试题详情
二、解答题:(本大题共6小题,共90分)
试题详情
已知向量a=(sin( +x), +x), cosx),b =(sinx,cosx), f(x)=a?b. cosx),b =(sinx,cosx), f(x)=a?b. ⑴求f(x)的最小正周期和单调增区间; 试题详情
⑵如果三角形ABC中,满足f(A)= ,求角A的值. ,求角A的值. 高三数学试卷?第2页(共4页) 试题详情
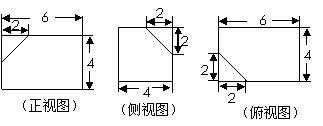
16.(本题满分14分,第1问4分,第2问5分,第3问5分) 如下的三个图中,分别是一个长方体截去一个角所得多面体的直观图以及它的主视图和左视图(单位:cm) (1)按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积; 试题详情
试题详情
试题详情
试题详情
已知函数 ,常数 ,常数 . . 试题详情
试题详情
试题详情
18.(本题满分15分,第1问5分,第2问5分,第3问5分) 试题详情
试题详情
试题详情
 (3)过M点作直线 (3)过M点作直线 与圆相切于点N,设(2)中椭圆的两个焦点分别为F1,F2,求三角形 与圆相切于点N,设(2)中椭圆的两个焦点分别为F1,F2,求三角形 面积. 面积.
高三数学试卷?第3页(共4页) 试题详情
19.(本题满分16分,第1问4分,第2问6分,第3问6分) 试题详情
试题详情
(1)求数列 的通项公式; 的通项公式; 试题详情
(2)若函数 求函数 求函数 的最小值; 的最小值; 试题详情
试题详情
 对于一切不小于2的自然数 对于一切不小于2的自然数 恒成立? 恒成立?
试题详情
若存在,写出 的解析式,并加以证明;若不存在,试说明理由. 的解析式,并加以证明;若不存在,试说明理由. 试题详情
20.(本题满分16分,第1问4分,第2问6分,第3问6分) 试题详情
已知函数 ,过点P(1,0)作曲线 ,过点P(1,0)作曲线 的两条切线PM,PN,切点分别为M,N. 的两条切线PM,PN,切点分别为M,N. 试题详情
(1)当 时,求函数 时,求函数 的单调递增区间; 的单调递增区间; 试题详情
(2)设|MN|= ,试求函数 ,试求函数 的表达式; 的表达式; 试题详情
(3)在(2)的条件下,若对任意的正整数 ,在区间 ,在区间 内,总存在m+1个数 内,总存在m+1个数 使得不等式 使得不等式 成立,求m的最大值. 成立,求m的最大值. 高三数学试卷?第4页(共4页) 2009届启东市高三第一学期第二次质量检测 数 学 (理科加试题) (加试题每小题10分,共40分,考试时间30分钟) 试题详情
试题详情
已知二阶矩阵A的属于特征值-1的一个特征向量为 ,属于特征值3的一个特征向量为 ,属于特征值3的一个特征向量为 ,求矩阵A. ,求矩阵A. 试题详情
试题详情
在极坐标系中,从极点O作直线与另一直线 相交于点M,在OM上取一点P,使 相交于点M,在OM上取一点P,使 . . (1)求点P的轨迹方程; 试题详情
(2)设R为 上任意一点,试求RP的最小值. 上任意一点,试求RP的最小值. 试题详情
试题详情
(1)求n,p的值并写出 的分布列; 的分布列; (2)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率. 试题详情
4.设 , , , , 试题详情
试题详情
试题详情
(3) 展开式中 展开式中 的系数是19,当 的系数是19,当 , , 变化时,求 变化时,求 系数的最小值. 系数的最小值. 高三数学试卷(理科加试题)?第1页(共1页) 数 学 答 案 试题详情
一、填空题:
试题详情
试题详情
13.0.5 14. 试题详情
二、解答题:
试题详情
T=π,2 kπ- ≤2x+ ≤2x+ ≤2 kπ+ ≤2 kπ+ ,k∈Z, ,k∈Z, 最小正周期为π,----------------------------------------------------5分 试题详情
单调增区间[kπ- ,kπ+ ,kπ+ ],k∈Z.-----------------------------------------------------7分 ],k∈Z.-----------------------------------------------------7分 试题详情
试题详情
试题详情
试题详情
  ------------4分 ------------4分
试题详情
试题详情
(3)证明:在长方体 中, 中, 试题详情
连结 ,则 ,则 . . 试题详情
试题详情
试题详情
试题详情
 , ,
试题详情
试题详情
故 在 在 上单调递增.或求导方法.--------------------------7分 上单调递增.或求导方法.--------------------------7分 试题详情
(2)因为 在 在 上单调递增, 上单调递增, 试题详情
试题详情
即 是方程 是方程 的两个不等的正根 的两个不等的正根 试题详情
 有两个不等的正根.-------------------------13分 有两个不等的正根.-------------------------13分
试题详情
试题详情
试题详情
设 的方程为 的方程为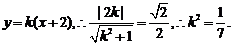 试题详情
 的方程为 的方程为 ----------------------------------------------------------------5分 ----------------------------------------------------------------5分
试题详情
(2)设椭圆方程为 ,半焦距为c,则 ,半焦距为c,则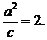 试题详情
试题详情
试题详情
当 时, 时, 试题详情
所求椭圆方程为 -------------------------------------------------------------10分 -------------------------------------------------------------10分 试题详情
试题详情
N点的坐标为 ,------------------- 11分 ,------------------- 11分 试题详情
若椭圆为 其焦点F1,F2 其焦点F1,F2 试题详情
分别为点A,B故 ,-----------------------------------13分 ,-----------------------------------13分 试题详情
若椭圆为 ,其焦点为 ,其焦点为 , , 试题详情
此时 -------------------------------------------15分 -------------------------------------------15分 试题详情
19.解:(1)由点P 在直线 在直线 上, 上, 试题详情
即 ,------------------------------------------------------------------------2分 ,------------------------------------------------------------------------2分 试题详情
且 ,数列{ ,数列{ }是以1为首项,1为公差的等差数列 }是以1为首项,1为公差的等差数列 试题详情
试题详情
(2) 试题详情
 ---------------------6分 ---------------------6分 试题详情
试题详情
试题详情
试题详情
 , , 试题详情
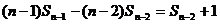
…… 试题详情
试题详情
试题详情
 ,n≥2------------------14分 ,n≥2------------------14分
试题详情
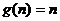
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----16分 试题详情
20. 解:(1)当  --------2分 --------2分 试题详情
试题详情
(2)设M、N两点的横坐标分别为 、 、 , ,
|
试题详情
同理,由切线PN也过点(1,0),得 (2)---------------6分 (2)---------------6分 试题详情
由(1)、(2),可得 的两根, 的两根, 试题详情
 ------------------------------------------------------8分 ------------------------------------------------------8分 试题详情
试题详情
试题详情
把(*)式代入,得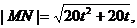 试题详情
因此,函数 ----------------10分 ----------------10分 试题详情
(3)易知 上为增函数, 上为增函数, 试题详情
试题详情
 ------------12分 ------------12分 试题详情
试题详情
试题详情
由于m为正整数, . --------------------------------------------------14 分 . --------------------------------------------------14 分 试题详情
又当 因此,m的最大值为6. ----------------------------------------------16分 2009届启东市高三第一学期第二次质量检测 数 学 加 试
题 答 案 试题详情
试题详情
即 ,
---------------------------------------------------------------------6分 ,
---------------------------------------------------------------------6分 试题详情
解之得: -----------------------------------------------------------------8分
-----------------------------------------------------------------8分 试题详情
∴A= --------------------------------------------------------------------------10分 --------------------------------------------------------------------------10分 试题详情
试题详情
(2) ------------------------------------------------------------------------10分
------------------------------------------------------------------------10分 试题详情
3.解:(1)由 得 得 ,------------3分 ,------------3分 试题详情
从而 , ,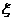 的分布列为 的分布列为 试题详情
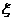
0 1 2 3 4 5 6 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情

-------5分 试题详情
(2)记”需要补种沙柳”为事件A,则 得 得 --10分 --10分 试题详情
试题详情
(2) , , -------------------------------------------------6分 -------------------------------------------------6分 试题详情
试题详情
试题详情
所以,当 或 或 时, 时, 展开式中 展开式中 的系数最小,为81.----10分 的系数最小,为81.----10分 试题详情
| | | 
 ,则
,则 =_____▲_____.
=_____▲_____. 在点P处的切线平行于直线3x-y=0,则点P的坐标为
▲ .
在点P处的切线平行于直线3x-y=0,则点P的坐标为
▲ . 4.如图所示,墙上挂有一边长为
4.如图所示,墙上挂有一边长为 的正方形木板,它的四个角的空白部分
的正方形木板,它的四个角的空白部分 的圆弧,某人向此板投镖,假设
的圆弧,某人向此板投镖,假设 ,若
,若 ,则实数
,则实数 的取值范围是 ▲ .
的取值范围是 ▲ .