
1 如果y=cosx是增函数,且y=sinx是减函数,那么x的终边在( )
如果y=cosx是增函数,且y=sinx是减函数,那么x的终边在( )
A 第一象限 B
第一象限 B 第二象限 C
第二象限 C 第三象限 D
第三象限 D 第四象限
第四象限
2 在[-π,π]上既是增函数,又是奇函数的是( )
在[-π,π]上既是增函数,又是奇函数的是( )
A y=sin
y=sin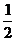 x B
x B y=cos
y=cos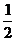 x C
x C y=-sin
y=-sin x D
x D y=sin2x
y=sin2x
3 函数y=sin(-2x)的单调减区间是( )
函数y=sin(-2x)的单调减区间是( )
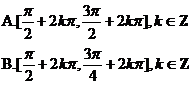
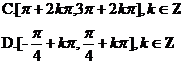
4 函数y=log2sinx的单调减区间是
函数y=log2sinx的单调减区间是

5 函数f(x)=cos2x+2的递增区间是
函数f(x)=cos2x+2的递增区间是

6 若f(x)=x2+bx+c对任意实数x都有f(1+x)=f(1-x),则f(cos1)与f(cos
若f(x)=x2+bx+c对任意实数x都有f(1+x)=f(1-x),则f(cos1)与f(cos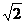 )的大小关系是
)的大小关系是

1 判断正误
判断正误
①y=Asinωx的最大值是A,最小值是-A.(×)
②y=Asinωx的周期是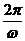
 (×)
(×)
③y=-3sin4x的振幅是3,最大值为3,最小值是-3 (√)
(√)
2 用图象变换的方法在同一坐标系内由y=sinx的图象画出函数y=-
用图象变换的方法在同一坐标系内由y=sinx的图象画出函数y=-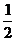 sin(-2x)的图象
sin(-2x)的图象
|
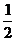 sin(-2x)=
sin(-2x)=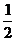 sin2x作图过程,
sin2x作图过程,
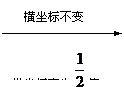
 y=sinx
y=sin2x
y=
y=sinx
y=sin2x
y=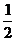 sin2x
sin2x
评述:先化简后画图
3 下列变换中,正确的是
下列变换中,正确的是
A 将y=sin2x图象上的横坐标变为原来的2倍(纵坐标不变)即可得到
将y=sin2x图象上的横坐标变为原来的2倍(纵坐标不变)即可得到
y=sinx的图象
B 将y=sin2x图象上的横坐标变为原来的
将y=sin2x图象上的横坐标变为原来的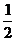 倍(纵坐标不变)即可得到
倍(纵坐标不变)即可得到
y=sinx的图象
C 将y=-sin2x图象上的横坐标变为原来的
将y=-sin2x图象上的横坐标变为原来的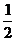 倍,纵坐标变为原来的相反数,即得到y=sinx的图象
倍,纵坐标变为原来的相反数,即得到y=sinx的图象
D 将y=-3sin2x图象上的横坐标缩小一倍,纵坐标扩大到原来的
将y=-3sin2x图象上的横坐标缩小一倍,纵坐标扩大到原来的 倍,且变为相反数,即得到y=sinx的图象
倍,且变为相反数,即得到y=sinx的图象
答案:A
2.若ω<0则可用诱导公式将符号“提出”再作图
ω决定了函数的周期,这一变换称为周期变换
1.函数y=sinωx, xÎR (ω>0且ω¹1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的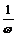 倍(纵坐标不变)
倍(纵坐标不变)
3.若A<0
可先作y=-Asinx的图象 ,再以x轴为对称轴翻折
A称为振幅,这一变换称为振幅变换
例2 画出函数y=sin2x
xÎR;y=sin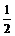 x xÎR的图象(简图)
x xÎR的图象(简图)
解:函数y=sin2x,x∈R的周期T=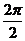 =π
=π
我们先画在[0,π]上的简图,在[0, p]上作图,列表:
|
2x |
0 |
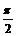 |
p |
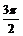 |
2p |
|
x |
0 |
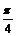 |
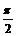 |
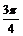 |
p |
|
y=sin2x |
0 |
1 |
0 |
-1 |
0 |
作图:
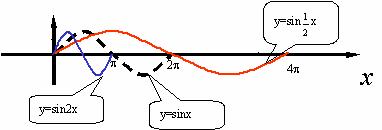
函数y=sin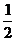 x,x∈R的周期T=
x,x∈R的周期T=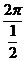 =4π
=4π
我们画[0,4π]上的简图,列表:
 |
0 |
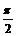 |
p |
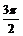 |
2p |
|
x |
0 |
p |
2p |
3p |
4p |
sin |
0 |
1 |
0 |
-1 |
0 |
(1)函数y=sin2x,x∈R的图象,可看作把y=sinx,x∈R上所有点的横坐标缩短到原来的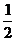 倍(纵坐标不变)而得到的
倍(纵坐标不变)而得到的
(2)函数y=sin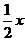 ,x∈R的图象,可看作把y=sinx,x∈R上所有点的横坐标伸长到原来的2倍(纵坐标不变)而得到
,x∈R的图象,可看作把y=sinx,x∈R上所有点的横坐标伸长到原来的2倍(纵坐标不变)而得到
引导, 观察启发: 与y=sinx的图象作比较
2.它的值域[-A, A] 最大值是A, 最小值是-A
例1画出函数y=2sinx xÎR;y=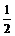 sinx xÎR的图象(简图)
sinx xÎR的图象(简图)
解:画简图,我们用“五点法”
∵这两个函数都是周期函数,且周期为2π
∴我们先画它们在[0,2π]上的简图 列表:
列表:
|
x |
0 |
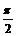 |
p |
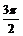 |
2p |
|
sinx |
0 |
1 |
0 |
-1 |
0 |
|
2sinx |
0 |
2 |
0 |
-2 |
0 |
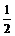 sinx sinx |
0 |
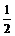 |
0 |
-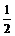 |
0 |
作图:
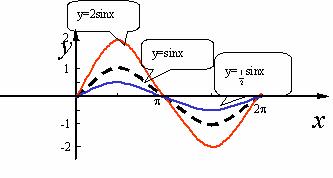
(1)y=2sinx,x∈R的值域是[-2,2]
图象可看作把y=sinx,x∈R上所有点的纵坐标伸长到原来的2倍而得(横坐标不变)
(2)y=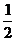 sinx,x∈R的值域是[-
sinx,x∈R的值域是[-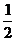 ,
,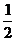 ]
]
图象可看作把y=sinx,x∈R上所有点的纵坐标缩短到原来的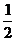 倍而得(横坐标不变)
倍而得(横坐标不变)
引导,观察,启发:与y=sinx的图象作比较,结论:
1.y=Asinx,xÎR(A>0且A¹1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的
21. (13分) 已知函数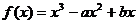 .
.
(1)若函数 在点(2,
在点(2,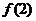 )的切线方程为
)的切线方程为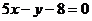 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(2)若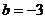 ,
,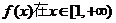 上是增函数,求实数
上是增函数,求实数 的取值范围。
的取值范围。
20. (13分)已知奇函数 的定义域是
的定义域是 ,且
,且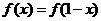 ,当0≤x≤
,当0≤x≤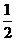 时,
时,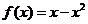 .
.
(1)求证: 是周期函数;
是周期函数;
(2)求 在区间
在区间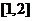 上的解析式;
上的解析式;
(3)求方程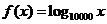 的根的个数.
的根的个数.
19. (13分)在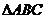 中,
中,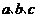 分别为角
分别为角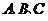 的对边,且满足
的对边,且满足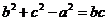 .
.
(1)求角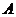 的值;
的值;
(2)若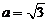 ,设角
,设角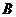 的大小为
的大小为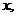
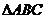 的周长为
的周长为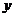 ,求
,求 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com