
2、影响水的电离平衡的因素
⑴温度 ⑵酸、碱
⑶易水解的盐
[思考]分析下列条件的改变对水的电离平衡的影响:
|
项目 条件 |
平衡移 动方向 |
C(H+) 变化 |
C(OH-) 变化 |
C(H+)与C(OH-) 大小比较 |
Kw |
溶液 酸碱性 |
|
升温 |
|
|
|
|
|
|
|
加入少量H2SO4 |
|
|
|
|
|
|
|
加入少量NaOH |
|
|
|
|
|
|
|
加入少量Na2CO3 |
|
|
|
|
|
|
|
加入少量FeCl3 |
|
|
|
|
|
|
[例1]纯水在25℃和80℃时的H+浓度,前后两个量的大小关系为( )
A. 大于 B. 等于 C. 小于 D. 不能确定
1、水是一种 电解质,其电离方程式为 ,
水的离子积Kw=
Kw只随温度变化而不随浓度变化,水的电离是 热过程,25℃时,Kw=
15.(2008·宁夏、海南)设函数f(x)=ax+(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3.
(1)求f(x)的解析式;
(2)证明:函数y=f(x)的图象是一个中心对称图形,并求其对称中心;
(3)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,并求出此定值.
(1)解:f′(x)=a-,
于是
解得或
因a,b∈Z,故f(x)=x+.
(2)证明:已知函数y1=x,y2=都是奇函数.
所以函数g(x)=x+也是奇函数,其图象是以原点为中心的中心对称图形.
而f(x)=x-1++1.
可知,函数g(x)的图象按向量a=(1,1)平移,即得到函数f(x)的图象,故函数f(x)的图象是以点(1,1)为中心的中心对称图形.
(3)证明:在曲线上任取一点
.
由f′(x0)=1-知,过此点的切线方程为
y-=(x-x0).
令x=1得y=,切线与直线x=1交点为.
令y=x得y=2x0-1,
切线与直线y=x交点为(2x0-1,2x0-1).
直线x=1与直线y=x的交点为(1,1).
从而所围三角形的面积为
|2x0-1-1|
=·=2
所以所围成三角形的面积为定值2.
14.(2008·山东师大附中)已知f(x)是定义在(0,+∞)上的单调递增函数,对于任意的m、n[m、n∈(0,+∞)]满足f(m)+f(n)=f(mn),且a、b(0<a<b)满足|f(a)|=|f(b)|=2.
(1)求f(1);
(2)若f(2)=1,解不等式f(x)<2;
(3)求证:3<b<2+.
解:(1)令m=n=1,由f(m)+f(n)=f(mn),得f(1)+f(1)=f(1).
∴f(1)=0.
(2)∵f(2)=1,
∴f(x)<2=1+1=f(2)+f(2)=f(4).
又f(x)在(0,+∞)上单调递增,
∴0<x<4,∴f(x)<2的解集为(0,4) .
(3)∵f(1)=0,f(x)在(0,+∞)上单调递增,
∴x∈(0,1)时,f(x)<0;
x∈(1,+∞)时,f(x)>0.
又|f(a)|=|f(b)|,
∴f(a)=f(b)或f(a)=-f(b).
∵0<a<b,∴f(a)=-f(b),
∴f(a)+f(b)=f(ab)=0,
∴ab=1,∴0<a<1<b.
又∵|f(b)|=2,
且b>1,>=1,
∴f(b)=2f,
∴4b=a2+2ab+b2,
∴4b-b2-2=a2,考虑到0<a<1,
∴0<4b-b2-2<1,又b>1,
∴3<b<2+.
13.(2008·北京海淀)
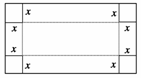
今有一长2米,宽1米的矩形铁皮,如右图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起,做成一个无盖的长方体水箱(接口连接问题不考虑).
(1)求水箱容积的表达式f(x),并指出函数f(x)的定义域;
(2)若要使水箱容积不大于4x3立方米的同时,又使得底面积最大,求x的值.
解:(1)由已知该长方体水箱高为x米,底面矩形长为(2-2x)米,宽(1-2x)米.
∴该水箱容积为f(x)=(2-2x)(1-2x)·x
f(x)=4x3-6x2+2x,
其中正数x满足
∴0<x<.
∴所求函数f(x)的定义域为
.
(2)由f(x)≤4x3,得x≤0或x≥.
∵函数f(x)的定义域为.
∴≤x<.
此时底面积为S(x)=(2-2x)(1-2x)
=4x2-6x+2,x∈.
由S(x)=42-,
可知S(x)在上是减函数,
∴x=.
答:满足条件的x为米.
12.(2009·重庆市一测)某厂家拟在2009年举行促销活动.经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用t(t≥0)万元满足x=4-(k为常数).如果不搞促销活动,则该产品的年销售量只能是1万件.已知2009年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分).
(1)将该厂家2009年该产品的利润y万元表示为年促销费用t万元的函数;
(2)该厂家2009年的促销费用投入多少万元时,厂家利润最大?
解:(1)由题意可知1=4-得k=3,故x=4-.
y=1.5··x-(6+12x)-t=3+6x-t=3+6(4-)-t=27--t(t≥0).
(2)y=27--t=27.5-(+t+)≤27.5-2=21.5.
当且仅当=t+,即t=2.5时,y取得最大值.
故2009年的促销费用投入2.5万元时,厂家利润最大.
11.(2008·石家庄二测)已知函数y=f(x)是R上的偶函数,对于x∈R都有f(x+6)=f(x)+f(3)成立,且f(-4)=-2,当x1,x2∈[0,3],且x1≠x2时,都有>0.则给出下列命题:
①f(2008)=-2;
②函数y=f(x)图象的一条对称轴为x=-6;
③函数y=f(x)在[-9,-6]上为减函数;
④方程f(x)=0在[-9,9]上有4个根;
其中所有正确命题的序号为________.
答案:①②③④
解析:f(x+6)=f(x)+f(3),f(3)=0,
则f(x+6)=f(x),6为函数的一个周期,又函数y=f(x)是R上的偶函数,且f(-4)=-2,则f(4)=-2,当x1,x2∈[0,3],且x1≠x2时,都有>0,函数在区间[0,3]上为增函数.对于①,f(2008)=f(4+6×334)=f(4)=-2,①正确;对于②,由奇偶性和周期性得函数y=f(x)图象的一条对称轴为x=-6,则②正确;对于③,由周期性知函数y=f(x)在[-6,-3]上为增函数,又函数y=f(x)图象的一条对称轴为x=-6,则函数y=f(x)在[-9,-6]上为减函数,③正确;对于④,由于f(3)=0,根据奇偶性和周期性得f(-3)=0,f(9)=0,f(-9)=0,则方程f(x)=0在[-9,9]上有4个根,④正确;综上所述,①②③④正确,故填①②③④.
10.(2008·重庆一模)将函数f(x)=的图象向左平移一个单位,再向下平移一个单位后,得到函数g(x)的图象,则g(1)+2g(2)+3g(3)=________.
答案:9
解析:函数f(x)=的图象向左平移一个单位,再向下平移一个单位后,得到函数g(x)=f(x+1)-1=-1=,则g(1)+2g(2)+3g(3)=9,故填9.
9.(2009·江西九校联考)给出下列四个命题:①函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0;②函数y=2-x的反函数是y=-log2x;③若函数f(x)=lg(x2+ax-a)的值域是R,则a≤-4或a≥0;④若函数y=f(x-1)是偶函数,则函数y=f(x)的图象关于直线x=1对称.其中所有正确命题的序号是________.
答案:①②③
解析:依题意,因为f(x)=x|x|+bx+c为奇函数,所以f(-x)=-x|x|-bx+c=-f(x)=-x|x|-bx-c,所以c=0,①正确;由y=2-x解得x=-log2y,即函数y=2-x的反函数为y=-log2x,②正确;函数f(x)=lg(x2+ax-a)的值域为R,则Δ=a2+4a≥0,解得a≤-4或a≥0,所以③正确;因为函数y=f(x-1)是偶函数,则图象关于y轴对称,y=f(x)的图象由函数y=f(x-1)的图象向左平移一个单位得到,则y=f(x)的图象关于直线x=-1对称,所以④错.
8.(2009·东北三校联考)设函数f(x)=,则(a≠b)的值为( )
A.a B.b
C.a、b中较小的数 D.a、b中较大的数
答案:C
解析:对a-b进行讨论,当a-b>0时,f(a-b)=-1,==b;当a-b<0时,f(a-b)=1,==a,所以上式的值为a、b中较小的数.选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com