
题目列表(包括答案和解析)
2.斜三角形中各元素间的关系:
如图6-29,在△ABC中,A、B、C为其内角,a、b、c分别表示A、B、C的对边。
(1)三角形内角和:A+B+C=π。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等
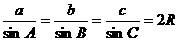 。
。
(R为外接圆半径)
(3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍
a2=b2+c2-2bccosA;b2=c2+a2-2cacosB;c2=a2+b2-2abcosC。
1.直角三角形中各元素间的关系:
如图,在△ABC中,C=90°,AB=c,AC=b,BC=a。
(1)三边之间的关系:a2+b2=c2。(勾股定理)
(2)锐角之间的关系:A+B=90°;
(3)边角之间的关系:(锐角三角函数定义)
sinA=cosB=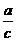 ,cosA=sinB=
,cosA=sinB=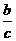 ,tanA=
,tanA=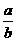 。
。
对本讲内容的考察主要涉及三角形的边角转化、三角形形状的判断、三角形内三角函数的求值以及三角恒等式的证明问题,立体几何体的空间角以及解析几何中的有关角等问题。今后高考的命题会以正弦定理、余弦定理为知识框架,以三角形为主要依托,结合实际应用问题考察正弦定理、余弦定理及应用。题型一般为选择题、填空题,也可能是中、难度的解答题
(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;
(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
19. 直线
直线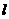 经过抛物线
经过抛物线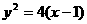 的焦点,且与准线成30
的焦点,且与准线成30 角,则直线
角,则直线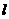 的斜截式方程是
的斜截式方程是
18.已知双曲线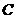 :
: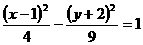 ,给出以下四个命题:
,给出以下四个命题:
① 双曲线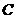 的渐近线方程是
的渐近线方程是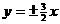 ;
;
② 直线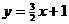 与双曲线
与双曲线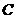 只有一个交点;
只有一个交点;
③ 将双曲线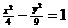 向左平移一个单位,并向上平移两个单位,可以得到双曲线
向左平移一个单位,并向上平移两个单位,可以得到双曲线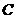 ;
;
④ 双曲线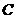 的一个焦点到一条渐近线的距离为3。
的一个焦点到一条渐近线的距离为3。
 其中所有正确命题的序号是
其中所有正确命题的序号是
17.椭圆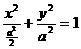 与连结
与连结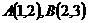 的线段没有公共点,则正数
的线段没有公共点,则正数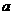 的取值范围是
的取值范围是

16.已知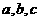 为某一直角三角形的三边,
为某一直角三角形的三边,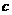 为斜边,若点
为斜边,若点 在直线
在直线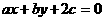 上,则
上,则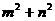 的最小值为
的最小值为

15.直线x-2y-3=0与圆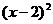 +
+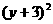 =9交于P、Q两点,则△POQ (O是原点)的面积等于(
)
=9交于P、Q两点,则△POQ (O是原点)的面积等于(
)
(A) 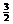 (B)
(B)
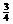
(C) 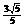 (D)
(D)
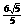
14.已知两点M(0,1).N(10,1)给出下列直线方程:
① 5x-3y-22=0 ② 5x-3y-52=0
③ x-y-4=0 ④ 4x-y-14=0
在直线上存在点P满足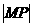 =
=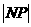 +6的所有直线方程是( )
+6的所有直线方程是( )
(A) ①②③ (B) ②④
(C) ①③ (D) ②③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com