
题目列表(包括答案和解析)
22、(本小题满分12分)
 如图:在四棱锥P-ABCD中,PA⊥平面ABCD,BA⊥AD,CD⊥AD,CD=2AB,E为PC的中点.
如图:在四棱锥P-ABCD中,PA⊥平面ABCD,BA⊥AD,CD⊥AD,CD=2AB,E为PC的中点.
(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)求证:EB∥平面PAD;
21、(本小题满分12分)
甲、乙、丙3人各进行1次射击,若3人击中目标的概率分别是 ,
, ,
, .求3人中至少有1人击中目标的概率.
.求3人中至少有1人击中目标的概率.
20、(本小题满分13分)
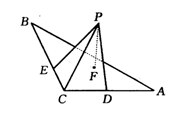 如图,在△ABC中,∠C是直角,平面ABC外一点P,PC=24cm点P到直线AC、BC的距离PD和PE都等于6
如图,在△ABC中,∠C是直角,平面ABC外一点P,PC=24cm点P到直线AC、BC的距离PD和PE都等于6 cm.
cm.
(Ⅰ)求点P到平面ABC的距离PF;
(Ⅱ)求PC与平面ABC所成的角.
19、(本小题满分13分)
已知:甲袋中有3个黑球,2个白球;乙袋中有4个黑球,5个白球.
(Ⅰ)从甲袋中任意取出两个球,求取得一黑一白的概率;
(Ⅱ)从甲、乙两袋中分别取出一个球,求取得一黑一白的概率.
18、(本小题满分13分)已知(x )n的展开式的前三项系数和为129,求展开式中含x的项.
)n的展开式的前三项系数和为129,求展开式中含x的项.
17、(13分)求证:如果一个平面与另一个平面的垂线平行,那么这两个平面互相垂直.
 已知:
已知:
求证:
证明:
16、已知:m,l是直线,α、β是平面,给出下列5个命题:
①若l垂直于α内两条相交直线,则l⊥α. ②若l∥α,则l平行于α内的所有直线.
③若m α,l
α,l β,且l⊥m,则α⊥β. ④若l
β,且l⊥m,则α⊥β. ④若l β,且l⊥α,则α⊥β. ⑤若m
β,且l⊥α,则α⊥β. ⑤若m α,l
α,l β,且α∥β,则m∥l.
β,且α∥β,则m∥l.
其中正确的命题序号是 .(写出所有真命题的序号)
15、233除以9的余数是 .
14、5名同学安排在周一至周五值日,每人一天,若甲同学不能排在星期一,乙同学不能排在星期五,则所有不同的排法种数为 .(用数字作答)
13、设地球半径为R,在南纬30°圈上有A、B两点,这两点的经度差为π,则A、B两点的球面距离为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com