3.(2007年1月海淀13)动点P在平面区域C₁: x² + y²≤2(| x | + | y |)内，动点Q在曲线C₂ :

(x – 4)² + (y – 4)² = 1上，则平面区域C₁的面积为__________，| PQ |的最小值为_________．

2．(2007年1月海淀8)动点P为椭圆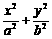= 1(a > b > 0)上异于椭圆顶点(±a，0)的一点，F₁、F₂为椭圆的两个焦点，动圆C与线段F₁P、F₁F₂的延长线及线段PF₂相切，则圆心C的轨迹为除去坐标轴上的点的

　　　　 A．一条直线　　　　　 B．双曲线的右支　 　　 C．抛物线　　　　　　　　 D．椭圆

1．(2007年1月海淀7)已知向量a = (2cos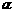，2sin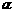)，b = (3cos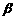，3sin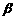)，若向量a与b的夹角为60°，则直线xcos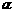– ysin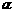+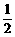= 0与圆(x – cos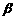)² + (y + sin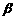)² =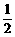的位置关系是

　　　　 A．相交　　　　　　　　　　 B．相切　　　　　　　　　　 　 C．相离　　　　　　　　　　　 D．相交且过圆心

7.现有一游戏：图上有若干个点和若干条线，甲提供若干个硬币，乙可以任意将这些硬币全部摆放在点上，并且指定一个目标定点u。现定义操作：从一个至少有两个硬币的点取走2个硬币，在它一个相邻的点上放回一个硬币。在指定的图下，甲最少提供多少个硬币，可以保证经过若干次操作，一定能使目标顶点u至少有一枚硬币？(1)图是一个包含5个点的线段；(2)图是一个包含7个点的圈。

6.现有100个集装箱，每个集装箱装2个物品。现在将集装箱的物品全部拆卸，并且所有物品被打乱顺序。问：最坏情况下，需要多少个集装箱再次把所有物品装好？

5.一条跑马比赛最多只能有8匹马参加，假设同一匹马参加每一场比赛的表现都是一样的。问：可以有不多于50场比赛，完全将64匹马的实力顺序排序吗？

4.现有一数字游戏：有1到100的数，2个人轮流写。设已经写下的数为a1,a2,a3,...,an。若一个数x能表示成x=x1a1+x2a2+...+xnan(x1,x2,...,xn为非负整数)，则这个数不能够被写。(如若3，5已被写，则8=3+5不能再写，13=3+5*2，9=3*3+5*0也不能再被写)现在甲和乙玩这个游戏，已知5，6已经被写，现在轮到甲写。问：谁有必胜策略？

3.求2+2e^(0.4i)+e^(1.2i)的模。

2.请找出一个含有根(2的开方+3的开立方)的整系数多项式。

1.有数条抛物线(线和线的内部)能够覆盖整个平面吗？证明你的结论。