13.　　 (96上海)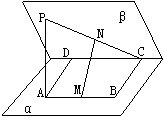如图，在二面角α－l－β中，A、B∈α，C、D∈l，ABCD为矩形，P∈β，PA⊥α，且PA＝AD，M、N依次是AB、PC的中点 ⑴求二面角α－l－β的大小； ⑵求证：MN⊥AB； ⑶求异面直线PA与MN所成角的大小.

12.　　 (94上海)如图，在梯形ABCD中，AD∥BC，∠ABC＝90°,AB＝a,AD＝3a,且∠ADC＝arcsin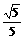,又PA⊥平面ABCD，PA＝a,求： ⑴二面角P－CD－A的大小(用反三角函数表示)； ⑵点A到平面PBC的距离.

11.　　 (93上海)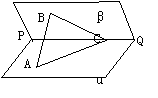如图，已知二面角α－PQ－β为60°，点A和点B分别在平面α和β上，点C在PQ上，∠ACP＝∠BCP＝30°，CA＝CB＝a ⑴求证：AB⊥PQ； ⑵求点B到平面α的距离； ⑶设R是线段CA上一点，直线BR与平面α所成角的大小为45°，求线段CR的长.

10.　　 已知平面α和不在这个平面内的直线a都垂直于平面β，求证：a∥α(92三南)

9.　　　 (92(26)10分)已知:两条异面直线a、b所成的角为θ，它们的公垂线段AA₁的长度为d，在直线a、b上分别取点E、F，设A₁E＝m，AF＝n，求证:EF＝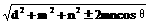

8.　　　 (91上海)如图，设△ABC和△DBC所在的两个平面互相垂直，且AB＝BC＝BD，∠CBA＝∠DBC＝120°，求： ⑴AD的连线与平面BCD所成的角； ⑵AD得连线与直线BC所成的角； ⑶二面角A－BD－C的大小

7.　　　 (91(23)10分)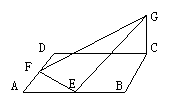已知ABCD是边长为4的正方形，E、F分别是AB、AD的中点，GC垂直于ABCD所在平面，且GC＝2，求点B到平面EFG的距离.

6.　　　 (90上海)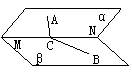如图，平面α、β相交于直线MN，点A在平面α上，点B在平面β上，点C在直线MN上，∠ACM＝∠BCN＝45°.二面角A－MN－B的大小为60°,AC＝1.求： ⑴点A到平面β的距离； ⑵二面角A－BC－M的大小(用反三角函数表示)

5.　　　 (90广东)在三棱锥S－ABC中，SA⊥地面ABC，AB⊥BC，DE垂直平分SC，且分别交AC、SC于点D、E，又SA＝AB＝a，BC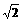＝a(同上题图)，求证：SC⊥面BDE.

4.　　　 (90(23)8分)如图，在三棱锥S－ABC中，SA⊥底面ABC，AB⊥BC，DE垂直平分SC，且分别交AC、SC于点D、E，又SA＝AB，SB＝BC，求以BD为棱，以BDE与BDC为面的二面角的度数.